Gujarat Board GSEB Solutions Class 8 Maths Chapter 4 પ્રાયોગિક ભૂમિતિ InText Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 4 પ્રાયોગિક ભૂમિતિ InText Questions
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબ 58)
અર્ષદ પાસે ચતુષ્કોણ ABCDના પાંચ માપ આ મુજબ છે; AB = 5 સેમી, ∠A = 50°, AC = 4 સેમી, BD = 5 સેમી અને AD = 6 સેમી, તો શું એક નિશ્ચિત ચતુષ્કોણ રચી શકાશે? તમારા જવાબનું કારણ આપો.
ઉત્તરઃ
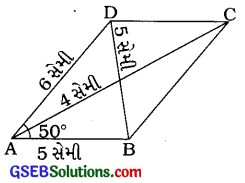
ના, અહીં આપેલાં માપ વડે ચતુષ્કોણ ABCD રચી ન શકાય. આપેલાં માપ પૂરતાં નથી. જો BC અથવા DCનું માપ આપ્યું હોય, તો જ છે ચતુષ્કોણ ABCD રચી શકાય.
વિચારો, ચર્ચા કરો અને લખો (પાઠ્યપુસ્તક પાન નંબ 60)
પ્રશ્ન (i).
આપણે જોયું કે ચતુષ્કોણનાં પાંચ માપ એક નિશ્ચિત ચતુષ્કોણ નિર્ધારિત કરે છે. શું તમે કહી શકશો કે ચતુષ્કોણનાં કોઈ પણ પાંચ માપ દ્વારા આ રીતે નિશ્ચિત ચતુષ્કોણ નિર્ધારિત થશે?
ઉત્તરઃ
ના, ગમે તે પાંચ માપ વડે માગ્યા મુજબનો ચતુષ્કોણ રચી ન શકાય. ખરેખર તો, ચતુષ્કોણ રચવા માટે ચોક્કસ જોડાણવાળાં પાંચ માપ હોવા જરૂરી છે. જેવાં કે –
- ચાર બાજુઓ અને કોઈ એક વિકર્ણ અથવા
- ત્રણ બાજુઓ અને બંને વિકર્ણ અથવા
- બે પાસપાસેની બાજુઓ અને ત્રણ ખૂણા અથવા
- ત્રણ બાજુઓ અને તેને સમાવતા બે ખૂણા અથવા
- કેટલાક ખાસ ગુણધર્મો આપેલા હોય.
![]()
પ્રશ્ન (ii).
શું તમે સમાંતરબાજુ ચતુષ્કોણ BATs એવો દોરી શકો કે જ્યાં BA = 5 સેમી, AT = 8 સેમી અને As = 6.5 સેમી હોય? શા માટે?
ઉત્તરઃ
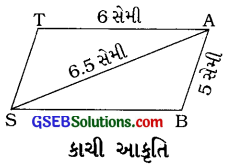
અહીં સમાંતરબાજુ ચતુષ્કોણ BATS રચવા માટે BA = 5 સેમી, AT = 6 સેમી અને AS = 6.5 સેમી માપ આપ્યાં છે. સમાંતરબાજુ ચતુષ્કોણ BATS દર્શાવતી કાચી આકૃતિ દોરીએ. સમાંતરબાજુ ચતુષ્કોણમાં સામસામેની બાજુઓનાં માપ સરખાં હોય છે. તેથી ST = AB = 5 સેમી અને SB = AT = 6 સેમી હોય.
પહેલાં Δ ASB જ્યાં SB = 6 સેમી, AB = 5 સેમી અને AS = 6.5 સેમીથી દોરી શકાય. તે પછી Δ ATS જ્યાં AT = 6 સેમી, ST = 5 સેમી વડે Δ ATS દોરી શકાય.
આમ, આપેલ માપ પરથી સમાંતરબાજુ ચતુષ્કોણ BATS દોરી શકાય છે.
પ્રશ્ન (iii).
શું તમે સમબાજુ ચતુષ્કોણ ZEAL એવો દોરી શકો કે જ્યાં ZE = 3.5 સેમી, વિકર્ણ EL = 5 સેમી હોય? શા માટે?
ઉત્તરઃ
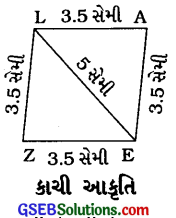
અહીં સમબાજુ ચતુષ્કોણ ZEAL રચવા માટે ZE = 3.5 સેમી અને ZE = 3.5 સેમી અને EL = 5 સેમી માપ આપ્યાં છે. સમબાજુ ચતુષ્કોણની ચારે બાજુઓનાં માપ સરખાં છે હોય. અહીં ZE = 3.5 સેમી છે, તેથી EA = 3.5 સેમી, AL = 3.5 સેમી અને LZ = 3.5 સેમી હોય. વળી એક વિકર્ણનું માપ EL = 5 સેમી આપેલ છે. કાચી આકૃતિ આમ,
સમબાજુ ચતુષ્કોણ રચવા પાંચ જરૂરી માપ જાણીએ છીએ. હા, તેથી અહીં આ સમબાજુ ચતુષ્કોણ રચી શકાય છે.
પ્રશ્ન (iv).
એક વિદ્યાર્થીએ ચતુષ્કોણ PLAY દોરવા પ્રયત્ન કર્યો, જ્યાં PL = 3 સેમી, LA = 4 સેમી, AY = 4.5 સેમી, PY = 2 સેમી અને LY = 6 સેમી હોય, પરંતુ તે દોરી ન શક્યો. શું કારણ હોય? (સૂચનઃ કાચી આકૃતિ દોરી ચર્ચા કરો.)
ઉત્તરઃ
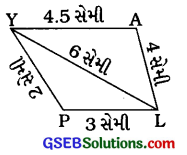
અહીં ચતુષ્કોણ PLAY રચવા માટે PL = 3 સેમી, LA = 4 સેમી, AY = 4.5 સેમી, PY = 2 સેમી અને LY = 6 સેમી માપ આપ્યાં છે. કાચી આકૃતિ પરથી ચતુષ્કોણ રચી શકાય તેવું લાગે છે.
પણ ΔPLYની બાજુઓનાં માપ જોતાં
PL + PY = 3 સેમી + 2 સેમી = 5 સેમી જ્યારે YL = 6 સેમી છે.
કોઈ પણ ત્રિકોણમાં બે બાજુઓનાં માપનો સરવાળો ત્રીજી બાજુ કરતાં વધારે હોય જ. તેથી આ ચતુષ્કોણ માટે બિંદુ P અથવા Yનું ચોક્કસ સ્થાન ન મળતાં ચતુષ્કોણ રચી શકાતો નથી.
![]()
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબ 62)
પ્રશ્ન 1.
શું ઉપરના ઉદાહરણમાં આપણે પહેલા ΔABD દોરી પછી ચોથું બિંદુ C શોધીને, ચતુષ્કોણ દોરી શકીએ?
ઉત્તરઃ
અહીં આપેલાં માપ પરથી ચતુષ્કોણ રચી ન શકાય.
કારણઃ
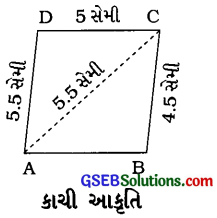
અહીં ABનું માપ આપ્યું નથી. ΔACDનાં ત્રણે માપ આપ્યાં છે તે પરથી ΔACD રચી શકાય. હવે ΔABC માટે BCનું માપ આપ્યું છે પણ ABનું માપ આપ્યું નથી. તેથી બિંદુ Bનું સ્થાન નક્કી થઈ શકતું નથી.
આમ, □ ABCD આપેલાં માપ પરથી રચી ન શકાય.
પ્રશ્ન 2.
શું તમે ચતુષ્કોણ PQRS એવો રચી શકો જ્યાં PQ = 3 સેમી, RS= 3 સેમી, PS = 7.5 સેમી, PR = 8 સેમી અને SQ= 4 સેમી હોય? તમારા જવાબને ચકાસો.
ઉત્તરઃ
અહીં આપેલાં માપ પરથી □ PQRS રચી ન શકાય.
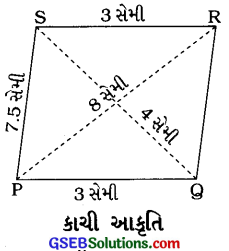
કારણ:
Δ PQSનાં માપ PQ = 3 સેમી, SQ = 4 સેમી અને PS = 7.5 છે.
અહીં PO + SQ ≯ PS
ત્રિકોણની બે બાજુઓના માપનો સરવાળો ત્રીજી બાજુના માપ કરતાં વધુ થતો નથી.
∴ ΔPQS રચી ન શકાય. તેથી □ PQRS રચી ન શકાય.
![]()
વિચારો, ચર્ચા કરો અને લખો : (પાઠ્યપુસ્તક પાન નંબ 64)
પ્રશ્ન 1.
જો આપણી પાસે ∠M એ 75°ને બદલે 100° હોય, તો શું તમે ઉપરનો ચતુષ્કોણ MIST રચી શકો?
ઉત્તરઃ
હા, ચતુષ્કોણ MISTમાં ∠Mનું માપ 75°ને બદલે 100° આપ્યું હોય,
તોપણ ચતુષ્કોણ MIST રચી શકાય.
અહીં જો ચતુષ્કોણ MIST માટે MI = 3.5 સેમી, IS = 6.5 સેમી, ∠M = 75°, ∠I = 105° અને ∠S = 100° માપથી રચી શકાય, તો માપ ∠M = 100° લેતાં પણ આ ચતુષ્કોણ રચી શકાય. માત્ર ચતુષ્કોણ મોટો બને એટલું જ.
પ્રશ્ન 2.
જો PL = 6 સેમી, LA = 9.5 સેમી, ∠P = 75°, ∠L = 150° અને ∠A = 140° હોય, તો તમે ચતુષ્કોણ PLAN રચી શકો? (સૂચનઃ ખૂણાના સરવાળાની લાક્ષણિકતા યાદ કરો.)
ઉત્તરઃ
અહીં ચતુષ્કોણ PLAN માટે PL = 6 સેમી, LA = 9.5 સેમી, ∠P = 75°, ∠L = 150° અને ∠A = 140° માપ આપ્યાં છે.
આ ચતુષ્કોણ માટેના ખૂણાઓનાં માપનો સરવાળો ચકાસીએ.
m∠P + m∠L + m∠A + m∠N = 75° + 150° + 140° + m∠N
= 365° + m∠N > 360°
આમ, ચતુષ્કોણના ચારેય ખૂણાઓનાં માપનો સરવાળો 360° થી વધારે છે.
∴ □ PLAN રચી ન શકાય.
પ્રશ્ન 3.
સમાંતરબાજુ ચતુષ્કોણમાં પાસપાસેની બાજુઓ(Adjacent sides)ની લંબાઈ જાણતાં હોઈએ તોપણ ઉપરના ઉદાહરણની રચના માટે ખૂણાનાં માપની જરૂર રહેશે?
ઉત્તરઃ
સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુઓ સરખી અને સમાંતર હોય છે. અહીં સમાંતરબાજુ ચતુષ્કોણની પાસપાસેની બાજુઓનાં માપ જાણીએ છીએ. તેથી ચતુષ્કોણ રચવા માટે ખૂણાઓનાં માપ જાણવા જરૂરી નથી. જો કોઈ પણ એક વિકર્ણનું માપ જાણતા હોઈએ તો પણ ચતુષ્કોણ દોરી શકાય.
![]()
આટલું કરો : (પાઠ્યપુસ્તક પાન નંબ 67)
પ્રશ્ન 1.
જો તમે માત્ર PQ અને QRની લંબાઈ જાણતા હશો તો લંબચોરસ PQRS કઈ રીતે રચશો?
ઉત્તરઃ
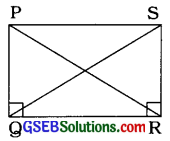
લંબચોરસના બધા ખૂણાઓનાં માપ 90° હોય છે. વળી PQ = Rs હોય.
PQ, ∠Q = 90° અને QRના માપ પરથી ΔPOR રચાય.
QR, ∠R = 90° અને RSના માપ પરથી ΔQRS રચાય.
આમ, લંબચોરસ PQRS રચી શકાય.
પ્રશ્ન 2.
જો આકૃતિમાં AY = 8 સેમી, EY = 4 સેમી અને SY = 6 સેમી હોય, તો પતંગ EASYની રચના કરો. પતંગની કઈ લાક્ષણિકતા તમે રચના દરમિયાન ઉપયોગમાં લેશો?
ઉત્તરઃ
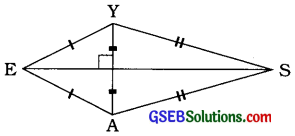
પતંગમાં વિકર્ણો પરસ્પર કાટખૂણે છેદે છે.
પતંગમાં પાસપાસેની બાજુઓની એક-એક જોડ સમાન હોય છે.
રચના કરતાં આપેલાં માપ પ્રમાણે E બિંદુનું સ્થાન નક્કી કરી શકાતું નથી.
∴ પતંગ EASY રચી શકાતો નથી. (∵ ΔEYA માટે બે બાજુઓનાં માપનો સરવાળો (4 + 4) એ ત્રીજી બાજુ (8)ના માપ કરતાં વધારે નથી.)