GSEB Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ Ex 6.4

Gujarat Board GSEB Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ Ex 6.4 Textbook Exercise Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 6 વર્ગ અને વર્ગમૂળ Ex 6.4

1.નીચે આપેલી સંખ્યાઓનું ભાગાકારની રીતે વર્ગમૂળ શોધોઃ

પ્રશ્ન (i).
2304
ઉત્તરઃ

પ્રશ્ન (ii).
4489
ઉત્તરઃ

પ્રશ્ન (iii).
3481
ઉત્તરઃ

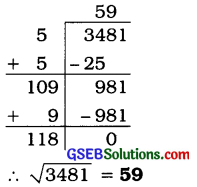
પ્રશ્ન (iv).
529
ઉત્તરઃ

પ્રશ્ન (v).
3249
ઉત્તરઃ

પ્રશ્ન (vi).
1369
ઉત્તરઃ

પ્રશ્ન (vii).
5776
ઉત્તરઃ

પ્રશ્ન (viii).
7921
ઉત્તરઃ

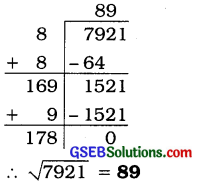
પ્રશ્ન (ix).
576
ઉત્તરઃ

પ્રશ્ન (x).
1024
ઉત્તરઃ

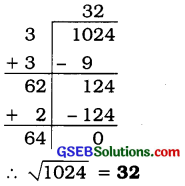
પ્રશ્ન (xi).
3136
ઉત્તરઃ

પ્રશ્ન (xii).
900
ઉત્તરઃ

2. નીચે આપેલી સંખ્યાના વર્ગમૂળ તરીકે આવતી સંખ્યામાં કેટલા અંકો હશે તે જણાવો (કોઈ ગણતરી કર્યા વગર જણાવો.)

પ્રશ્ન (i).
64
ઉત્તરઃ
64માં અંકોની સંખ્યા = 2
∴ n = 2 જે બેકી સંખ્યા છે.
∴ 64ના વર્ગમૂળની સંખ્યામાં અંકોની સંખ્યા = \(\frac{n}{2}=\frac{2}{2}\) = 1

પ્રશ્ન (ii).
144
ઉત્તરઃ
144માં અંકોની સંખ્યા = 3
∴ n = 3 જે એકી સંખ્યા છે.
∴ 144ના વર્ગમૂળની સંખ્યામાં અંકોની સંખ્યા = \(\frac{n+1}{2}\)
= \(\frac{3+1}{2}\)
= \(\frac {4}{2}\)
= 2

પ્રશ્ન (iii).
4489
ઉત્તરઃ
4489માં અંકોની સંખ્યા = 4
∴ n = 4 જે બેકી સંખ્યા છે.
∴ 4489ના વર્ગમૂળની સંખ્યામાં અંકોની સંખ્યા = \(\frac{n}{2}=\frac{4}{2}\) = 2

પ્રશ્ન (iv).
27225
ઉત્તરઃ
27225માં અંકોની સંખ્યા = 5
∴ n = 5 જે એકી સંખ્યા છે.
∴ 27225ના વર્ગમૂળની સંખ્યામાં અંકોની સંખ્યા = \(\frac{n+1}{2}\)
= \(\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

પ્રશ્ન (v).
390625
ઉત્તરઃ
390625માં અંકોની સંખ્યા = 6
∴ n = 6 જે બેકી સંખ્યા છે.
∴ 390625ના વર્ગમૂળની સંખ્યામાં અંકોની સંખ્યા = \(\frac{n}{2}=\frac{6}{2}\) = 3

3. નીચે આપેલ દશાંશ સંખ્યાઓનું વર્ગમૂળ શોધોઃ

પ્રશ્ન (i).
2.56
ઉત્તરઃ
2.56

2.56માં દશાંશ-સ્થળ જ.બા.થી બે અંકો આગળ છે.
∴ વર્ગમૂળમાં દશાંશ-સ્થળ જ.બા.થી એક અંક આગળ આવે.

પ્રશ્ન (ii) .
7.29
ઉત્તરઃ
7.29

7.29માં દશાંશ-સ્થળ જ.બા.થી બે અંકો આગળ છે.
∴ વર્ગમૂળમાં દશાંશ-સ્થળ જ.બા.થી એક અંક આગળ આવે.

પ્રશ્ન (iii).
51.84
ઉત્તરઃ
51.84

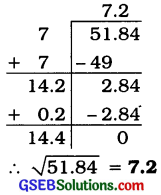
51.84માં દશાંશ-સ્થળ જ.બા.થી બે અંકો આગળ છે.
∴ વર્ગમૂળમાં દશાંશ-સ્થળ જ.બા.થી એક અંક આગળ આવે.

પ્રશ્ન (iv).
42.25
ઉત્તરઃ
42.25

42.25માં દશાંશ-સ્થળ જ.બા.થી બે અંકો આગળ છે.
∴ વર્ગમૂળમાં દશાંશ-સ્થળ જ.બા.થી એક અંક આગળ આવે.

પ્રશ્ન (v).
31.86
ઉત્તરઃ
31.36

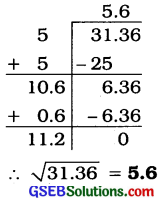
31.36માં દશાંશ-સ્થળ જબા થી બે અંકો આગળ છે.
∴ વર્ગમૂળમાં દશાંશ-સ્થળ જ.બા.થી એક અંક આગળ આવે.

4. નીચે આપેલી સંખ્યાઓ માટે એવી નાનામાં નાની સંખ્યા શોધો કે જેની આપેલ સંખ્યામાંથી બાદબાકી કરતાં મળતી નવી સંખ્યા પૂર્ણવર્ગ હોય. ઉપરાંત આ નવી સંખ્યાનું વર્ગમૂળ પણ શોધોઃ

પ્રશ્ન (i).
402
ઉત્તરઃ
402

20 ભાગાકારની રીતે 402નું વર્ગમૂળ શોધતાં 2 શેષ વધે છે.
∴ 402માંથી 2 બાદ કરતાં મળતી સંખ્યા (400) એ પૂર્ણવર્ગ સંખ્યા હોય.
આમ, 402 – 2 = 400 અને \(\sqrt{400}\) = 20
402માંથી નાનામાં નાની સંખ્યા 2 બાદ કરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (ii).
1989
ઉત્તરઃ
1989

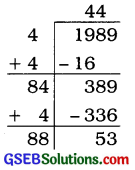
ભાગાકારની રીતે 1989નું વર્ગમૂળ શોધતાં 53 શેષ વધે છે.
∴ 1989માંથી 53 બાદ કરતાં મળતી સંખ્યા (1936) એ પૂર્ણવર્ગ સંખ્યા હોય.
આમ, 1989 – 53 = 1936 અને
\(\sqrt{1936}\) = 44
1989માંથી નાનામાં નાની સંખ્યા 53 બાદ કરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (iii).
3250
ઉત્તરઃ
3250

ભાગાકારની રીતે 3250નું વર્ગમૂળ શોધતાં 1 શેષ વધે છે.
∴ 3250માંથી 1 બાદ કરતાં મળતી સંખ્યા (3249) એ પૂર્ણવર્ગ સંખ્યા હોય.
આમ, 3250 – 1 = 3249 અને
\(\sqrt{3249}\) = 57
3250માંથી નાનામાં નાની સંખ્યા 1 બાદ કરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (iv).
825
ઉત્તરઃ
825

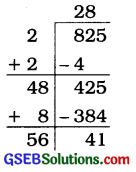
ભાગાકારની રીતે 825નું વર્ગમૂળ શોધતાં 41 શેષ વધે છે.
∴ 825માંથી 41 બાદ કરતાં મળતી સંખ્યા (784) એ પૂર્ણવર્ગ સંખ્યા હોય.
આમ, 825 – 41 = 784 અને \(\sqrt{784}\) = 28
825માંથી નાનામાં નાની સંખ્યા 41 બાદ કરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (v).
4000
ઉત્તરઃ
4000

ભાગાકારની રીતે 4000નું વર્ગમૂળ શોધતાં 31 શેષ વધે છે.
∴ 4000માંથી 31 બાદ કરતાં મળતી સંખ્યા (3969) એ પૂર્ણવર્ગ સંખ્યા હોય.
આમ, 4000 – 31 = 3969 અને
\(\sqrt{3969}\) = 63
4000માંથી નાનામાં નાની સંખ્યા 31 બાદ કરતાં પૂર્ણવર્ગ સંખ્યા મળે.

5. નીચે આપેલી સંખ્યાઓ માટે એવી નાનામાં નાની સંખ્યા શોધો કે જેનો સરવાળો આપેલ સંખ્યા સાથે કરવાથી મળતી નવી સંખ્યા પૂર્ણવર્ગ હોય. ઉપરાંત આ નવી સંખ્યાનું વર્ગમૂળ પણ શોધોઃ

પ્રશ્ન (i).
525
ઉત્તરઃ
525

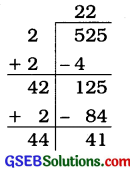
ભાગાકારની રીતે 525નું વર્ગમૂળ શોધતાં 41 શેષ વધે છે.
હવે, 525 > 22²
22ની પછીની સંખ્યા 23 છે. 23² = 529
આમ, ઉમેરવાની સંખ્યા = 23² – 525 = 529 – 525 = 4
હવે, 525 + 4 = 529 અને \(\sqrt{529}\) = 23
આમ, 525માં નાનામાં નાની સંખ્યા 4 ઉમેરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (ii).
1750
ઉત્તરઃ
1750

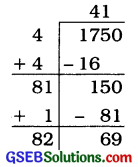
ભાગાકારની રીતે 1750નું વર્ગમૂળ શોધતાં 69 શેષ વધે છે.
હવે, 1750 > 41²
41ની પછીની સંખ્યા 42 છે. 42² = 1764
આમ, ઉમેરવાની સંખ્યા = 42² – 1750
= 1764 – 1750
= 14
હવે, 1750 + 14 = 1764 અને
\(\sqrt{1764}\) = 42
આમ, 1750માં નાનામાં નાની સંખ્યા 14 ઉમેરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (iii).
252
ઉત્તરઃ
252

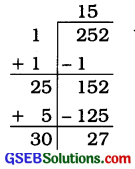
ભાગાકારની રીતે 252નું વર્ગમૂળ શોધતાં 27 શેષ વધે છે.
હવે, 252 > 15²
15ની પછીની સંખ્યા 16 છે. 16² = 256
આમ, ઉમેરવાની સંખ્યા = 16² – 252
= 256 – 252
= 4
હવે, 252 + 4 = 256 અને \(\sqrt{256}\) = 16
આમ, 252માં નાનામાં નાની સંખ્યા 4 ઉમેરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (iv).
1825
ઉત્તરઃ
1825

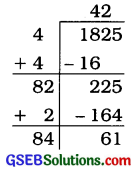
ભાગાકારની રીતે 1825નું વર્ગમૂળ શોધતાં 61 શેષ વધે છે.
હવે, 1825 > 42²
42ની પછીની સંખ્યા 43 છે. 43² = 1849
આમ, ઉમેરવાની સંખ્યા = 43² – 1825
= 1849 – 1825
= 24
હવે, 1825 + 24 = 1849 અને
\(\sqrt{1849}\) = 43
આમ, 1825માં નાનામાં નાની સંખ્યા 24 ઉમેરતાં પૂર્ણવર્ગ સંખ્યા મળે.

પ્રશ્ન (v).
6412
ઉત્તરઃ
6412

ભાગાકારની રીતે 6412નું વર્ગમૂળ શોધતાં 12 શેષ વધે છે.
હવે, 6412 > 80²
80ની પછીની સંખ્યા 81 છે. 81² = 6561
આમ, ઉમેરવાની સંખ્યા = 81² – 6412
= 6561 – 6412
= 149
હવે, 6412 + 149 = 6561 અને
\(\sqrt{6561}\) = 81
આમ, 6412માં નાનામાં નાની સંખ્યા 149 ઉમેરતાં પૂર્ણવર્ગ સંખ્યા મળે.

6. 441 મીટર ક્ષેત્રફળવાળા ચોરસની બાજુનું માપ શોધો.
ઉત્તરઃ
ધારો કે, ચોરસની બાજુની લંબાઈ x મીટર છે.
હવે, ચોરસનું ક્ષેત્રફળ = લંબાઈ × લંબાઈ
ચોરસનું ક્ષેત્રફળ = x × x મીટર² = x² મીટર²
હવે, અહીં ચોરસનું ક્ષેત્રફળ 441 મીટર² આપેલ છે.
∴ x² = 441
∴x = \(\sqrt{441}\)
∴ x = 21 મીટર

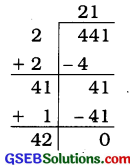
આમ, ચોરસની બાજુનું માપ 21 મીટર છે.

7.કાટકોણ ત્રિકોણ ABCમાં, ∠B = 90° છેઃ

પ્રશ્ન (i).
જો AB = 6 સેમી, BC = 8 સેમી, તો AC શોધો.
ઉત્તરઃ
કાટકોણ ત્રિકોણમાં કાટખૂણાની સામેની બાજુને કર્ણ કહે છે. કાટકોણ ત્રિકોણમાં કર્ણ સૌથી મોટી બાજુ હોય.
કાટકોણ ત્રિકોણ માટે = (કર્ણ)² = (એક બાજુ)² + (બીજી બાજુ)²
અહીં, m∠B = 90°, AB = 6 સેમી; BC = 8 સેમી અને AC = ?

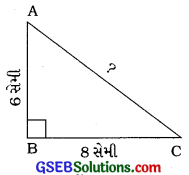
ΔABCમાં AC કર્ણ છે.
AC² = AB² + BC²
= (6)² + (8)²
= 36 + 64
= 100
∴ AC = \(\sqrt{100}\) = 10 સેમી

પ્રશ્ન (ii).
જો AC = 13 સેમી, BC = 5 સેમી, તો AB શોધો.
ઉત્તરઃ
અહીં, m∠B = 90°, AC = 3 સેમી; BC = 5 સેમી અને AB = ?
ΔABCમાં AC કર્ણ છે.

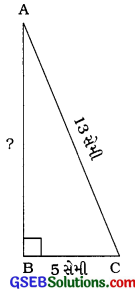
AC² = AB² + BC²
∴ (13)² = AB² + (5)²
∴ 169 = AB² + 25
∴ AB² = 169 – 25
= 144
∴ AB = \(\sqrt{144}\)
= 12 સેમી

8. એક માળી પાસે 1000 છોડ છે. તે આ છોડને એવી રીતે રોપવા માગે છે કે બગીચામાં હાર અને સ્તંભોની સંખ્યા સમાન મળે, તો માળીને તેના માટે હજુ ઓછામાં ઓછા કેટલા છોડ વધુ જોઈએ?
ઉત્તરઃ
અહીં ઊભા સ્તંભમાં અને આડી હારમાં સરખી સંખ્યામાં છોડ રોપવાના છે.
ધારો કે, ઊભા સ્તંભમાં x છોડ રોપે છે. તેથી આડી હારમાં પણ x છોડ રોપે છે.
કુલ જરૂરી છોડ = x × x = x²
પરંતુ માળી પાસે કુલ 1000 છોડ છે.
∴ x² = 1000
∴ x = \(\sqrt{1000}\)
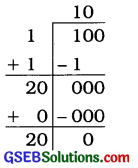
હવે, 1000 એ પૂર્ણ સંખ્યા નથી. (જઓ 39 શેષ)
(31)² < 1000

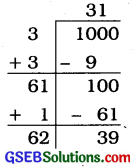
31થી મોટી સંખ્યા 32 છે. 32² = 1024
∴ જરૂરી બીજા છોડ = 1024 – 1000 = 24
આમ, હારમાં અને સ્તંભમાં સરખી સંખ્યામાં છોડ રોપવા બીજા 24 છોડ જોઈશે.

9. એક નિશાળમાં 500 વિદ્યાર્થીઓ છે. પી.ટી.ની કવાયત કરવા માટે તમામ વિદ્યાર્થીઓને એવી રીતે ઊભા રાખ્યા છે કે જેથી હાર અને સ્તંભોની સંખ્યા સમાન રહે, તો નિશાળના કેટલા વિદ્યાર્થીઓ આ ગોઠવણી કરવાથી બહાર રહેશે?
ઉત્તરઃ
ધારો કે, આડી હારમાં x વિદ્યાર્થી ઊભા છે, તો ઊભા સ્તંભમાં પણ x વિદ્યાર્થી ઊભા છે.
∴ આડી હાર અને ઊભા સ્તંભમાંના કુલ વિદ્યાર્થી = x × x = x²
વિદ્યાર્થીઓની સંખ્યા = 500
∴ x² = 500
∴ x = \(\sqrt{500}\)
500 એ પૂર્ણવર્ગ સંખ્યા નથી. (જુઓ શેષ 16)
∴ 500 > 22²
∴ 500 > 484
500 – 484 = 16 વિદ્યાર્થી બાકી રહેશે.
આમ, આડી હારમાં અને ઊભા સ્તંભમાં સરખા વિદ્યાર્થી રાખતાં 16 વિદ્યાર્થી બહાર રહેશે.