GSEB Solutions Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.2

Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method?

1. 64
2. 512
3. 10648
4. 27000
5. 15625
6. 13824
7. 110592
8. 46656
9. 175616
10. 91125

Solution:
1. By prime factorisation, we have

Thus, cube root of 64 is 4.

2. By prime factorisation, we have


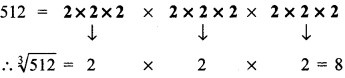
Thus, cube root of 512 is 8

3. By prime factorisation, we have

Thus, the cube root of 10648 is 22.

4. By prime factorisation, we have

Thus, the cube root of 27000 is 30.

5. By prime factorisation, we have

Thus, cube root of 15625 is 25.

6. By prime factorisation, we have
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{13824}\) = 2 × 2 × 2 × 3

Thus, the cube root of 13824 is 24.

7. By prime factorisation,
we have

110592 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{110592}\) = 2 × 2 × 2 × 2 × 3 = 48
Thus, the cube root of 110592 is 48.

8. By the prime factorisation,
we have
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
∴ \(\sqrt[3]{46656}\) = 2 × 2 × 3 × 3 = 36
Thus, the cube root of 46656 is 36.

9. By prime factorisation,
we have
175616 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 × 7 = 2 × 2 × 2 × 7 = 56
Thus, the cube root of 175616 is 56.

10. By prime factorisation,
we have
91125 = 3 × 3 × 3 × 3 × 3 × 3 × 5 × 5 × 5
∴ \(\sqrt[3]{91125}\) = 3 × 3 × 5 = 45
Thus, the cube root of 91125 is 45

Question 2.
State true or false.

1. Cube of any odd number is even.
2. A perfect cube does not end with two zeros.
3. If square of a number ends with 5, then its cube ends with 25.
4. There is no perfect cube which ends with 8.
5. The cube of a two digit number may be a three digit number.
6. The cube of a two digit number may have seven or more digits.
7. The cube of a single digit number may be a single digit number.

Solution:

1. False
2. True
3. False
4. False
5. False
6. False
7. True

Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768?
Solution:
1. Separating the given number (1331) into two groups:
1331 → 1 and 331
∵ 331 ends in 1.
∴ Units digit of the cube root = 1
∵ 1³ = 1 and \(\sqrt[3]{1}\) = 1
∴ Tens digit of the cube root = 1
∴ \(\sqrt[3]{1331}\) = 11

2. Separating the given number (4913) in two groups:
4913 → 4 and 913

Units digits:
∵ Units digit in 913 is 3.
∴ Units digit of the cube root = 7
[7³ = 343; which ends in 3]

Tens digit:
∵ 1³ = 1, 2³ = 8
and 1 < 4 < 8
i.e; 1³ < 4 < 2³
∴ The ten’s digit of the cube root is 1.
∴ \(\sqrt[3]{4913}\) = 17

3. Separating 12167 in two groups:
12167 → 12 and 167

Units digit:
∵ 167 is ending in 7 and cube of a number ending in 3 ends in 7.
∴ The units digit of the cube root = 3

Tens digit:
∵ 3³ = 27 and 4³ = 64
Alao, 27 < 32 < 64
or 3³ < 32 < 4³
∴ The tens digit of the cube root = 3.
Thus, \(\sqrt[3]{32768}\) = 32