Gujarat Board GSEB Solutions Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry Ex 5.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry Ex 5.2
Question 1.
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Solution:
Two lines are said to be parallel if they are equidistant from others and they do not have any point of intersection. Let us suppose a line l and a point P, not l, then by Playfair’s axiom (which is equivalent to the fifth postulate) a unique m line can pass through point P which is parallel to l.
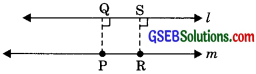
The distance between l and m is PQ, which is perpendicular from the point P to line l. Again let RS be perpendicular to l from any point R on m, therefore PQ = RS. Hence the distance between two lines is equal, thus the two lines are equidistant everywhere from one another.
![]()
Question 2.
Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Solution:
According to the fifth postulate, when line n intersects two lines l and m at two distinct points (when two lines are not parallel) then the sum of two interior angles is always less than two right angles if both lines produced indefinitely meet on that side, i.e.,
If ∠1 + ∠2 <180° or ∠3 + ∠4 > 180°; lines l and m will meet on the left side of linen.
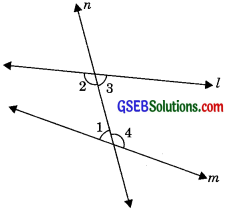
If ∠1 + ∠2 = 180° or, ∠3 + ∠4 = 180°, then l || m.