Gujarat Board GSEB Solutions Class 9 Maths Chapter 7 Triangles Ex 7.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 7 Triangles Ex 7.5
Question 1.
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
Solution:
Draw perpendicular bisector of any two sides of ΔABC. The point of intersection of these perpendicular bisectors is equidistant from all the vertices of Hence point O will be the centre of the circle which passes through all vertices.
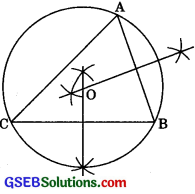
Question 2.
In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Solution:
The draw angle bisector of any two angles of a triangle. Where the point of intersection of these angle bisectors would be equidistant from all the three sides of the triangle. Thus, point O is the in centre of the triangle.
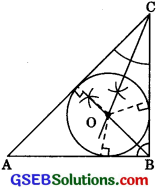
Question 3.
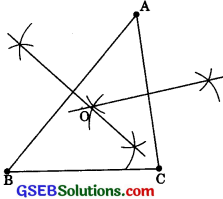
In a huge park, people are concentrated at three points (See figure)
A: where there are different slides and swings for children.

B: near which a man-made lake is situated.
C: which is near to a large parking and exit. Where should an ice-cream parlour be set up so that the maximum number of persons can approach it?
(Hint: the parlour should be equidistant from A, B and C)
Solution:
If ice-cream parlour is situated on the circumcentre of the circle, then the maximum number of people will reach. It will be equidistant from each vertex A, B and C.
![]()
Question 4.
Complete the hexagonal and star shaped Rangolies (See figure (i) and (ii)) by filling them with as many equilateral triangles of side 1 cm as you can. Count the number of triangles in each case. Which has more triangles?
Solution:
(i) Area of ΔOAB = \(\frac{\sqrt{3}}{4}\) side2 =\(\frac{\sqrt{3}}{4}\) x 52
\(\frac{\sqrt{3} \times 25}{4}\)
Area of hexagonal shaped Rangoli = \(\frac{6 \times 25 \sqrt{3}}{4}\) = \(\frac{75}{2} \sqrt{3}\)
Area of an equilateral triangle of side 1 cm
= \(\frac{\sqrt{3}}{4}\) x 12 = \(\frac{\sqrt{3}}{4}\) cm2
No. of equilateral triangles of side 1 cm formed in hexagonal Rangoli

(ii) Star shaped Rangoli has 12 equilateral triangles of side 5 cm each.
∴ Area of star shaped Rangoli = 12 x \(\frac{\sqrt{3}}{4}\) x 52
= 12 x \(\frac{\sqrt{3}}{4}\) x 25 = 75 \(\sqrt{3}\)
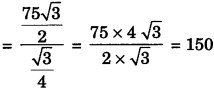
No. of equilateral triangles of side 1 cm formed in stare shaped Rangoli
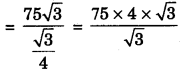
= 75 x 4 = 300
Therefore, star shaped Rangoli has more triangles.
![]()