Gujarat Board GSEB Solutions Class 9 Maths Areas of Parallelograms and Triangles Ex 9.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Areas of Parallelograms and Triangles Ex 9.3
Question 1.
In the figure, E is any point on the median AD of a ΔABC. Show that ar(ΔABE) = ar(ΔACE).
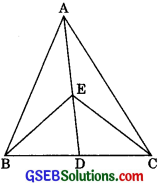
Solution:
Given: E is any point on median AD of a ΔABC. In ΔABC,
∴ AD is a median.
∴ ar(ΔABD) = ar(ΔACD) ………(1)
A median of a triangle divides it into two triangles of equal areas.
In ΔEBC,
∴ ED is a median.
∴ ar(ΔEBD) = ar(ΔECD) ………(2)
A median of a triangle divides it into two triangles of equal areas.
Subtracting (2) from (1), we get
ar(ΔABD) ≅ ar(ΔEBD)
= ar(ΔACD) ≅ ar(ΔECD)
⇒ ar(ΔABE) = ar(ΔACE)
![]()
Question 2.
In a triangle ABC, E is the mid-point of median AD. Show that
ar(ΔBED) = \(\frac {1}{4}\) ar(ΔABC)
Solution:
In ΔABC,
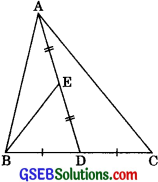
∴ AD is a median.
∴ ar(ΔABD) = ar(ΔACD) = \(\frac {1}{4}\) ar(ΔABC) …….(1)
A median of a triangle divides it into two triangles of equal areas
Similarly, BE is a median in ΔABD,
ar(ΔBED) = \(\frac {1}{2}\) ar(ΔABD)
= \(\frac {1}{2}\) . \(\frac {1}{2}\) ar (ΔABD) [ From (1)]
\(\frac {1}{4}\) ar (ΔABD)
Question 3.
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution:
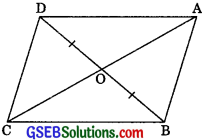
Given: ABCD is a parallelogram whose diagonals AC and BD intersecting at O divide it into four triangles ΔOAB, ΔOBC, ΔOCD and ΔODA.
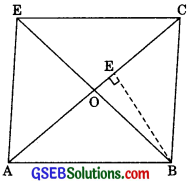
To Prove: ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA)
Construction: Draw BE ⊥ AC
Proof: Now,

= \(\frac {(OC) (BE)}{2}\)
But OA = OC
∴ ar(ΔOAB) = ar(ΔOBC) …….(1)
Similarly,
ar(ΔOBC) = ar(ΔOCD) …….(2)
and, ar(ΔOCD) = ar(ΔODA) …….(3)
From (1), (2) and (3), we get ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA)
![]()
Question 4.
In the figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O. Show that ar(ΔABC) = ar(ΔABD).

Solution:
Line segment CD is bisected by AB at O.
∴ OC = OD
∴ BO is a median of ABCD, and
AO is a median of AACD.
∴ BO is a median of ABCD.
∴ ar(ΔOBC) = ar(ΔOBD) ………..(1)
∴ A median of a triangle divides it into two triangles of equal areas
Similarly, AO is a median of ΔACD.
∴ ar(ΔOAC) = ar(ΔOAD) ……….(2)
Adding (1) and (2), we get
ar(ΔOBC) + ar(ΔOAC)
= ar(ΔOBD) + ar(ΔOAD)
⇒ ar(ΔABC) = ar(ΔABD)
Question 5.
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF) = \(\frac {1}{4}\) ar(ΔABC)
(iii) ar(□BDEF) = \(\frac {1}{2}\) ar(ΔABC)
Solution:
(i) In AABC, F is the mid-point of side AB and E is the mid-point of side AC.
∴ EF || BC
∴ In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side.
⇒ EF || BD ………(1)
Similarly, ED || BF ………(2)
In view of (1) and (2),
□BDEF is a parallelogram.
∴ A quadrilateral is a parallelogram if its opposite sides are parallel.
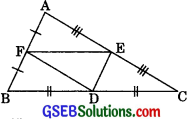
(ii) As in (i), we can prove that
□AFDE and □FDCE are parallelograms,
∴ FD is a diagonal of || gm BDEF.
∴ ar(ΔFBD) = ar(ΔDEF) ……(3)
Similarly, ar(ΔDEF) = ar(ΔFAE) ……(4)
and, ar(ΔDEF) = ar(ΔDCE) ……(5)
From (3), (4) and (5), we have
ar(ΔFBD) = ar(ΔDEF) = ar(ΔFAE) = ar(ΔDCE) ……..(6)
Now, ΔABC is divided into four non-overlapping triangles ΔFBD, ΔDEF, ΔFAE and ΔDCE.
∴ ar(ΔABC) = ar(ΔFBD) + ar(ΔDEF) + ar(ΔFAE) + ar(ΔDCE) = 4 ar(ΔDEF) [From (6)]
⇒ ar(ΔDEF) = \(\frac {1}{4}\) ar(ΔABC) ……..(7)
(iii) ar(□BDEF)
= ar(ΔFBD) + ar(ΔDEF)
= ar(ΔDEF) + ar(ΔDEF) [From (3)] = 2ar(ΔDEF)
= 2. \(\frac {1}{4}\)ar(ΔABC) [From (7)]
= \(\frac {1}{2}\) ar(ΔABC).
![]()
Question 6.
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram
[Hint: From D and B, draw perpendiculars to AC.]
Solution:
Construction: Draw DE ⊥ AC and BF ⊥ AC.
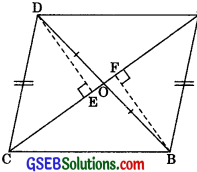
(i) In ΔODE and DOBF,
∠OED = ∠OFB (each 90°)
∠DOE = ∠BOF (Vertically opposite angles)
OB = OB (given)
∴ ΔDOE = ΔBOF (By AAS congruency)
⇒ DE = BF
and OE = OF ……..(1) (CPCT)
Also, ar(ΔDOE) = ar(ΔBOF) ………(2)
Again, in right ΔDEC and ΔBFA,
Hyp. DC = Hyp. BA [Given]
DE = BF (Proved above)
∠DEC = ∠BFA (each 90°)
∴ ΔDEC = ΔBFA | RHS rule
∴ CE = AF ………(3)
Adding eqn. (2) and (4),
ar(ΔDOE) + ar(ΔCDE) = ar(ΔBOF) + ar(ΔABF)
⇒ ar(ΔDOC) – ar(ΔAOB)
(ii) From (i)
ar(ΔDOC) = ar(ΔAOB)
⇒ ar(ΔDOC) + ar(ΔOCB) = ar(ΔAOB) + ar(ΔOCB)
Adding equal areas on both sides
⇒ ar(ΔDCB) = ar(ΔACB)
(ii) In point (iii), ADCB and ΔACB having same area lie on the same base AD, therefore, DA || CB
Adding eqn. (1) and (3), we get
OE = CE = OF + AF
⇒ OC = OA
Also, OB = OD (given)
⇒ ABCD is a parallelogram
(∴ If diagonals of quadrilateral bisect each other, ten it is a parallelogram)
![]()
Question 7.
D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE || BC.
Solution:
Given: D and E are points on side AB and AC respectively of ΔABC, such that ar(ΔDBC) = ar(ΔEBC)
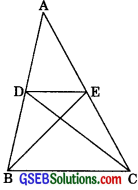
To prove: DE || BC
Proof: ΔDBC and AEBC are on the same base BC and have equal areas.
∴ Their altitudes must be the same.
∴ DE || BC
Question 8.
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar(ΔABE) = ar(ΔACF).
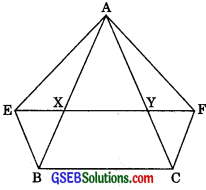
Solution:
XF || BC [Given XY || BC]
and CF || BX [∴ CF || AB (Given)]
∴ □BCFX is a ||gm.
A quadrilateral is a parallelogram I if its opposite sides are parallel
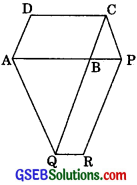
∴ BC = XF
Opposite sides of a parallelogram are equal.
⇒ BC = XY + YF ………(1)
Again,
∴ EY || BC [Given]
and BE || CY [∴ BE || AC (Given)]
∴ ΔBCYE is a parallelogram.
A quadrilateral is a parallelogram I if its opposite sides are parallel.
∴ BC = YE
Opposite sides of a parallelogram are equal.
⇒ BC = XY + XE ………(2)
From (1) and (2),
XY + YF = XY + XE
⇒ YF = XE
⇒ XE = YF ………(3)
∴ ΔAEX and AAYF have equal bases
(∴ XE = YF) on the same line EF and have a common vertex A.
∴ Their altitudes are also the same.
∴ ar(ΔAEX) = ar(ΔAFY) ……..(4)
∴ ΔABEX and ACFY have equal bases (∴ XE = YF) on the same line EF and are between the same parallels EF and BC (∴ XY || BC).
∴ ar(ΔBEX) = ar(ΔCFY) ………(5)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Adding the corresponding sides of (4) and (5), we get
ar(ΔAEX) + ar(ΔBEX) = ar(ΔAFY) + ar(ΔCFY)
⇒ ar(ΔABE) = ar(ΔACF)
![]()
Question 9.
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar(|| gm ABCD) = ar(|| gm PBQR)

[Hint: Join AC and PQ. Now compare ar(ACQ) and ar(APQ)]
Solution:
To Prove: ar(|| gm ABCD) = ar(|| gm PBQR)
Construction: Join AC and PQ
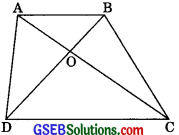
Proof: AC is a diagonal of || gm ABCD
∴ ar(ΔABC) = \(\frac {1}{2}\) ar(||gm ABCD) ……..(1)
PCQ is a diagonal of || gm BQRP
ar(ΔBPQ) = \(\frac {1}{2}\) ar(||gm BQRP) ……..(2)
Also, ar(ΔACQ) = ar(ΔAPQ)
ΔACQ and ΔAPQ are on the same base AQ and between the same. parallels (AQ and CP are equal in area
⇒ ar(ΔACQ) – ar(ΔABQ) = ar(ΔAPQ) – ar(ΔABQ)
Subtracting the same areas from both sides
⇒ ar(ΔABC) = ar(ΔBPQ)
⇒ \(\frac {1}{2}\) ar(|| gm ABCD) = \(\frac {1}{2}\) ar(|| gm PBQR) [From (1) and (2)]
⇒ ar(|| gm ABCD) = ar(|| gm PBQR)
![]()
Question 10.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC)
Solution:
ΔABD and ΔABC are on the same base AB and between the same parallels AB and DC.
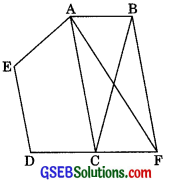
∴ ar(ΔABD) = ar(ΔABC)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
ar(ΔABD) – ar(ΔAOB) = ar(ΔABC) – ar(ΔAOB)
Subtracting the same areas from both sides.
⇒ ar(ΔAOD) = ar(ΔBOC)
Question 11.
In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ΔBCDE)
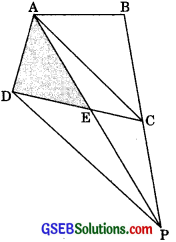
Solution:
(i) ∴ ΔACB and ΔACF are on the same base AC and between the same parallels AC and BF.
[∴ AC || BF (Given)]
∴ ar(ΔACB) = ar(ΔACF)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
(ii) From (i),
ar(ΔACB) = ar(ΔACF)
⇒ ar(ΔACB) + ar(□AEDC) = ar(ΔACF) + ar(□AEDC)
Adding the same areas on both sides.
⇒ ar(ABCDE) = ar(□AEDF)
∴ ar(□AEDF) = ar(ABCDE)
![]()
Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the comers to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:
Let ABCD be the plot of land of the shape of a quadrilateral. Let the portion ADE be taken over by the Gram Panchayat of the village from one comer D to construct a Health Centre. Join AC. Draw a line through D parallel to AC to meet BC produced in P. Then Itwaari must be given the land ECP adjoining his plot so as to form a triangular plot ABP as then
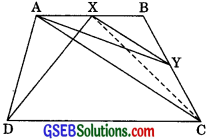
ar(ΔADE) = ar(ΔPEC)
Proof: ∴ ΔDAP and ΔDCP are on the same base DP and between the parallels DP and AC.
∴ ar(ΔDAP) = ar(ΔDCP) ………..(1)
∴ Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
⇒ ar(ΔDAP) – ar(ΔDEP) = (ΔDCP) – ar(ΔDEP)
Subtracting the same areas from both sides.
⇒ ar(ΔADE) = ar(ΔPCE)
⇒ ar(ΔADE) + ar(□ABCE) = ar(ΔPCE) + ar(□ABCE)
Adding the same areas to both sides.
⇒ ar(□ABCD) = ar(ΔABP)
Question 13.
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
[Hint: Join CX]
Solution:
Given: ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y.
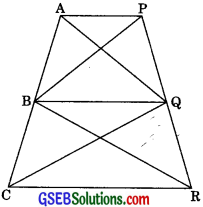
∴ ΔADX and ΔACX are on the same base AX and between the same parallels AB and DC.
∴ ar(ΔADX) = ar(ΔACX) …….(1)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area,
∴ ΔACX and ΔACY are on the same base AC and between the same parallels AC and XY.
∴ ar(ΔACX) = ar(ΔACY) …….(2)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
From (1) and (2), we get
ar(ΔADX) = ar(ΔACY)
![]()
Question 14.
In figure, AP || BQ || CR. Prove that ar(ΔAQC) = ar(ΔPBR).

Solution:
∴ ABAQ and ABPQ are on the same base BQ and between the same parallels BQ and AP.
∴ ar(ΔBAQ) = ar(ΔBPQ) ……..(1)
∴ Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Similarly, ΔBCQ and ΔBQR are on the same base BQ and between the same parallels BQ and CR.
∴ ar(ΔBCQ) = ar(ΔBQR) ……..(2)
Adding the corresponding sides of (1) and (2), we get
ar(ΔBAQ) + ar(ΔBCQ) = ar(ΔBPQ) + ar(ΔBQR)
∴ ar(ΔAQC) = ar(ΔPBR).
Question 15.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
Solution:
Given: ar(ΔAOD) = ar(ΔBOC)
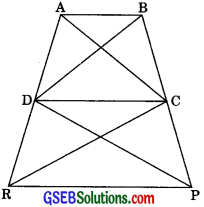
⇒ ar(ΔAOD) + ar(ΔAOB) = ar(ΔBOC) + ar(ΔAOB)
Adding the same areas on both sides.
⇒ ar(ΔABD) = ar(ΔABC)
But ΔABD and ΔABC are on the same base AB.
∴ ΔABD and ΔABC will have equal corresponding altitudes.
∴ ΔABD and ΔABC will lie between the same parallels.
∴ AB || DC
∴ □ABCD is a trapezium.
A quadrilateral is a trapezium if exactly one pair of opposite sides is parallel.
![]()
Question 16.
In figure, ar(ΔDRC) = ar(ΔDPC) and ar(ΔBDP) = ar(ΔARC). Show that both the quadrilateral ABCD and DCPR are trapeziums.
Solution:
Given: ar(ΔDRC) = ar(ΔDPC) ……..(1)
But ΔDRC and ΔDPC are on the same base DC.
ΔDRC and ΔDPC will have equal corresponding altitudes.
∴ ΔDRC and ΔDPC will lie between the same parallels.
∴ DC || RP
∴ □DCPR is a trapezium.
A quadrilateral is a trapezium if exactly one pair of opposite sides are parallel.
Again, ar(ΔBDP) = ar(ΔARC)
⇒ ar(ΔBDC) + ar(ΔDPC) = ar(ΔADC) + ar(ΔDRC)
⇒ ar(ΔBDC) = ar(ΔADC) [using (1)]
But ΔBDC and ΔADC are on the same base DC.
∴ ΔBDC and ΔADC will have equal corresponding altitudes.
∴ ΔBDC and ΔADC will lie between the same parallels.
∴ AB || DC
∴ □ABCD is a trapezium
A quadrilateral is a trapezium if exactly one pair of opposite sides is parallel.