GSEB Solutions Class 9 Science Chapter 9 બળ તથા ગતિના નિયમો

Gujarat Board GSEB Solutions Class 9 Science Chapter 9 બળ તથા ગતિના નિયમો Textbook Questions and Answers, Intext Questions, Textbook Activities Pdf.

બળ તથા ગતિના નિયમો Class 9 GSEB Solutions Science Chapter 9

GSEB Class 9 Science બળ તથા ગતિના નિયમો Textbook Questions and Answers

સ્વાધ્યાયના પ્રશ્નોત્તર

પ્રશ્ન 1.
કોઈ પદાર્થ શૂન્ય અસંતુલિત બાહ્ય બળ અનુભવે છે. શું તે પદાર્થ માટે અશૂન્ય વેગથી ગતિ કરવી શક્ય છે? જો હા, તો પદાર્થના વેગનું મૂલ્ય અને દિશા માટે જરૂરી શરતોનો ઉલ્લેખ કરો. 3 જો ના, તો કારણ સ્પષ્ટ કરો.
ઉત્તરઃ
હા,
જ્યારે કોઈ પદાર્થ પર લાગતું અસંતુલિત બાહ્ય બળ શૂન્ય હોય, તો ન્યૂટનના ગતિના બીજા નિયમ F = ma પરથી વ = 0 થાય.
(∵ અત્રે F = 0)

પદાર્થનો પ્રવેગ d = 0 હોય, તો તેનો વેગ = 0 હોય તેવું જરૂરી નથી. દા. ત., શરૂઆતથી જ પદાર્થ સુરેખ પથ પર ગતિમાં હોય અને તેના પર અસંતુલિત બાહ્ય બળ ન લાગે તો ન્યૂટનના ગતિના પ્રથમ નિયમ અનુસાર, તે પદાર્થ મૂળ દિશામાં જ અચળ ઝડપે ગતિ કરતો રહેશે. તેના વેગની દિશા અને વેગનું મૂલ્ય સમગ્ર ગતિ દરમિયાન અચળ જળવાઈ રહે છે.

ઉપરોક્ત હકીકત નીચેની શરતોને આધીન છે:

• પદાર્થ અચળ ઝડપે સુરેખ પથ પર ગતિ કરતો હોય.
• પદાર્થની ઝડપ બદલાતી હોય નહીં.
• પદાર્થની ગતિની દિશા બદલાવી ન જોઈએ.
• પદાર્થ જો કોઈ સપાટી પર ગતિ કરતો હોય, તો તેના ડે પર કોઈ ઘર્ષણબળ લાગવું જોઈએ નહીં.
• ગતિશીલ પદાર્થ પર હવાનું ઘર્ષણબળ પણ શૂન્ય હોવું જોઈએ.

પ્રશ્ન 2.
“જ્યારે કાર્પેટ(જાજમ)ને લાકડી વડે ફટકારવામાં આવે છે ત્યારે તેમાંથી ધૂળ બહાર આવે છે.” સમજાવો.
ઉત્તરઃ
કાર્પેટ (જાજમ) પ્રારંભમાં જ્યારે ટીંગાડેલી હોય કે લટકાવેલી હોય ત્યારે તેમાં ધૂળના રજકણો સ્થિર અવસ્થામાં હોય છે.
જ્યારે લાકડી વડે તેને ફટકારવામાં આવે ત્યારે જાજમ ગતિમાં આવે છે, પણ તેમાંના ધૂળના રજકણો પર કોઈ બાહ્ય બળ લાગતું ન હોવાથી તેઓ જડત્વના ગુણધર્મને લીધે સ્થિર અવસ્થામાં જ રહેવાનો પ્રયત્ન કરે છે. પરિણામે ધૂળના રજકણો જાજમમાંથી બહાર નીકળે છે અને જમીન પર પડે છે.

પ્રશ્ન 3.
બસની છત પર મૂકેલ સામાનને દોરડા વડે કેમ બાંધવામાં આવે છે?
ઉત્તર:
બસની છત (roof) પર મૂકેલ સામાનને દોરડા વડે બાંધવામાં ન આવે તો નીચેની ત્રણ પરિસ્થિતિઓમાં સામાન બસની છત પરથી નીચે પડી જાય:

1. જો સ્થિર બસ અચાનક ઝડપથી ગતિમાં આવે તો સામાન (સ્થિર સ્થિતિના) જડત્વના ગુણધર્મને લીધે તેની મૂળ અવસ્થામાં થતા ફેરફારનો વિરોધ કરશે અને સામાન પાછળની તરફ ધકેલાઈ જવાના કારણે નીચે પડી જશે.

2. જો બસ સુરેખ પથ પર અચળ વેગથી ગતિ કરતી હોય અને તેનો ડ્રાઇવર અચાનક બ્રેક લગાવે તો (ગતિના) જડત્વના ગુણધર્મને લીધે સામાન આગળની તરફ ધકેલાઈ જવાના કારણે નીચે પડી જશે.

3. જો બસ સુરેખ પથ પર ગતિ કરતી હોય અને તેનો ડ્રાઈવર વળાંક પાસે બસને ઝડપથી તીવ્ર વળાંક આપે તો (દિશાના) જડત્વના ગુણધર્મને લીધે સામાન મૂળ અવસ્થામાંથી સરકીને નીચે પડી જશે.
આમ, ઉપરની ત્રણેય પરિસ્થિતિઓની ચર્ચા પરથી સ્પષ્ટ છે કે, બસની છત પર મૂકેલ સામાનને દોરડા વડે બાંધવો જોઈએ.

પ્રશ્ન 4.
કોઈ બૅટ્સમૅન દ્વારા ક્રિકેટના બૉલને ફટકારાતાં તે જમીન પર ગબડે છે અને અમુક અંતર કાપીને સ્થિર થાય છે. દડો ધીમો પડીને અટકે છે. કારણ કે,
(a) બૅટ્સમૅન દ્વારા ક્રિકેટના બૉલને પૂરતા પ્રયત્નથી ફટકાર્યો નથી.
(b) વેગ બૉલ પર લગાડેલ બળના સમપ્રમાણમાં છે.
(c) બૉલની ગતિની વિરુદ્ધ દિશામાં એક બળ લાગી રહ્યું છે.
(d) બૉલ પર કોઈ અસંતુલિત બળ કાર્યરત નથી. તેથી બૉલ સ્થિર થવાનો પ્રયત્ન કરે છે. સાચો વિકલ્પ પસંદ કરો.
ઉત્તર:
(c) બૉલની ગતિની વિરુદ્ધ દિશામાં એક બળ લાગી રહ્યું છે.
બૉલની ગતિની વિરુદ્ધ દિશામાં તેના પર અવરોધક બળ લાગે છે, જે હવા સાથેના તેના ઘર્ષણને લીધે તથા જમીન સાથેના તેના ઘર્ષણને લીધે છે.

પ્રશ્ન 5.
સ્થિર અવસ્થામાં રહેલી એક ટ્રક કોઈ ટેકરી પરથી નીચે તરફ અચળ પ્રવેગથી ગતિની શરૂઆત કરે છે. તે 20 sમાં 400 m અંતર કાપે છે. તેનો પ્રવેગ શોધો. જો તેનું દળ 7 ટન હોય, તો તેના પર લાગતું બળ શોધો. (1 ટન = 1000 kg
ઉકેલઃ
અત્રે u = 0, s = 400 m, t = 20 s, a = ?, F = ?
s = ut + \(\frac{1}{2}\)at²
∴ 400 = 0 × 20 + \(\frac{1}{2}\)a × (20)²
∴ 400 = \(\frac{1}{2}\) × a × 400
∴ a = \(\frac{400 \times 2}{400}\)
∴ a = 2 m s^-2
હવે, દળ m = 7 મૅટ્રિક ટન = 7 × 1000 kg = 7000 kg
બળ F = ma
= 7000 × 2
= 14000 N
આમ, પ્રવેગ d = 2 m s^-2 અને બળ F = 14000 N

પ્રશ્ન 6.
1 kg દ્રવ્યમાન ધરાવતા એક પથ્થરને 20 m s^-1ના ૬ વેગથી તળાવની થીજી ગયેલ પાણીની સપાટી પર સપાટીને સમાંતર ફેંકવામાં આવે છે. પથ્થર 50 m અંતર કાપ્યા બાદ અટકી જાય છે. પથ્થર અને બરફ વચ્ચે લાગતું ઘર્ષણબળ કેટલું હશે?
ઉકેલઃ
અત્રે m = 1 kg, u = 20 m s^-1, s = 50 m, v = 0, F = ?
v² – u² = 2as
∴ (0)² – (20)² = 2a × 50 .
∴ – 400 = 100 a
∴ a = \(\frac{-400}{100}\)
= – 4 m s^-2
F = ma
= 1 × (- 4)
= – 4 N
ઋણ નિશાની સૂચવે છે કે, ઘર્ષણબળ પથ્થરની ગતિની વિરુદ્ધ દિશામાં લાગે છે અને તેની ગતિનો વિરોધ કરે છે.

પ્રશ્ન 7.
8000 kg દ્રવ્યમાન ધરાવતું રેલવે એન્જિન 2000 kg દ્રવ્યમાન ધરાવતા તેના પાંચ ડબ્બાઓને પાટા પર સમક્ષિતિજ દિશામાં ખેંચે છે. જો એન્જિન 40,000 N બળ લગાડતું હોય તથા પાટા દ્વારા 5000 N ઘર્ષણબળ લાગતું હોય, તો
(a) ચોખ્ખું પ્રવેગી બળ,
(b) ટ્રેનનો પ્રવેગ અને
(c) ડબ્બા 1 દ્વારા ડબ્બા 2 પર લાગતું બળ શોધો.
ઉકેલઃ
રેલવે એન્જિન અને પાંચ ડબ્બાઓનું કુલ દળ
M = (8000 + 5 × 20000) kg = 18000 kg
એન્જિન વડે લગાડાતું બળ F = 40000 N
પાટા દ્વારા લાગતું ઘર્ષણબળ f = 5000 N

(a) ચોખું પ્રવેગી બળ = F
= 40000 – 5000
= 35000 N

(b) F = ma પરથી,

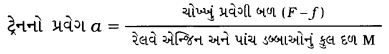
= \(\frac{35,000}{18,000}\)
= 1.944 m s^-2

(c) ડબ્બા 1 વડે ડબ્બા 2 પર લાગતું બળ એ ખરેખર ડબ્બા ૨ ક્રમાંક 2, 3, 4 અને 5 પર લાગતું હોય.
∴ ડબ્બા 1 દ્વારા ડબ્બા 2 પર લાગતું બળ
= (ડબ્બા ની પાછળ રહેલા ચાર ડબ્બાઓનું દળ) × (ટ્રેનનો પ્રવેગ)
= (4 × 2000) × 1.944
= 15552 N
આમ, (a) 35000 N (b) 1.944 ms (c) 15552 N

પ્રશ્ન 8.
એક ગાડીનું દળ 1500 kg છે. જો ગાડી 1.7 m sના પ્રતિપ્રવેગ(ઋણ પ્રવેગ)થી સ્થિર થતી હોય, તો ગાડી તથા રસ્તા વચ્ચે લાગતું બળ કેટલું હશે?
ઉકેલ:
અહીં m = 1500 kg, a = – 1.7 m s^-2, F = ?
F = ma
= 1500 × (- 1.7)
= – 2550 N
ઋણ નિશાની સૂચવે છે કે, ગાડી તથા રસ્તા વચ્ચે લાગતું બળ, ગાડીની ગતિની વિરુદ્ધ દિશામાં લાગે છે, એટલે કે ગાડીની ગતિનો વિરોધ કરે છે.

પ્રશ્ન 9.
કોઈ m દળનો પદાર્થ જેનો વેગ ઇ છે. તેનું વેગમાન કેટલું હશે?
(a) (mv)²
(b) mv²
(c) \(\frac{1}{2}\) mv²
(d) mv
સાચો વિકલ્પ પસંદ કરો. [1 ગુણ).
ઉકેલઃ
(d) mu, કારણ કે વેગમાન = દળ × વેગ

પ્રશ્ન 10.
જો આપણે લાકડાની એક પેટીને 200ષ જેટલું સમક્ષિતિજ બળ લગાડીને અચળ વેગથી લાદી પર ધકેલીએ તો પેટી પર લાગતું ઘર્ષણબળ કેટલું હશે?
ઉકેલ:
અત્રે, લાકડાની પેટી પર લગાડેલ બળ = F = 200 N
લાકડાની પેટી પર લાગતું ઘર્ષણબળ = f = ?
લાકડાની પેટી પર લાગતું ચોખ્ખું (net) બળ = F – f
હવે, લાકડાની પેટી આપેલ લાદી પર અચળ વેગથી ગતિ કરે છે. તેથી તેના પર લાગતું પરિણામી બળ = 0 (∵ ન્યૂટનનો ગતિનો પ્રથમ નિયમ)
અહીં, પરિણામી બળ = F – f છે.
∴ 0 = 200 – f થાય.
∴ f = 200 N

પ્રશ્ન 11.
1.5kg જેટલું સમાન દળ ધરાવતા બે પદાર્થો સુરેખ પથ પર એકબીજાની વિરુદ્ધ દિશામાં ગતિ કરી રહ્યા છે. અથડામણ પહેલાં બંનેનો વેગ 2.5 m s^-1 છે. જો અથડામણ બાદ બંને પદાર્થો એકબીજા સાથે જોડાઈ જતા હોય, તો તેમનો સંયુક્ત વેગ કેટલો હશે?
ઉકેલ:
અહીં, m₁ = m₂ = 1.5 kg
u₁ = 2.5 m s^-1, u₂ = – 2.5 m s^-1 (∵ તે વિરુદ્ધ દિશામાં ગતિ કરે છે.)
ધારો કે, અથડામણ બાદ સંયુક્ત પદાર્થનો વેગ D છે, તો વેગમાન સંરક્ષણના નિયમ પરથી,

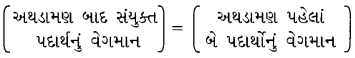
∴ (m₁ + m₂)v = m₁u₁ + m₂u₂
∴ (1.5 + 1.5) v = 1.5 × 2.5 + 1.5 × (- 2.5)
∴ 3v = 0
∴ v = 0 m s^-1
આમ, અથડામણ બાદ સંયુક્ત પદાર્થનો વેગ = 0 m s^-1

પ્રશ્ન 12.
ગતિના ત્રીજા નિયમ અનુસાર જ્યારે આપણે કોઈ પદાર્થને ૬ ધક્કો મારીએ ત્યારે તે પદાર્થ તેટલા જ બળથી આપણને વિરુદ્ધ દિશામાં ધક્કો મારતો હોય છે. જો આ પદાર્થ રસ્તાના છેડે ઊભેલ ટ્રક હોય, તો આપણા દ્વારા લગાડેલ બળથી તે ગતિમાં આવતી નથી. એક વિદ્યાર્થી આ ઘટનાને સમજાવતાં કહે છે કે, બે બળો સમાન અને પરસ્પર વિરુદ્ધ દિશામાં છે, જે એકબીજાની અસરો નાબૂદ કરે છે. આ તર્ક પર તમારાં સૂચન આપો અને બતાવો કે ટ્રક ગતિમાં કેમ નથી આવતી?
ઉત્તરઃ
વિદ્યાર્થીએ આપેલ તર્ક કે બે બળો સમાન અને પરસ્પર વિરુદ્ધ દિશામાં છે. તેથી એકબીજાની અસર નાબૂદ કરે છે અને રસ્તાના છેડે ઊભેલ ટ્રક ગતિમાં આવતી નથી, તે તદ્દન ખોટો છે. કારણ કે, ક્રિયાબળ અને પ્રતિક્રિયાબળ એક પદાર્થ પર લાગતાં બળો નથી. તે હંમેશાં જુદા જુદા પદાર્થો પર લાગતાં હોય છે. તેથી તેમની અસરો નાબૂદ થવાનો અહીં કોઈ પ્રશ્ન જ નથી.

હવે, રહી વાત ટ્રકની ગતિ કરવાની, તો ટ્રકનું દ્રવ્યમાન ખૂબ વધારે છે અને તેના પર આપણા દ્વારા લગાડેલ બળનું મૂલ્ય, ટ્રકના પૈડા અને રસ્તા વચ્ચે પ્રવર્તતા ઘર્ષણબળ કરતાં ઘણું નાનું છે. તેથી રસ્તાના છેડે ઊભેલ ટ્રક આપણે લગાડેલા બળને કારણે ગતિમાં આવતી નથી.

પ્રશ્ન 13.
10 m s^-1ના વેગથી ગતિ કરતા 200 g દળના હૉકીના બૉલને હૉકીસ્ટિક વડે ફટકારતાં તે મૂળ ગતિની વિરુદ્ધ દિશામાં 5 m s^-1ના વેગથી પાછો ફરે છે. આ ગતિ દરમિયાન હૉકીસ્ટિક વડે લાગતા બળથી હૉકીના બૉલના વેગમાનમાં થતો ફેરફાર ગણો.
ઉકેલ:
અહીં m = 200 g = 0.2 kg, બૉલનો પ્રારંભિક વેગ u = 10 m s^-1, બૉલનો અંતિમ વેગ v = – 5 m s’ (∵ હૉકીસ્ટિક વડે ફટકાર્યા બાદ હૉકીનો બૉલ મૂળ ગતિની વિરુદ્ધ દિશામાં ગતિ કરે છે.)
હૉકીના બૉલનું પ્રારંભિક વેગમાન = mu
= 0.2 × 10
= 2 kg m s^-1

હૉકીના બૉલનું અંતિમ વેગમાન = mv
= 0.2 × (5)
= -1 kg m s^-1

∴ હૉકીના બૉલના વેગમાનમાં થતો ફેરફાર
= (અંતિમ વેગમાન) – (પ્રારંભિક વેગમાન)
= (- 1 – 2)
= – 3 kg m s^-1

પ્રશ્ન 14.
10 g દળ ધરાવતી એક ગોળી સમક્ષિતિજ દિશામાં 150 m s^-1ના વેગથી ગતિ કરી લાકડાના એક બ્લૉક સાથે અથડાઈ, તેમાં ઘૂસીને 0.03 sમાં સ્થિર થાય છે. ગોળીએ બ્લૉકમાં ઘૂસ્યા બાદ કેટલું અંતર કાપ્યું હશે? લાકડાના બ્લૉક દ્વારા ગોળી પર લાગતા બળના મૂલ્યની પણ ગણતરી કરો.
ઉકેલઃ
અત્રે m = 10 g = 0.01 kg, ગોળીનો પ્રારંભિક વેગ u = 150 m s^-1, ગોળીનો અંતિમ વેગ v = 0, t = 0.03s
લાકડાના બ્લૉકમાં ઘૂસ્યા બાદ ગોળીએ કાપેલું અંતર s = ?
લાકડાના બ્લૉક વડે ગોળી પર લાગતાં બળનું મૂલ્ય |F| = ?
પ્રવેગ a = \(\frac{v-u}{t}\) = \(\frac{0-150}{0.03}\) = – 5000 m s^-2
અંતર = = ut + \(\frac{1}{2}\)at²
= 150 × 0.03 + \(\frac{1}{2}\) × (- 5000) × (0.03)²
= 4.5 – 2.25
= 2.25 m
ખળ F = ma
= 0.01 × (- 5000)
= – 50 N
∴ બળનું મૂલ્ય |F| = 50 N
આમ, લાકડાના બ્લૉકમાં ઘૂસ્યા બાદ ગોળીએ કાપેલું અંતર
s = 2.25 m
લાકડાના બ્લૉક વડે ગોળી પર લાગતાં બળનું મૂલ્ય |F| = 50 N

પ્રશ્ન 15.
1 kg દળ ધરાવતો પદાર્થ 10 m s^-1ના વેગથી સુરેખ પથ પર ગતિ કરી સ્થિર રહેલા 5kg દળના લાકડાના બ્લૉકને અથડાય છે. અથડામણ બાદ બંને સાથે સાથે તે જ દિશામાં ગતિ કરે છે, તો અથડામણ પહેલાં અને પછીનું કુલ વેગમાન ગણો તથા બંનેનો સંયુક્ત વેગ પણ ગણો.
ઉકેલ:
અહીં m₁ = 1 kg, u₁ = 10 m s^-1, m₂ = 5 kg, u₂ = 0
Just અથડામણ પહેલાં,
કુલ વેગમાન = m₁u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 kg m s^-1 ………… (1)
Just અથડામણ બાદ તંત્રનું એટલે કે (પદાર્થ + લાકડાના બ્લૉકનું) કુલ વેગમાન
= (m₁ + m₂) v જ્યાં, v = અથડામણ બાદ તંત્રનો સંયુક્ત વેગ
= (1 + 5) v
= 6 v ………… (2)

વેગમાન સંરક્ષણનો નિયમ વાપરતાં સમીકરણ (1) અને (2) પરથી,
6v = 10
∴ v = \(\frac{5}{3}\) m s^-1 …………. (3)
∴ Just અથડામણ બાદ તંત્રનું કુલ વેગમાન = 6v
= 6 × \(\frac{5}{3}\)
= 10 kg m s^-1

પ્રશ્ન 16.
અચળ પ્રવેગથી ગતિ કરતા 100 kg દળના એક પદાર્થનો વેગ 6sમાં 5ms^-1થી 8 m s^-1 થઈ જાય છે. પદાર્થના પ્રારંભિક અને અંતિમ વેગમાનોની ગણતરી કરો. પદાર્થ પર લાગતાં બળની પણ ગણતરી કરો.
ઉકેલ:
અહીં પદાર્થનું દળ m = 100 kg. પદાર્થનો પ્રારંભિક
વેગ u = 5 m s^-1 પદાર્થનો અંતિમ વેગ v = 8 m s^-1, t = 6s
પદાર્થનું પ્રારંભિક વેગમાન p₁ = mu
= 100 × 5 = 500 kgm ^-1
પદાર્થનું અંતિમ વેગમાન p₂ = mv
= 100 × 8 = 800 kg m s^-1
પદાર્થ પર લાગતું બળ F = ma
= m\(\left(\frac{v-u}{t}\right)\)
= 100\(\left(\frac{8-5}{6}\right)\)
= \(\frac{300}{6}\)
= 50 N
આમ, પદાર્થનું પ્રારંભિક વેગમાન = 500 kg m s^-1
પદાર્થનું અંતિમ વેગમાન = 800 kg m s^-1
પદાર્થ પર લાગતું બળ = 50 N

પ્રશ્ન 17.
અખ્તર, કિરણ અને રાહુલ કોઈ એક્સપ્રેસ હાઇવે પર તીવ્ર ; વેગથી ગતિ કરતી કારમાં બેઠેલા છે. અચાનક એક કીટક (insect) ગાડીની સામેના કાચ પર અથડાય છે અને ચોટી જાય છે. અખ્તર અને કિરણ આ સ્થિતિ પર વિચાર કરે છે. કિરણ એવું કહે છે કે, કીટકના વેગમાનમાં થતા ફેરફારનું મૂલ્ય કારના વેગમાનમાં થતા ફેરફારના મૂલ્યની સાપેક્ષમાં ખૂબ જ વધારે છે. (કારણ કે, કીટકના વેગમાં થતા ફેરફારનું મૂલ્ય કારના વેગમાં થતાં ફેરફારના મૂલ્ય કરતાં – ખૂબ જ વધારે છે.) અખ્તર એમ કહે છે કે, કારનો વેગ પ્રચંડ હોવાથી કાર દ્વારા કીટક પર ખૂબ જ મોટું બળ લાગે છે, જેના પરિણામે કીટક મૃત્યુ પામે છે. રાહુલે એક નવો વિચાર આપતાં કહ્યું કે કાર તથા કીટક બંને પર સમાન બળ લાગ્યું તથા તેમના વેગમાનમાં સમાન ફેરફાર થયો. – આ વિચારો પર તમારી પ્રતિક્રિયા જણાવો.
ઉત્તરઃ
1. કિરણનું સૂચન/પ્રસ્તાવ – કીટકના વેગમાનમાં થતા ફેરફારનું મૂલ્ય કારના વેગમાનમાં થતા ફેરફારના મૂલ્યની સાપેક્ષમાં ખૂબ જ વધારે છે.
તે તદન ખોટું છે.

2. અખ્તરનું સૂચન / પ્રસ્તાવ – કારનો વેગ પ્રચંડ હોવાથી કાર દ્વારા કીટક પર ખૂબ જ મોટું બળ લાગે છે.
તે તદ્દન ખોટું છે.

3. રાહુલનું સૂચન / પ્રસ્તાવ સાચો છે.
કારણ કે, બાહ્ય અસંતુલિત બળની ગેરહાજરીમાં વેગમાન સંરક્ષણના નિયમ પરથી, જ્યારે બે પદાર્થો અથડાય છે ત્યારે અથડામણ પહેલાંનું કુલ વેગમાન અને અથડામણ પછીનું કુલ વેગમાન સમાન હોય છે. (અર્થાત્ p₁ + p₂ = p₁‘ + p₂‘)

વધુમાં તેમના આનુષંગિક વેગમાનમાં થતા ફેરફાર સમાન મૂલ્યના હશે પણ નિશાની વિરુદ્ધ હશે. અર્થાતુ બંનેના વેગમાનમાં થતા ફેરફાર પરસ્પર વિરુદ્ધ દિશામાં હશે. (અર્થાત્ (p<sub2’ – p₁) = – (p₁‘ – p₁))

∴ આપેલ સમયગાળામાં કાર તથા કીટક બંને પર સમાન મૂલ્યનું બળ લાગ્યું હશે, કારણ કે ક્રિયાબળ અને પ્રતિક્રિયાબળ સમાન મૂલ્યના હોય છે. પણ કીટકનું દળ, કારના દળની સાપેક્ષમાં અવગણી શકાય તેટલું નાનું હોવાથી કીટકનાં વેગમાં થતો ફેરફાર ખૂબ વધારે હશે.

પ્રશ્ન 18.
10 kg SCUHIY Galad wis jala (dumb-bell) 80 cm ઊંચાઈએથી જમીન પર પડે તો તે જમીનને કેટલું વેગમાન આપશે? તેનો અધોદિશામાં પ્રવેગ 10 m sી લો.
ઉકેલઃ
અત્રે m = 10 kg, h = s = 80 cm = 0.8 m, a = 10 m s^-2, u = 0.
v² – u² = 2as
∴v² – (0)² = 2(10) × 0.8
∴ v² = 16
∴ v = 4 m s^-1
∴ ડંબેલ જમીન સાથે just અથડામણ કરે તે વખતે તેનું વેગમાન,
p = mv
= 10 × 4
= 40 kg m s^-1
∴ જમીનને તબદીલ (transfer) થયેલું વેગમાન = 40 kgm s^-1

GSEB Class 9 Science બળ તથા ગતિના નિયમો Intext Questions and Answers

Intext પ્રશ્નોતર [પાપુ. પાના નં.118]

પ્રશ્ન 1.
નીચેના પૈકી કોનું જડત્વ વધુ છેઃ
(a) રબરનો દડો અને તેટલા જ પરિમાણવાળો પથ્થર
(b) સાઈકલ અને ટ્રેન
(c) પાંચ રૂપિયાનો સિક્કો અને એક રૂપિયાનો સિક્કો.
ઉત્તર:
કોઈ પદાર્થનું દ્રવ્યમાન તેના જડત્વનું માપ છે. આપેલા જુદા જુદા પદાર્થોમાંથી જે પદાર્થનું દળ વધુ હોય તેનું જડત્વ વધારે હોય છે.
∴ (a) પથ્થર (b) ટ્રેન (c) પાંચ રૂપિયાનો સિક્કો.

પ્રશ્ન 2.
નીચે આપેલા ઉદાહરણમાં દડાનો વેગ કેટલી વાર બદલાય છે તે જાણવાનો પ્રયાસ કરોઃ
ફૂટબૉલનો એક ખેલાડી બૉલ પર કિક મારીને બૉલને પોતાની ટીમના બીજા ખેલાડી પાસે પહોંચાડે છે. બીજો ખેલાડી તે દડાને કિક મારીને ગોલ તરફ પહોંચાડવાનો પ્રયત્ન કરે છે. પ્રતિસ્પર્ધી ટીમનો ગોલકીપર દડાને પકડે છે અને પોતાની ટીમના ખેલાડી તરફ કિક મારે છે.” સાથે સાથે દરેક કિસ્સામાં બળ લગાડનાર કારક (Agent) પણ ઓળખી બતાવો.
ઉત્તરઃ
1. પહેલી વખત જ્યારે ફૂટબૉલનો એક ખેલાડી બૉલ પર કિક મારીને બૉલને પોતાની ટીમના બીજા ખેલાડી પાસે પહોંચાડે છે. અહીં, આ કિસ્સામાં બળ લગાડનાર કારક એ એક ખેલાડી છે.

2. બીજી વખત જ્યારે તે જ ટીમનો બીજો ખેલાડી તે દડાને કિક મારીને ગોલ તરફ પહોંચાડવાનો પ્રયત્ન કરે છે. અહીં, આ કિસ્સામાં બળ લગાડનાર કારક એ તે જ ટીમનો બીજો ખેલાડી છે.

3. ત્રીજી વખત પ્રતિસ્પર્ધી ટીમનો ગોલકીપર દડાને પકડે છે (દડાને રોકે છે). અહીં, આ કિસ્સામાં બળ લગાડનાર કારક એ પ્રતિસ્પર્ધી ટીમનો ગોલકીપર છે.

4. ચોથી વખત આ ગોલકીપર પોતાની ટીમના ખેલાડી તરફ કિક મારીને બૉલને પહોંચાડે છે.
અહીં, આ કિસ્સામાં બળ લગાડનાર કારક એ ગોલકીપર છે.
આમ, અત્રે આપેલા ઉદાહરણમાં દડાનો વેગ કુલ ચાર વખત બદલાય છે.

પ્રશ્ન 3.
“કોઈ ઝાડની ડાળીને તીવ્રતાથી હલાવતાં કેટલાંક પણે કેમ ડાળીમાંથી છૂટી (નીચે પડી) જાય છે?” સમજાવો.
ઉત્તર:
ઝાડની ડાળીને તીવ્રતાથી હલાવતાં પહેલાં તેનાં પર્ણો સ્થિર અવસ્થામાં હોય છે.
હવે, ઝાડની ડાળીને પકડીને તીવ્રતાથી હલાવતાં ડાળીઓ ગતિમાં આવે છે પણ તેનાં પણ જડત્વના ગુણધર્મને લીધે પોતાની મૂળ સ્થિર અવસ્થામાં રહેવાનો પ્રયત્ન કરે છે, તેથી તેનાં કેટલાંક પણ તૂટીને નીચે પડે છે.

(અહીં, ઝાડની ડાળીને પકડીને તેના પર તીવ્રતાથી બળ લગાડવામાં છે આવે છે તેથી લગાડેલ બળને પણ સુધી પહોંચવા માટે ખૂબ નાનો સમયગાળો મળે છે. જો ઝાડની ડાળીને ધીરે ધીરે હલાવવામાં આવે, તો ડાળી પર લગાડેલ બળને તેનાં પણ સુધી પહોંચવા માટે પૂરતો છે સમય મળી રહે છે, પરિણામે પણ તૂટીને નીચે પડી જતા નથી.)

પ્રશ્ન 4.
જ્યારે કોઈ ગતિશીલ બસ અચાનક અટકી જાય તો તમે આગળ તરફ નમી પડો છો અને ઊભી રહેલી બસ અચાનક ગતિમાન (ચાલુ) થાય તો પાછળ તરફ નમી પડો છો. કેમ?
ઉત્તર:
જ્યારે બસ ગતિમાં હોય છે ત્યારે તેની અંદર ઊભેલા આપણે પણ બસની ગતિની દિશામાં ગતિમાં હોઈએ છીએ. પણ જ્યારે બસ પર બ્રેક લગાડીને અચાનક તેને સ્થિર કરવામાં આવે છે, ત્યારે બસની સંપર્કમાં રહેલા આપણા પગ અને શરીરનો નીચેનો ભાગ તરત જ સ્થિર થઈ જાય છે, પરંતુ શરીરનો ઉપરનો ભાગ ગતિના જડત્વને કારણે ગતિમાં રહેવાનો પ્રયત્ન કરે છે, તેથી આપણે આગળ તરફ નમી પડીએ છીએ.

જ્યારે બસ ઊભી રહેલી હોય ત્યારે તેની અંદર ઊભેલા આપણે પણ સ્થિર અવસ્થામાં હોઈએ છીએ. પણ જ્યારે બસ અચાનક ચાલુ થાય અને પ્રવેગિત થાય ત્યારે બસની સંપર્કમાં રહેલા આપણા પગ અને શરીરનો નીચેનો ભાગ તરત જ ગતિમાં આવે છે.

પરંતુ શરીરનો ઉપરનો ભાગ જડત્વના ગુણધર્મને લીધે સ્થિર અવસ્થામાં રહેવાનો પ્રયત્ન કરે છે, તેથી આપણે પાછળ તરફ નમી પડીએ છીએ.

Intext પ્રશ્નોત્તર [પા.પુ. પાના નં. 126-127]

પ્રશ્ન 1.
જો ક્રિયાબળ અને પ્રતિક્રિયાબળ હંમેશાં સમાન હોય, તો સમજાવો કે ઘોડો ગાડીને કેવી રીતે ખેંચી શકે છે?
ઉત્તર:
ઘોડાગાડી તંત્રના ગતિના કિસ્સામાં ખરેખર બળોની ત્રણ જોડ અસ્તિત્વમાં હોય છે?

• ઘોડા વડે ગાડી પર અને ગાડી વડે ઘોડા પર લાગતાં બળોની જોડ.
• ઘોડા વડે જમીન પર અને જમીન વડે ઘોડા પર લાગતાં બળોની જોડ.
• ગાડી વડે જમીન પર અને જમીન વડે ગાડી પર લાગતાં બળોની જોડ.

અહીં, ઘોડાનું અને ગાડીનું વજન (બળ) ધ્યાનમાં લીધું નથી, કારણ કે સમક્ષિતિજ દિશામાંની ગતિ માટે સમક્ષિતિજ દિશામાં તેમની કોઈ અસરકારકતા નથી.
ઘોડાગાડીની ગતિના ચોક્કસ વર્ણન માટે ઉપરની ત્રણ બળોની જોડ (કુલ બળોની સંખ્યા 6) ધ્યાનમાં લેવામાં આવે છે.

પ્રારંભમાં ઘોડો, ગાડી પર કંઈક મૂલ્યનું બળ લગાડે છે ત્યારે ન્યૂટનના ગતિના ત્રીજા નિયમ અનુસાર ગાડી પણ ઘોડા પર તેટલા જ મૂલ્યનું બળ વિરુદ્ધ દિશામાં લગાડે છે. પ્રથમ દષ્ટિએ જોતાં ક્રિયાબળ અને પ્રતિક્રિયાબળ સમાન મૂલ્યના અને પરસ્પર વિરુદ્ધ દિશામાં હોવાથી, એકબીજાની અસર નાબૂદ કરે છે અને ગાડી ગતિ કરી શકતી નથી.

પણ જો ઘોડો પોતાના પગ વડે જમીન પર પૂરતું બળ લગાડશે, જે ઘોડા પર પાછળની દિશામાં લાગતા પરિણામી (કુલ) બળ કરતાં વધુ હશે તો ઘોડાગાડી ગતિ કરવા લાગશે.
તેમ કરવા માટે ઘોડો થોડોક આગળ-નીચે તરફ વળીને પગ વડે જમીન પર (પાછળની દિશામાં) પૂરતાં મૂલ્યનું બળ લગાડે છે (એટલે કે જમીનને દબાવે છે, ત્યારે જમીન પણ ઘોડા પર તેટલા જ મૂલ્યનું પ્રતિક્રિયાબળ વિરુદ્ધ દિશામાં લગાડે છે.

પરિણામે, હવે ગાડી પર આગળની દિશામાં લાગતું પરિણામી બળ, ઘોડા પર પાછળની દિશામાં લાગતાં પરિણામી બળ કરતાં વધી જાય છે અને ઘોડાગાડી આગળ તરફ ચાલવા માંડે છે (પ્રવેગિત ગતિ કરવા લાગે છે.)

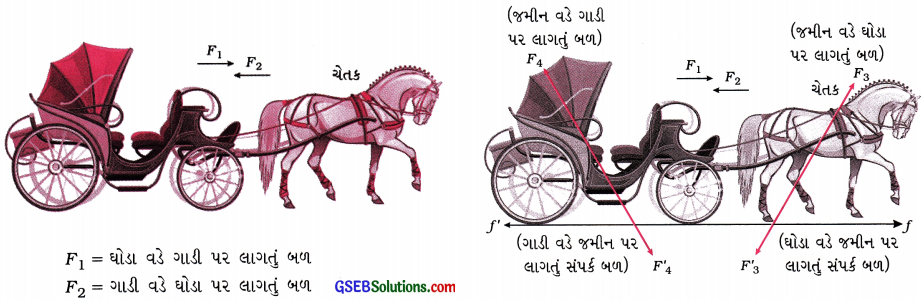
[આકૃતિ 9.18]
નોંધઃ આકૃતિ 9.18 પરીક્ષામાં દોરવાની નથી

પ્રશ્ન 2.
એક ફાયરબ્રિગેડના કર્મચારીને તીવ્ર વેગથી મોટી ? માત્રામાં પાણી બહાર ફેંકતી નળીને પકડવામાં તકલીફ કેમ પડે છે? સમજાવો.
ઉત્તર:
જ્યારે વાળી કે વળી શકે તેવી નળી (hose) વડે ફાયરબ્રિગેડનો કર્મચારી પાણીનો છંટકાવ તીવ્ર વેગથી મોટી માત્રામાં આગળની તરફ કરે છે, ત્યારે પાણીની ધારા પ્રચંડ વેગમાનથી બહાર તરફ નીકળે છે.

પરિણામે, નળીને પાછળની દિશામાં તેટલું જ વેગમાન તેટલા સમયમાં મળે છે અર્થાત્ નળી પર (અને ફાયરબ્રિગેડ કર્મચારી પર) પાછળની દિશામાં મોટા મૂલ્યનું પ્રત્યાઘાતી બળ લાગે છે. તેથી ઘણી વાર ફાયરબ્રિગેડ કર્મચારીના હાથમાંથી નળી સરકી જઈ શકે છે. તેથી ફાયરબ્રિગેડના કર્મચારીને આ નળી પકડી રાખવામાં ખૂબ મુશ્કેલી તકલીફનો સામનો કરવો પડે છે.

પ્રશ્ન 3.
એક 50 g દ્રવ્યમાનની ગોળી 4kg દ્રવ્યમાનની રાઇફલમાંથી 35 m s^-1 વેગથી છોડવામાં આવે છે. રાઇફલનો પ્રારંભિક રિકૉઇલ વેગ ગણો.
ઉકેલ:
રાઇફલનું દળ m₁ = 4 kg
ગોળીનું દળ m₂ = 50 g = 0.05 kg
રાઇફલનો પ્રારંભિક વેગ u₁ = 0 m s^-1
ગોળીનો પ્રારંભિક વેગ u₂ = 0 m s^-1
ગોળીનો અંતિમ વેગ v₂ = 35 m s^-1
રાઇફલનો અંતિમ વેગ v₁ = ?
વેગમાનના સંરક્ષણનો નિયમ વાપરતાં,
m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂
∴ 4 × v₁ + 0.05 × 36 = 4 × 0 + 0.05 × 0
∴ 4v₁ = – 0.05 × 35
∴v₁ = \(\frac{0.05 \times 35}{4}\)
= – \(\frac{1.75}{4}\)
= – 0.4375 m s^-1
≈ – 0.44 m s^-1
ઋણ નિશાની સૂચવે છે કે રાઇફલ, ગોળીની ગતિની વિરુદ્ધ દિશામાં (પાછળની તરફ) ગતિ કરે છે.
રાઇફલનો પ્રારંભિક રિકૉઇલ વેગ = 0.44 m s^-1

પ્રશ્ન 4.
100 g અને 200 g દળના બે પદાર્થો એક જ રેખા પર એક જ દિશામાં અનુક્રમે 2 m s^-1 તથા 1 m s^-1ના વેગથી ગતિ કરે છે.
બંને પદાર્થો અથડાય છે અને અથડામણ બાદ પ્રથમ પદાર્થનો વેગ 1.67 m s^-1 થતો હોય, તો બીજા પદાર્થનો વેગ નક્કી કરો.
ઉકેલ:
પ્રથમ પદાર્થનું દળ m₁ = 100 g = 0.1 kg
બીજા પદાર્થનું દળ m₂ = 200 g = 0.2 kg
પ્રથમ પદાર્થનો પ્રારંભિક વેગ u₁ = 2 m s^-1
બીજા પદાર્થનો પ્રારંભિક વેગ u₂ = 1 m s^-1
પ્રથમ પદાર્થનો અંતિમ વેગ v₁ = 1.67 m s^-1
બીજા પદાર્થનો અંતિમ વેગ v₂ = ?
વેગમાનના સંરક્ષણનો નિયમ વાપરતાં,
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
∴ 0.1 × 2 + 0.2 × 1 = 0.1 × 1.67 + 0.2 × v₂
∴ 0.2 + 0.2 = 0.167 + 0.209
∴ 0.4 – 0.167 = 0.2n₂
∴ 0.2v₂ = 0.233
∴ v₂ = \(\frac{0.233}{0.2}\)
= 1.165 m s^-1
બીજા પદાર્થનો અંતિમ વેગ 1.165 m s^-1 છે.

GSEB Class 9 Science બળ તથા ગતિના નિયમો Textbook Activities

પ્રવૃત્તિ 9.1 [પા.પુ. પાના નં. 117]

• આકૃતિ 9.8માં દર્શાવ્યા અનુસાર કેરમની એકસરખી કૂકરીઓ (Coins)ને એક ઉપર એક એમ ગોઠવી થપ્પી (Pile) બનાવો.
• અન્ય એક કૂકરી અથવા સ્ટ્રાઇકરને પોતાની આંગળીઓની મદદથી સમક્ષિતિજ દિશામાં ફટકારી થપ્પીની સૌથી નીચેની કૂકરી જોડે પૂરતી તીવ્રતાથી અથડાવો.
• તમારું અવલોકન અને નિષ્કર્ષ જણાવો.

[આકૃતિ 9.8: સ્ટ્રાઇકરને તીવ્ર વેગથી કૂકરીની થપ્પી સાથે અથડાવતા ફક્ત સૌથી નીચેની કૂકરી થપ્પીમાંથી બહાર નીકળી જાય છે.]

અવલોકન: અત્રે સૌથી નીચેની કૂકરી પર પૂરતા બળથી સ્ટ્રાઇકર અફળાવવામાં આવે, તો માત્ર તેના સ્થિર અવસ્થામાં રહેવાના જડત્વના ગુણધર્મમાં ફેરફાર થાય છે. તેથી તે થપ્પીમાંથી (ઢગલીમાંથી) બહાર આવી જાય છે. પણ થપ્પીની બાકીની કૂકરીઓ પોતાના જડત્વના (સ્થિર સ્થિતિમાં રહેવાના) ગુણધર્મને લીધે થપ્પીમાં અકબંધ જળવાઈ રહીને અધોદિશામાં આવી જાય છે.

(અહીં નીચેની કૂકરી પર લગાડેલ બળને તેની ઉપરની કૂકરીઓ છે સુધી પહોંચવા માટેનો સમયગાળો ખૂબ નાનો મળે છે, નહીં તો ઉત્પન્ન કરેલી દખલ ઉપરની કૂકરીઓ સુધી પહોંચી જાય અને પછી હું બધી કૂકરીઓ અસ્તવ્યસ્ત રીતે વેરવિખેર થઈ જાય.)

નિષ્કર્ષ : કોઈ પણ પદાર્થ પોતાના જડત્વના ગુણધર્મને લીધે સ્થિર અવસ્થામાં જ રહેવાનો પ્રયત્ન કરે છે કે જ્યાં સુધી તેના પર અસંતુલિત બાહ્ય બળ ન લાગે.

પ્રવૃત્તિ 9.2 [પા.પુ. પાના નં. 118]

• આકૃતિ 9.9માં દર્શાવ્યા પ્રમાણે કાચના એક ખાલી ગ્લાસ પર કડક પત્તાને મૂકી તેની પર એક પાંચ રૂપિયાનો સિક્કો મૂકો.
• પત્તાને આંગળી વડે સમક્ષિતિજ દિશામાં (ખૂબ) ઝડપથી ધક્કો મારો.
• તમારું અવલોકન અને નિષ્કર્ષ જણાવો.

[આકૃતિ 9.9: આંગળીથી કડક પત્તાને (ખૂબ ઝડપે) ધક્કો મારતાં પત્તાની ઉપર રાખેલ સિક્કો નીચે રાખેલ ગ્લાસ(પ્યાલા)માં પડે છે.]

અવલોકન: અહીં કડક પત્તા પર બાહ્ય બળ લગાડતાં (કડક પત્તા પર સમક્ષિતિજ દિશામાં ધક્કો મારતાં અથવા તેને ઝડપથી ખેંચતા), માત્ર તેના સ્થિર અવસ્થામાં રહેવાના જડત્વના ગુણધર્મમાં ફેરફાર થાય છે તેથી તે બહાર તરફ ફેંકાઈ જાય છે. પણ તેના ઉપરનો સિક્કો પોતાના જડત્વના (સ્થિર અવસ્થામાં રહેવાના) ગુણધર્મને લીધે સ્થિર અવસ્થામાં રહેવાનો પ્રયત્ન કરે છે, પણ હવે સિક્કાને કડક પત્તાનો આધાર ન મળવાથી તે પ્યાલામાં પડી જાય છે. ”

(અત્રે કડક પત્તા પર લગાડેલ બળને (અથવા ઉત્પન્ન કરેલ દખલને) તેની ઉપરના સિક્કા સુધી પહોંચવા માટે સમયગાળો ખૂબ નાનો મળે છે.)

નિષ્કર્ષ: કોઈ પણ પદાર્થ પોતાના જડત્વના ગુણધર્મને લીધે સ્થિર અવસ્થામાં જ રહેવાનો પ્રયત્ન કરે છે કે જ્યાં સુધી તેના પર અસંતુલિત બાહ્ય બળ ન લાગે.

પ્રવૃત્તિ 9.8 [પા.પુ. પાના નં. 118]

• પાણી ભરેલ ગ્લાસ (પ્યાલો) કોઈ ટ્રે પર મૂકો.
• ટ્રેને હાથથી પકડી જેટલું થઈ શકે તેટલા જોરથી ગોળ ફરો.
• આપણે જોઈએ છીએ કે પાણી છલકાય છે. કેમ?

અવલોકન: જ્યારે આપણે ટ્રેને બને એટલી ઝડપે ગોળ ફેરવીએ છીએ, ત્યારે આપણે ટ્રે પર લગાડેલા બળને ગ્લાસમાં રહેલા પાણી સુધી પહોંચવા માટે ખૂબ નાનો સમયગાળો મળે છે. તેથી ગ્લાસમાંનું પાણી પોતાના જડત્વના (સ્થિર અવસ્થામાં રહેવાના) ગુણધર્મને લીધે છલકાઈ જાય છે.

(જો આપણે ટ્રેને ખૂબ ધીમેથી ગોળ ફેરવીશું તો ટ્રે પર લગાડેલ બળને ગ્લાસમાંના પાણી સુધી પહોંચવા માટે પૂરતો સમય મળી રહેશે અને પરિણામે ગ્લાસમાંનું પાણી છલકાશે નહીં.)

નિષ્કર્ષ: કોઈ પણ પદાર્થ પોતાના જડત્વના ગુણધર્મના લીધે સ્થિર અવસ્થામાં જ રહેવાનો પ્રયત્ન કરે છે કે જ્યાં સુધી તેના પર અસંતુલિત બાહ્ય બળ ન લાગે.
પણ, અહીં પદાર્થ પર જ્યારે અસંતુલિત બાહ્ય બળ લાગે છે ત્યારે પદાર્થનો સ્થિર રહેવાનો જડત્વનો ગુણધર્મ નાશ પામે છે.

પ્રવૃત્તિ 9.4 [પા.પુ. પાના નં 123]

• બે બાળકોને ગરગડીવાળા પાટિયા (Cart) પર આકૃતિ 9.14માં દર્શાવ્યા પ્રમાણે ઊભા રહેવાનું કહો.
• તેમને રેતીથી ભરેલો થેલો કે બીજો કોઈ ભારે પદાર્થ આપો. હવે તેમને આ થેલાને કૅચ કરવાની રમત રમવાનું કહો.
• શું રેતીનો થેલો ફેંકવાને કારણે (ક્રિયાબળ) તે બંને તત્કાળ પ્રતિક્રિયાબળનો અનુભવ કરશે?
• તમે પાટિયાની ગરગડી પર એક સફેદ રેખા દોરો કે જેથી જ્યારે બંને બાળકો થેલાને ફેંકે ત્યારે બંને પાટિયાની ગતિનું અવલોકન કરી શકાય.
• હવે બંને બાળકોને કોઈ એક પાટિયા પર ઊભા રાખો તથા બીજા એક બાળકને બીજા પાટિયા પર ઊભો રાખો.

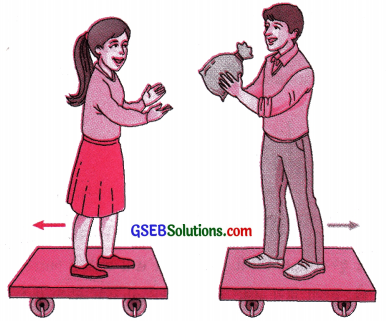
[આકૃતિ 9.14].

[આ પ્રવૃત્તિમાં દર્શાવેલ પાટિયું 50 cm × 100 cm આકારના 12 mm કે 18mm જાડાઈના પ્લાયવુડ બોર્ડ અને બે જોડ બૉલબેરિંગ વ્હીલ દ્વારા બનાવી શકાય છે. (સ્કેટ વ્હીલનો ઉપયોગ વધારે સારો પડશે.) સ્કેટ બોર્ડ અહીં એટલું અસરકારક નહિ રહે કારણ કે, તેના દ્વારા સુરેખ પથ ગતિ કરવી મુશ્કેલ છે.].

અવલોકન: જ્યારે બંને બાળકો જુદા જુદા ગરગડીવાળા પાટિયા પર ઊભા રહીને રેતી ભરેલો થેલો એકબીજા તરફ ફેંકવાની રમત રમે છે, ત્યારે બંને ગરગડીવાળા પાટિયા પર બહારની તરફ તત્કાળ પ્રતિક્રિયાબળ લાગે છે.

પરિણામે જ્યારે છોકરો, છોકરી તરફ રેતી ભરેલો થેલો ફેંકે છે કે તરત જ તે ક્ષણે છોકરાવાળું ગરગડીવાળું પાટિયું બહાર તરફ ગતિ કરવા લાગે છે. તે જ પ્રમાણે જ્યારે છોકરી, છોકરા તરફ રેતી ભરેલો થેલો ફેંકે છે કે તરત જ તે ક્ષણે છોકરીવાળું ગરગડીવાળું પાટિયું બહાર તરફ ગતિ કરવા લાગે છે. જે બંને ગરગડીવાળા પાટિયા પર તીર દોરીને દર્શાવેલ છે.

હવે, ક્રિયાબળ અને પ્રતિક્રિયાબળ સમાન મૂલ્યના (અને પરસ્પર વિરુદ્ધ દિશામાં) હોય છે. પણ સામાન્ય રીતે છોકરીનું દળ, છોકરાના દળ કરતાં ઓછું હોય છે તેથી વ = F/m પરથી છોકરીવાળા ગરગડીવાળા પાટિયાનો પ્રવેગ, છોકરાવાળા ગરગડીવાળા પાટિયા કરતાં વધુ હોય છે. તેથી આપેલા સમયગાળામાં છોકરીવાળું ગરગડીવાળું પાટિયું, છોકરાવાળા ગરગડીવાળા પાટિયા કરતાં વધુ અંતર કાપે છે જે બંને પાટિયાની ગરગડી પર દોરેલ સફેદ રેખા વડે જાણી શકાય છે.

જો એક ગરગડીવાળા પાટિયા પર બે બાળકો ઊભા હોય અને બીજા ગરગડીવાળા પાટિયા પર એક બાળક ઊભો હોય અને ઉપરની પ્રવૃત્તિનું પુનરાવર્તન કરવામાં આવે, તો બંને ગરગડીવાળા પાટિયા પર બહારની તરફ તત્કાળ પ્રતિક્રિયાબળ લાગે છે. પણ ન્યૂટનના ગતિના બીજા નિયમ a = F/m પરથી, બંને ગરગડીવાળા પાટિયા પર એકસરખાં મૂલ્યના બળો લાગવા છતાં તેમનામાં ઉદ્ભવતા પ્રવેગનાં મૂલ્યો જુદાં જુદાં હોય છે. કારણ કે બંને તંત્ર (system) (છોકરા + ગરગડીવાળું પાટિયું)ના દ્રવ્યમાન જુદા જુદા છે. પરિણામે આપેલા સમયગાળામાં તેમના દ્વારા બહારની તરફ કાપેલાં અંતરો જુદાં જુદાં હોય છે, જે બંને પાટિયાની ગરગડી પર દોરેલ સફેદ રેખા વડે જાણી શકાય છે.

નિષ્કર્ષ: ક્રિયાબળ અને પ્રતિક્રિયાબળનાં મૂલ્યો સમાન અને દિશા પરસ્પર વિરુદ્ધ હોય છે. તેઓ જુદા જુદા પદાર્થો પર લાગે છે અને જુદાં જુદાં મૂલ્યોના પ્રવેગ તેમનામાં ઉત્પન્ન કરે છે, જો બંને પદાર્થોનાં દળ જુદાં જુદાં હોય.

પ્રવૃત્તિ 9.5 [પા.પુ. પાના નં 124].

• એક મોટો ફુગ્ગો લો તથા તેને પૂરેપૂરો ફુલાવો. તેના મુખને દોરી વડે બાંધી દો. સેલોટેપની મદદથી એક સ્ટ્રૉને ફુગ્ગા પર ચીપકાવો.
• સ્ટ્રૉમાંથી એક દોરી પસાર કરો અને તેનો છેડો તમારા હાથમાં પકડો અથવા દીવાલ સાથે બાંધી દો.
• તમારા મિત્રને દોરીનો બીજો છેડો પકડવાનું કહો અથવા તેને દીવાલ પર અમુક અંતરે બાંધી દો. આ ગોઠવણ આકૃતિ 9.16માં દર્શાવેલ છે.
• હવે ફુગ્ગાના મુખ પર બાંધેલ દોરી છોડી દો અને હવાને ફુગ્ગાના મુખમાંથી બહાર નીકળવા દો.
• સ્ટ્રૉ સાથેના ફુગ્ગાની ગતિની દિશાનું અવલોકન કરો.

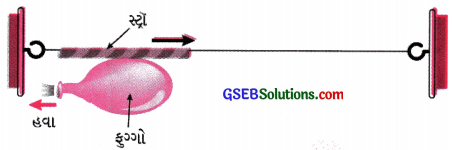
[આકૃતિ 9.16].

અવલોકન: જ્યારે ફુગ્ગાના મુખ આગળની દોરી છોડવામાં આવે છે, ત્યારે ફુગ્ગાના મુખમાંથી તેમાં ભરેલી હવા ઝડપથી બહારની તરફ નીકળે છે. ફુગ્ગા દ્વારા હવા પર બળ લાગતા હવા ફુગ્ગાની બહારની તરફની દિશામાં (જમણી બાજુથી ડાબી બાજુની દિશામાં) ગતિ કરે છે. આ બળને ક્રિયાબળ ગણી શકાય.

હવે આ બહાર નીકળેલી હવા દ્વારા ફુગ્ગા પર વિરુદ્ધ દિશામાં બળ લાગે છે. આથી ફુગ્ગો ડાબી બાજુથી જમણી બાજુની દિશા તરફ ગતિ કરે છે. જેને પ્રતિક્રિયાબળ ગણી શકાય. અહીં બંને બળો પરસ્પર વિરુદ્ધ દિશામાં છે. આ પરથી ન્યૂટનનો ગતિનો ત્રીજો નિયમ સમજી શકાય છે.

આ પ્રવૃત્તિની સમજૂતી વેગમાન સંરક્ષણના નિયમ પરથી નીચે મુજબ આપી શકાય:
પ્રારંભમાં સ્ટ્રૉ અને હવા ભરેલો મોટો ફુગ્ગો સ્થિર અવસ્થામાં છે. તેથી તંત્ર(સ્ટ્રૉ + હવા ભરેલા મોટા ફુગ્ગા)નું પ્રારંભિક કુલ વેગમાન શૂન્ય છે.

પણ જ્યારે ફુગ્ગાના મુખ પર બાંધેલ દોરી છોડવામાં આવે છે ત્યારે બાહ્ય અસંતુલિત બળની ગેરહાજરીમાં તેમાંથી હવા ઝડપથી ડાબી બાજુ ગતિ કરે છે. તેથી હવાને ડાબી બાજુ વેગમાન મળે છે. હવે તેટલું જ વેગમાન જો ફુગ્ગાને જમણી બાજુ મળે તો જ અંતિમ કુલવેગમાન શૂન્ય થાય અને વેગમાન સંરક્ષણનો નિયમ પળાય.

નિષ્કર્ષ: ક્રિયાબળ અને પ્રતિક્રિયાબળ સમાન મૂલ્યના અને પરસ્પર ‘ વિરુદ્ધ દિશામાં હોય છે અને અસંતુલિત બાહ્ય બળની ગેરહાજરીમાં તંત્રનું કુલ વેગમાન અચળ જળવાઈ રહે છે.

પ્રવૃત્તિ 9.6 [પા.પુ. પાના નં. 124]

• સારી ગુણવત્તા ધરાવતા કાચની બનેલી એક કસનળી (ટેસ્ટટ્યૂબ) લો અને તેમાં થોડું પાણી ઉમેરો. કસનળીના મુખ પર એક બૂચ લગાવો.
• આકૃતિ 9.17 (a)માં દર્શાવ્યા પ્રમાણે કસનળીને બે દોરીઓની મદદથી સમક્ષિતિજ દિશામાં લટકાવો.
• બર્નરની મદદથી કસનળીને ત્યાં સુધી ગરમ કરો જ્યાં સુધી પાણીનું છે સંપૂર્ણ બાષ્પીભવન ન થાય અને બૂચ બહાર નીકળી ન જાય.
• બૂચ અને કસનળીના વેગના ફેરફારનું પણ અવલોકન કરો.

અવલોકન: બૂચ પર ગરમ વરાળ દ્વારા ક્રિયાબળ લાગવાને લીધે તે જમણી બાજુ તરફ ધકેલાય છે. તે જ ક્ષણે કસનળી પર પ્રતિક્રિયાબળ લાગવાને લીધે તે ડાબી બાજુ તરફ ધકેલાય છે. (ક્રિયાબળ અને પ્રતિક્રિયાબળનાં મૂલ્યો સમાન છે અને બંને આંતરિક બળો છે.)

હવે, બૂચનું દળ કસનળીનાં દળ કરતાં ઓછું હોવાના કારણે ન્યૂટનના ગતિના બીજા નિયમ a = \(\frac{F}{m}\) પરથી આપેલ સમયમાં બૂચમાં ઉદ્ભવેલો પ્રવેગ, કસનળીમાં ઉદ્ભવેલ પ્રવેગ કરતાં વધુ છે. તેથી બૂચનો વેગ કસનળીના વેગ કરતાં વધુ હોય છે.

ઉપરોક્ત અવલોકન રેખીય વેગમાન સંરક્ષણના નિયમના સંદર્ભમાં નીચે મુજબ સમજાવી શકાયઃ
પ્રારંભમાં બૂચ અને થોડું પાણી ભરેલી કસનળી બંને સ્થિર અવસ્થામાં છે. તેથી તેમનું પ્રારંભિક કુલ વેગમાન શૂન્ય છે.

જ્યારે બૂચ જમણી બાજુ તરફ ધકેલાય છે ત્યારે કોઈ પણ પ્રકારનું બાહ્ય અસંતુલિત બળ હાજર નથી. તેથી બૂચ અને કસનળીનું કુલ (અંતિમ) વેગમાન પણ શૂન્ય રહે. માટે કસનળીનું વેગમાન અને બૂચનું વેગમાન એકસમાન મૂલ્યના અને પરસ્પર વિરુદ્ધ દિશામાં હશે.

હવે વેગમાન = દળ × વેગ હોવાથી અને કસનળીનું દળ, બૂચના દળ કરતાં વધુ હોવાથી કસનળીનો વેગ બૂચના વેગ કરતાં ઓછો છે. હું તેથી આપેલ સમયગાળામાં કસનળીએ કાપેલું અંતર, બૂચ કરતાં ઓછું છે.

નિષ્કર્ષ: ક્રિયાબળ અને પ્રતિક્રિયાબળ સમાન મૂલ્યના અને પરસ્પર છે વિરુદ્ધ દિશામાં છે. વધુમાં બાહ્ય અસંતુલિત બળની ગેરહાજરીમાં તંત્રના (અર્થાત્ થોડું પાણી ભરેલી કસનળી + બૂચનાં) વેગમાનનું સંરક્ષણ થાય છે.

વધારાનો સ્વાધ્યાય (Additional Exercises)

પ્રશ્ન 1.
નીચેના કોષ્ટકમાં એક પદાર્થની ગતિ માટે સમય અને અંતરનાં મૂલ્યો દર્શાવ્યાં છેઃ

સમય સેકન્ડમાં	અંતર મીટરમાં
0	0
1	1
2	18
3	27
4	64
5	125
6	216
7	343

(a) તેના પ્રવેગ વિશે તમે શું અનુમાન કરશો? શું તે અચળ છે, વધે છે, ઘટે છે કે શૂન્ય છે?
ઉકેલ:
કોષ્ટકમાં આપેલ સમયને અનુરૂપ પદાર્થે કાપેલ અંતરનાં મૂલ્યો પરથી સ્પષ્ટ છે કે …
t₁ = 0 s માટે s₁ = 0 m = (0)³m
t₂ = 1 s માટે s₂ = 1 m = (1)³m
t₃ = 2 s માટે s₃ = 8 m = (2)³m
t₄ = 3 s માટે s₄ = 27 m = (3)³m
t₅ = 4 s માટે s₅ = 64 m = (4)³m
…. …. …. …. …. …. …. …. ….
…. …. …. …. …. …. …. …. ….
તેથી કહી શકાય કે, s ∝ t³
→ હવે અચળ વેગી ગતિ માટે અંતર s = ut ∴ s ∝ t

→ અચળ પ્રવેગી ગતિ માટે s = ut + \(\frac{1}{2}\)at² ∴ s ∝ t²

→ પણ અહીં s ∝ t³ છે. આથી પ્રવેગ ‘a’ અચળ નથી, તે સમય છે ‘t’ પર આધારિત છે. જેમ સમય વધે છે, તેમ પ્રવેગ વધે છે.
હવે, પ્રવેગ, સમય સાથે નિયમિત રીતે વધે છે કે અનિયમિત રીતે તે ચકાસવા માટે નીચેની ગણતરી જુઓ:
આપેલ કોષ્ટક પરથી, પદાર્થની પ્રારંભિક ઝડપ u = 0 છે.
હવે, s = ut + \(\frac{1}{2}\)at²
∴ s = (0) + \(\frac{1}{2}\)at²
= \(\frac{1}{2}\)at²
∴ a = \(\frac{2 \mathrm{~s}}{t^{2}}\)

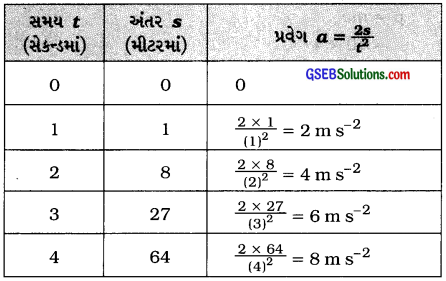
∴ સ્પષ્ટ છે કે, પ્રવેગ સમય સાથે નિયમિત રીતે વધે છે. (a = 2t)

(b) પદાર્થ પર લાગતાં બળ વિશે તમે શું અનુમાન કરશો?
ઉકેલ:
ન્યૂટનના ગતિના બીજા નિયમ F = ma પરથી F ∝ a
હવે, પ્રવેગ સમય સાથે નિયમિત રીતે વધે છે. તેથી પદાર્થ પર લાગતું બળ પણ સમય સાથે નિયમિત રીતે વધે છે.

પ્રશ્ન 2.
બે વ્યક્તિઓ 1200 kg દળ ધરાવતી કારને સુરેખ રસ્તા ? પર અચળ વેગથી ધકેલી રહી છે. જો આ જ કારને ત્રણ વ્યક્તિઓ ધકેલતી હોય, તો 0.2 m s^-2નો પ્રવેગ ઉત્પન્ન થાય છે. દરેક વ્યક્તિ કેટલા બળથી કારને ધકેલતી હશે? (દરેક વ્યક્તિ એકસરખી સ્નાયુમય તાકાત(muscular effort)થી કારને ધકેલે છે તેમ ધારો.)
ઉકેલ:
કારનું દળ m = 1200 kg
ધારો કે, એક વ્યક્તિ વડે કાર પર લાગતું બળ = F
∴ બે વ્યક્તિઓ વડે કાર પર લાગતું બળ = F + F = 2F
પરંતુ, બે વ્યક્તિઓ વડે લગાડેલ બાહ્ય બળ 2F ને લીધે સમક્ષિતિજ રસ્તા પર કાર અચળ વેગથી ગતિ કરે છે. તેથી કારનો પ્રવેગ શૂન્ય હશે.
હવે, ન્યૂટનના ગતિના બીજા નિયમ પરથી,
પરિણામી બળ = ma
∴ 2F – f = m(0) જ્યાં, f = કાર પર લાગતું ઘર્ષણબળ
∴ f = 2F
આમ, કાર પર લાગતું ઘર્ષણબળ f = 2F છે.
હવે, ત્રણ વ્યક્તિઓ દ્વારા કાર પર લાગતું બળ = F + F + F = 3F છે, જેના કારણે કાર વ = 0.2 m s^-2 જેટલા પ્રવેગથી સમક્ષિતિજ રસ્તા પર ગતિ કરે છે. તેથી ફરીથી ન્યૂટનનો ગતિનો બીજો નિયમ વાપરતાં,
પરિણામી બળ = ma
∴ 3 – f = 1200 × 0.2.
∴ 3F – F = 240
∴ F = 240 N
આમ, દરેક વ્યક્તિ કાર પર 240 N મૂલ્યનું બળ લગાડશે.

પ્રશ્ન 3.
500 g દળ ધરાવતી હથોડી 50 m s^-1ના વેગથી એક – ખીલીને અથડાય છે. ખીલી 0.01 sના ટૂંકા સમયગાળામાં હથોડીને અટકાવી દેતી હોય, તો હથોડી પર ખીલી દ્વારા લાગતું બળ કેટલું હોય?
ઉકેલ:
m = 500 g = 0.5 kg, u = 50 m/s, D = 0, 3 t = 0.01 s
હથોડીનો પ્રવેગ,
a = \(\frac{v-u}{t}\)
= \(\frac{0-50}{0.01}\)
= – 5000 m s^-2
∴ હથોડી વડે ખીલી પર લાગતું બળ,
F = ma
= 0.5 × (- 5000) = – 2500 N
ઋણ નિશાની દર્શાવે છે કે આ બળ ગતિનો વિરોધ કરે છે.
∴ બળનું મૂલ્ય |F| = 2500 N
ન્યૂટનના ગતિના ત્રીજા નિયમ પરથી, હથોડી પર ખીલી દ્વારા લાગતું બળ 2500 N છે.

પ્રશ્ન 4.
1200kg દળની એક કાર સુરેખ પથ પર 90 km h^-1ના 3 વેગથી ગતિ કરી રહી છે. બાહ્ય અસંતુલિત બળ દ્વારા તેનો વેગ 4માં ૨ ઘટીને 18 kmh1 જેટલો થાય છે, તો પ્રવેગ તથા વેગમાનમાં થતો ફેરફાર ગણો તથા જરૂરી બળનું મૂલ્ય પણ ગણો.
ઉકેલ:
અહીં, m = 1200 kg
કારનો પ્રારંભિક વેગ u = 90 km h^-1
= 90 × \(\frac{1000}{3600}\) ms^-1
= 25 m s^-1

કારનો અંતિમ વેગ v = 18 km h^-1
= 18 × \(\frac{1000}{3600}\) m s^-1
= 5 m s^-1

સમય t = 4 s
→ કારનો પ્રવેગ a = \(\frac{v-u}{t}\)
= \(\frac{5-25}{4}\) = – 5 m s^-2

→ કારના વેગમાનમાં થતો ફેરફાર

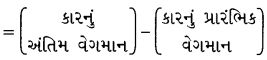
= mv – mu
= m (v – u)
= 1200 (5 – 25) kg m s^-1
= – 2400 kg m s^-1

→ કાર પર લાગતું (અસંતુલિત) બળ,
F = ma
= 1200 × (- 5)
= – 6000 N
પ્રવેગની, વેગમાનના ફેરફારની અને બળની ત્રણ નિશાની સૂચવે ૨ છે કે, બાહ્ય અસંતુલિત બળ કારની ગતિનો વિરોધ કરે છે.
∴ જરૂરી બળનું મૂલ્ય = 6000 N