GSEB Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Question 1.
(3x² – 9x + 5)⁹
Solution:
Let y = (3x² – 9x + 5)⁹ = ⁹, where u = 3x² – 9x+ 5
∴ $\frac { dy }{ dx }$ = $\frac { dy }{ du }$ x $\frac { du }{ dx }$ = 9u^9-1 x (6x – 9)
= 9(3x² – 9x + 5)⁸ . 3(2x – 3).

Question 2.
sin³ x + cos⁶x
Solution:

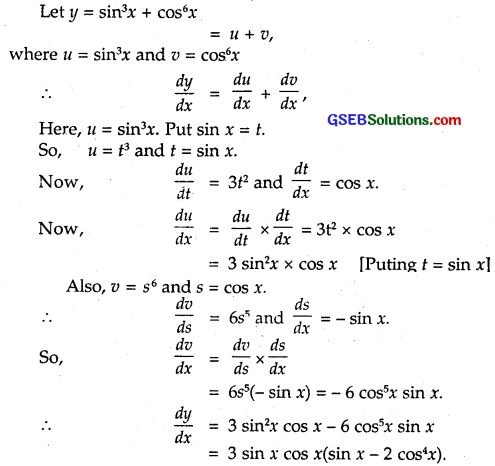
Question 3.
(5x)^{3 cos 2x}
Solution:
Let y = (5x)^{3 cos 2x}
Taking log both sides, we get
log y = 3 cos 2x log 5x
Differentiating w.r.t. x,

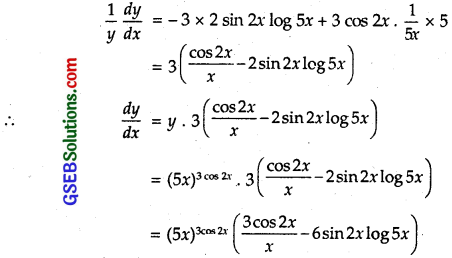
Question 4.
sin^-1(x$\sqrt{x}$), 0 ≤ x ≤ 1
Solution:

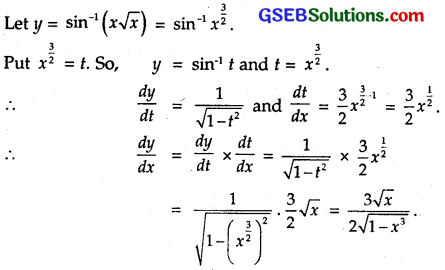
Question 5.
$\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}$, – 2 < x < 2
Solution:
Let y = $\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}$, – 2 < x < 2

Question 6.
cot^-1$\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right]$, 0 < x < $\frac { π }{ 2 }$
Solution:

Question 7.
(log x)^{log x}, x > 1
Solution:
Let (log x)^{log x}, x > 1
Taking log of both sides, we get
log y = (log x) log (log x)
Here u = log x and v = log log x.
So, = $\frac { du }{ dx }$. Also, v = log t, where t = log x.

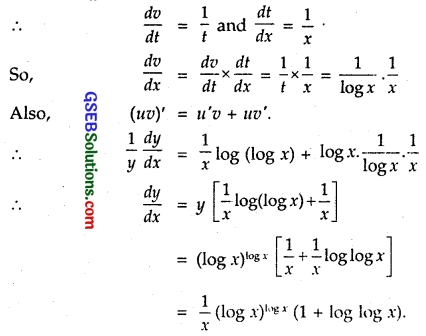
Question 8.
cos(a cos x + b sin x), for some constant a and b.
Solution:
Let cos(a cos x + b sin x).
Put a cos x + b sin x = t.

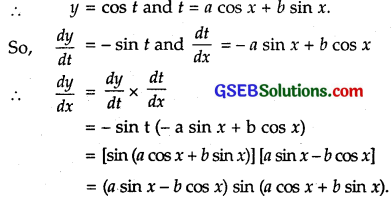
Question 9.
(sin x – cos x)^{(sin x – cos x)}, $\frac { π }{ 4 }$ < x < $\frac { 3π }{ 4 }$
Solution:
Let y = (sin x – cos x)^{sin x – cos x}
Taking log of both sides, we get
log y = (sin x – cosx)log(sin x – cos x)
Differentiating both sides w.r.t. x
$\frac { 1 }{ y }$$\frac { dy }{ dx }$ = (cos x + sin x) log (sin x – cos x) + (sin x – cos x) x $\frac { d }{ dx }$ log(sin x – cos x)
= (cos x + sin x) log (sin x – cos x) + (sin x – cos x) x $\frac { 1 }{ sin x – cos x }$ x $\frac { d }{ dx }$(sin x – cos x)
= (cos x + sin x) log (sin x – cos x) + (cos x + sin x)
= (sin x + cos x) [1 + log (sin x – cos x)]
∴ $\frac { dy }{ dx }$ = y (sin x + cos x) [1 + log (sin x – cos x)]
= (sin x + cos x) (sin x – cos x) [1 + log (sin x – cos x)^{sin x – cos x} × [1 + log (sin x – cos x)].

Question 10.
x^x + x^a + a^x + a^a, for some fixed a > 0 and x > 0.
Solution:
Let y = x^x + x^a + a^x + a^a
Differentiating w.r.t. x,

Question 11.
x^x²-3 + (x – 3)^x² for x > 3
Solution:
Let y = x^x²-3 + (x – 3)^x² = u + v.
∴ u = x^x²-3
Taking log of both sides, we get
log u = log x^x²-3 = (x² – 3) log x.
Differentiating w.r.t. x,

Question 12.
Find $\frac { dy }{ dx }$, if y = 12(1 – cos t), x = 10(t – sin t), – $\frac { π }{ 2 }$ < t < $\frac { π }{ 2}$.
Solution:

Question 13.
Find $\frac { dy }{ dx }$, if y = sin^-1x + sin^-1$\sqrt{1-x^{2}}$.
Solution:
y = sin^-1x + sin^-1$\sqrt{1-x^{2}}$.
Put x = sin θ
∴ y = θ + sin^-1$\sqrt{1-\sin ^{2} \theta}$
= θ + sin^-1 (cos θ)
= θ + $\frac { π }{ 2 }$ – θ = $\frac { π }{ 2 }$ .
∴ $\frac { dy }{ dx }$ = 0.

Question 14.
If x$\sqrt{1+y}$ + y$\sqrt{1+x}$ = 0 for – 1 < x < 1, prove that $\frac { dy }{ dx }$ = – $\frac{1}{(1+x)^{2}}$
Solution:
The given equation may be written as
x$\sqrt{1+y}$ = – y$\sqrt{1+x}$
Squaring both sides, we get,
x²(1 + y) = y²(1 + x) ⇒ x² – y² = y² x – x²y
⇒ (x + y) (x – y) = – xy(x – y)
⇒ x + y = – xy [∵ x – y ≠ 0 ]
⇒ x = – y – xy
⇒ y(1 + x) = – x
⇒ y = – $\frac { x }{ 1+x }$
⇒ $\frac { dy }{ dx }$ = – $\left\{\frac{(1+x) \cdot 1-x(0+1)}{(1+x)^{2}}\right\}$
⇒ $\frac { dy }{ dx }$ = – $\frac{1}{(1+x)^{2}}$

Question 15.
If (x – a)² + (y – b)² = c², for some c > 0, prove that $\frac{\left\{1+\left(\frac{d y}{d x}\right)^{2}\right\}^{3 / 2}}{\frac{d^{2} y}{d x^{2}}}$ is a constant, independent of a and b.
Solution:
Given (x – a)² + (y – b)² = c² … (1)
Differentiating (1) w.r.t. x, we get
2(x – a) + 2(y – b)$\frac { dy }{ dx }$ = 0
⇒ (x – a) + (y – b)$\frac { dy }{ dx }$ = 0 … (2)
Differentiating (2) w.r.t. x, we get
1 + (y – b) . $\frac{d^{2} y}{d x^{2}}$ + ($\frac { dy }{ dx }$)² = 0

Putting these values of (y-b) and (x – a) from (3) and (4) in (1), we get

which is a constant, independent of a and b.

Question 16.
If cos y = x cos (a + y), with cos a ≠ ± 1, prove that $\frac { dy }{ dx }$ = $\frac{\cos ^{2}(a+y)}{\sin a}$
Solution:
Given: cos y = x cos (a + y).

Question 17.
If x = a (cos t + t sin t) and y = a (sin t – 1 cos t), find $\frac{d^{2} y}{d x^{2}}$. Mention the domain in which it is valid.
Solution:
We have : x = a (cos t + t sin t)
∴ $\frac { dx }{ dt }$ = a (- sin t + sin t + t cos t) = at cos t.
Also, we have : y = a (sin t – t cos t)
∴ $\frac { dy }{ dx }$ = a(cos t – cos t + t sin t) = at sin t.
∴ $\frac { dy }{ dx }$ = $\frac{\frac{d y}{d t}}{\frac{d x}{d t}}$ = $\frac{a t \sin t}{a t \cos t}$ = tan t.
It is valid when t ≠ 0, t ≠ (2n + 1)$\frac { π }{ 2 }$.

Here, also t ≠ 0, t ≠ (2n + 1)$\frac { π }{ 2 }$,
So, domain is t ∈R – [ (2n + 1)$\frac { π }{ 2 }$ ].

Question 18.
If f(x) = | x |³, show that f”(x) exists for all real x and find it.
Solution:
When x ≥ 0, then f(x) = | x |³ = x³.
∴ f’ (x) = – 3x² and f”(x) = 6x, which exists for all real values of x.
When x < 0, then
f(x) = | x |³ = (- x)³ = – x³.
∴ f'(x) = – 3x²
and f”(x) = – 6x,
which exists for all real values of x.
Hence, f'”(x) = $\left\{\begin{array}{r} 6 x, \text { if } x \geq 0 \\ -6 x, \text { if } x<0 \end{array}\right.$

Question 19.
Using Mathematical Induction, prove that $\frac { d }{ dx }$(xⁿ) = nx^n-1, ∀ n ∈ N, for all positive integers n.
Solution:
Let P(n) be the given statement in the problem.
∴ P(n) : $\frac { d }{ dx }$(xⁿ) = nx^n-1 … (1)
To verify the statement for n = 1,
put n = 1 in (1). We get
P(1) : $\frac { d }{ dx }$(x¹) = (1)x^1-1 = (1)(x)⁰ = (1)(1) = 1,
which is true as $\frac { d }{ dx }$ (x) = 1.
We suppose P(x) is true for n = m.
∴ P(m) : $\frac { d }{ dx }$(x^m) = m x^m-1 … (2)
To establish the truth of P(m + 1), we prove
P(m + 1) : $\frac { d }{ dx }$(x^m+1) = (m + 1) x^m.
Since x^m+1 = x¹. x^m
∴ $\frac { d }{ dx }$(x^m+1) = $\frac { d }{ dx }$(x . x^m) = x $\frac { d }{ dx }$(x^m) + x^m $\frac { d }{ dx }$ (x)
= x . mx^m-1 + x^m . 1 [Using (2)]
= mx^m + x^m = (m + 1)x^m
= (m + 1) x^(m+1)-1.
∴ p(m + 1) is also true, if P(m) is true. But P(1) is true.
∴ By principle of mathematical induction, P(n) is true for all n ∈ N.

Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Solution:
sin (A + B) = sin A cos B + cos A sin B … (1)
Consider A and B as functions of t and differentiating both sides of (1) w.r.t. t, we have:

Question 21.
Does there exist a function which is continuous every-where but not differentiable at exactly two points? Justify your answer.
Solution:
Consider the function
f(x) = | x | + |x-1|
f is continuous everywhere. But it is not differentiable at x – 0 and x = 1.

Question 22.
If y = $\left|\begin{array}{ccc} f(x) & g(x) & h(x) \\ l & m & n \\ a & b & c \end{array}\right|$, prove that $\left|\begin{array}{ccc} f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\ l & m & n \\ a & b & c \end{array}\right|$
Solution:
To differentiate a determinant, we differentiate one row (or one column) at a time, keeping other unchanged.

Question 23.
If y = $e^{a \cos ^{-1} x}$, show that (1 – x²)$\frac{d^{2} y}{d x^{2}}$ – x$\frac { dy }{ dx }$ – a²y = 0
Solution:
We have :