Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Miscellaneous Exercise
![]()
Question 1.
(3x² – 9x + 5)9
Solution:
Let y = (3x² – 9x + 5)9 = 9, where u = 3x² – 9x+ 5
∴ \(\frac { dy }{ dx }\) = \(\frac { dy }{ du }\) x \(\frac { du }{ dx }\) = 9u9-1 x (6x – 9)
= 9(3x² – 9x + 5)8 . 3(2x – 3).
Question 2.
sin3 x + cos6x
Solution:
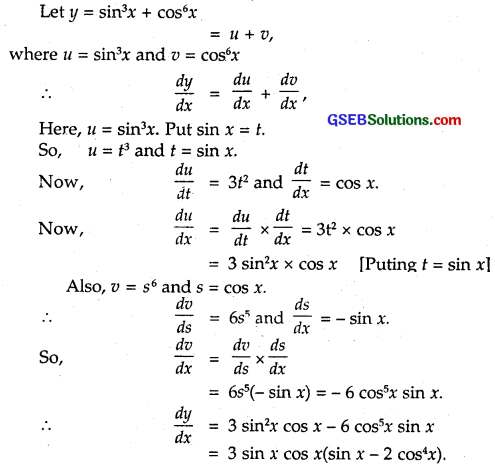
![]()
Question 3.
(5x)3 cos 2x
Solution:
Let y = (5x)3 cos 2x
Taking log both sides, we get
log y = 3 cos 2x log 5x
Differentiating w.r.t. x,
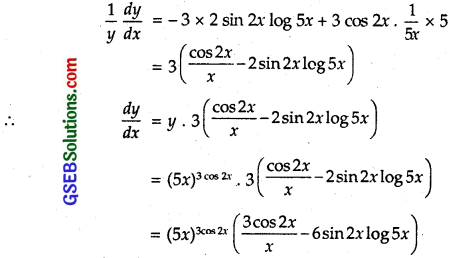
Question 4.
sin-1(x\(\sqrt{x}\)), 0 ≤ x ≤ 1
Solution:
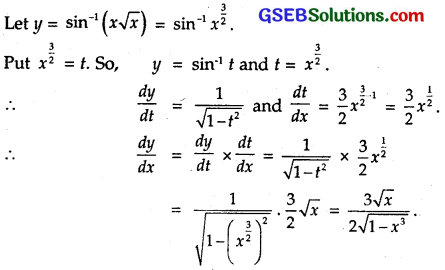
Question 5.
\(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}\), – 2 < x < 2
Solution:
Let y = \(\frac{\cos ^{-1} \frac{x}{2}}{\sqrt{2 x+7}}\), – 2 < x < 2

Question 6.
cot-1\(\left[\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right]\), 0 < x < \(\frac { π }{ 2 }\)
Solution:

Question 7.
(log x)log x, x > 1
Solution:
Let (log x)log x, x > 1
Taking log of both sides, we get
log y = (log x) log (log x)
Here u = log x and v = log log x.
So, = \(\frac { du }{ dx }\). Also, v = log t, where t = log x.
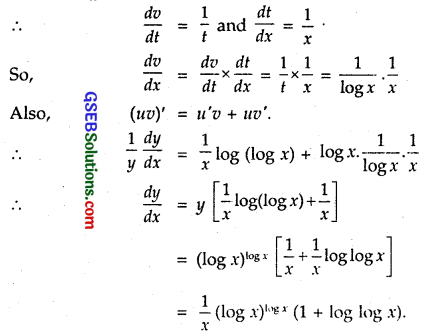
Question 8.
cos(a cos x + b sin x), for some constant a and b.
Solution:
Let cos(a cos x + b sin x).
Put a cos x + b sin x = t.
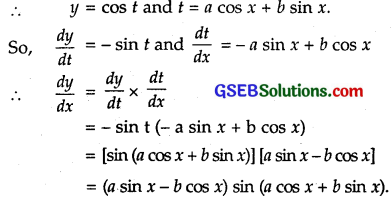
Question 9.
(sin x – cos x)(sin x – cos x), \(\frac { π }{ 4 }\) < x < \(\frac { 3π }{ 4 }\)
Solution:
Let y = (sin x – cos x)sin x – cos x
Taking log of both sides, we get
log y = (sin x – cosx)log(sin x – cos x)
Differentiating both sides w.r.t. x
\(\frac { 1 }{ y }\)\(\frac { dy }{ dx }\) = (cos x + sin x) log (sin x – cos x) + (sin x – cos x) x \(\frac { d }{ dx }\) log(sin x – cos x)
= (cos x + sin x) log (sin x – cos x) + (sin x – cos x) x \(\frac { 1 }{ sin x – cos x }\) x \(\frac { d }{ dx }\)(sin x – cos x)
= (cos x + sin x) log (sin x – cos x) + (cos x + sin x)
= (sin x + cos x) [1 + log (sin x – cos x)]
∴ \(\frac { dy }{ dx }\) = y (sin x + cos x) [1 + log (sin x – cos x)]
= (sin x + cos x) (sin x – cos x) [1 + log (sin x – cos x)sin x – cos x × [1 + log (sin x – cos x)].
![]()
Question 10.
xx + xa + ax + aa, for some fixed a > 0 and x > 0.
Solution:
Let y = xx + xa + ax + aa
Differentiating w.r.t. x,

Question 11.
xx²-3 + (x – 3)x² for x > 3
Solution:
Let y = xx²-3 + (x – 3)x² = u + v.
∴ u = xx²-3
Taking log of both sides, we get
log u = log xx²-3 = (x² – 3) log x.
Differentiating w.r.t. x,

Question 12.
Find \(\frac { dy }{ dx }\), if y = 12(1 – cos t), x = 10(t – sin t), – \(\frac { π }{ 2 }\) < t < \(\frac { π }{ 2}\).
Solution:

![]()
Question 13.
Find \(\frac { dy }{ dx }\), if y = sin-1x + sin-1\(\sqrt{1-x^{2}}\).
Solution:
y = sin-1x + sin-1\(\sqrt{1-x^{2}}\).
Put x = sin θ
∴ y = θ + sin-1\(\sqrt{1-\sin ^{2} \theta}\)
= θ + sin-1 (cos θ)
= θ + \(\frac { π }{ 2 }\) – θ = \(\frac { π }{ 2 }\) .
∴ \(\frac { dy }{ dx }\) = 0.
Question 14.
If x\(\sqrt{1+y}\) + y\(\sqrt{1+x}\) = 0 for – 1 < x < 1, prove that \(\frac { dy }{ dx }\) = – \(\frac{1}{(1+x)^{2}}\)
Solution:
The given equation may be written as
x\(\sqrt{1+y}\) = – y\(\sqrt{1+x}\)
Squaring both sides, we get,
x²(1 + y) = y²(1 + x) ⇒ x² – y² = y² x – x²y
⇒ (x + y) (x – y) = – xy(x – y)
⇒ x + y = – xy [∵ x – y ≠ 0 ]
⇒ x = – y – xy
⇒ y(1 + x) = – x
⇒ y = – \(\frac { x }{ 1+x }\)
⇒ \(\frac { dy }{ dx }\) = – \(\left\{\frac{(1+x) \cdot 1-x(0+1)}{(1+x)^{2}}\right\}\)
⇒ \(\frac { dy }{ dx }\) = – \(\frac{1}{(1+x)^{2}}\)
Question 15.
If (x – a)² + (y – b)² = c², for some c > 0, prove that \(\frac{\left\{1+\left(\frac{d y}{d x}\right)^{2}\right\}^{3 / 2}}{\frac{d^{2} y}{d x^{2}}}\) is a constant, independent of a and b.
Solution:
Given (x – a)² + (y – b)² = c² … (1)
Differentiating (1) w.r.t. x, we get
2(x – a) + 2(y – b)\(\frac { dy }{ dx }\) = 0
⇒ (x – a) + (y – b)\(\frac { dy }{ dx }\) = 0 … (2)
Differentiating (2) w.r.t. x, we get
1 + (y – b) . \(\frac{d^{2} y}{d x^{2}}\) + (\(\frac { dy }{ dx }\))² = 0

Putting these values of (y-b) and (x – a) from (3) and (4) in (1), we get

which is a constant, independent of a and b.
![]()
Question 16.
If cos y = x cos (a + y), with cos a ≠ ± 1, prove that \(\frac { dy }{ dx }\) = \(\frac{\cos ^{2}(a+y)}{\sin a}\)
Solution:
Given: cos y = x cos (a + y).

Question 17.
If x = a (cos t + t sin t) and y = a (sin t – 1 cos t), find \(\frac{d^{2} y}{d x^{2}}\). Mention the domain in which it is valid.
Solution:
We have : x = a (cos t + t sin t)
∴ \(\frac { dx }{ dt }\) = a (- sin t + sin t + t cos t) = at cos t.
Also, we have : y = a (sin t – t cos t)
∴ \(\frac { dy }{ dx }\) = a(cos t – cos t + t sin t) = at sin t.
∴ \(\frac { dy }{ dx }\) = \(\frac{\frac{d y}{d t}}{\frac{d x}{d t}}\) = \(\frac{a t \sin t}{a t \cos t}\) = tan t.
It is valid when t ≠ 0, t ≠ (2n + 1)\(\frac { π }{ 2 }\).

Here, also t ≠ 0, t ≠ (2n + 1)\(\frac { π }{ 2 }\),
So, domain is t ∈R – [ (2n + 1)\(\frac { π }{ 2 }\) ].
![]()
Question 18.
If f(x) = | x |³, show that f”(x) exists for all real x and find it.
Solution:
When x ≥ 0, then f(x) = | x |³ = x³.
∴ f’ (x) = – 3x² and f”(x) = 6x, which exists for all real values of x.
When x < 0, then
f(x) = | x |³ = (- x)³ = – x³.
∴ f'(x) = – 3x²
and f”(x) = – 6x,
which exists for all real values of x.
Hence, f'”(x) = \(\left\{\begin{array}{r} 6 x, \text { if } x \geq 0 \\ -6 x, \text { if } x<0 \end{array}\right.\)
Question 19.
Using Mathematical Induction, prove that \(\frac { d }{ dx }\)(xn) = nxn-1, ∀ n ∈ N, for all positive integers n.
Solution:
Let P(n) be the given statement in the problem.
∴ P(n) : \(\frac { d }{ dx }\)(xn) = nxn-1 … (1)
To verify the statement for n = 1,
put n = 1 in (1). We get
P(1) : \(\frac { d }{ dx }\)(x1) = (1)x1-1 = (1)(x)0 = (1)(1) = 1,
which is true as \(\frac { d }{ dx }\) (x) = 1.
We suppose P(x) is true for n = m.
∴ P(m) : \(\frac { d }{ dx }\)(xm) = m xm-1 … (2)
To establish the truth of P(m + 1), we prove
P(m + 1) : \(\frac { d }{ dx }\)(xm+1) = (m + 1) xm.
Since xm+1 = x1. xm
∴ \(\frac { d }{ dx }\)(xm+1) = \(\frac { d }{ dx }\)(x . xm) = x \(\frac { d }{ dx }\)(xm) + xm \(\frac { d }{ dx }\) (x)
= x . mxm-1 + xm . 1 [Using (2)]
= mxm + xm = (m + 1)xm
= (m + 1) x(m+1)-1.
∴ p(m + 1) is also true, if P(m) is true. But P(1) is true.
∴ By principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
Question 20.
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
Solution:
sin (A + B) = sin A cos B + cos A sin B … (1)
Consider A and B as functions of t and differentiating both sides of (1) w.r.t. t, we have:

Question 21.
Does there exist a function which is continuous every-where but not differentiable at exactly two points? Justify your answer.
Solution:
Consider the function
f(x) = | x | + |x-1|
f is continuous everywhere. But it is not differentiable at x – 0 and x = 1.
![]()
Question 22.
If y = \(\left|\begin{array}{ccc}
f(x) & g(x) & h(x) \\
l & m & n \\
a & b & c
\end{array}\right|\), prove that \(\left|\begin{array}{ccc}
f^{\prime}(x) & g^{\prime}(x) & h^{\prime}(x) \\
l & m & n \\
a & b & c
\end{array}\right|\)
Solution:
To differentiate a determinant, we differentiate one row (or one column) at a time, keeping other unchanged.

Question 23.
If y = \(e^{a \cos ^{-1} x}\), show that (1 – x²)\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac { dy }{ dx }\) – a²y = 0
Solution:
We have :
