This GSEB Class 8 Maths Notes Chapter 3 ચતુષ્કોણની સમજ covers all the important topics and concepts as mentioned in the chapter.
ચતુષ્કોણની સમજ Class 8 GSEB Notes
→ કાગળ એ એક સમતલની પ્રતિકૃતિ છે.
→ કાગળ ઉપર જુદાં જુદાં બિંદુઓ મૂકી તેને પેન્સિલ વડે જોડતાં સમતલીય વક્ર મળે છે.
→ ફક્ત રેખાખંડોથી બનેલા સાદા બંધ વક્રને બહુકોણ કહે છે.
→ બહુકોણનાં ઉદાહરણ : ત્રિકોણ, ચતુષ્કોણ, પંચકોણ, ષટ્કોણ, સપ્તકોણ, અષ્ટકોણ, … છે.
→ બહિર્મુખ બહુકોણમાં તેના વિકર્ણનો કોઈ પણ ભાગ બહુકોણના બહારના ભાગમાં હોતો નથી. અંતર્મુખ ચતુષ્કોણમાં આવું હોતું નથી.
![]()
→ નિયમિત બહુકોણમાં તેની બધી જ બાજુઓનાં માપ સરખાં હોય છે.
→ ચતુષ્કોણમાં બધા ખૂણાઓનાં માપનો સરવાળો 360° થાય
→ કોઈ પણ બહુકોણના બહિષ્કોણોનાં માપનો સરવાળો 360° થાય છે.
→ ત્રિકોણના બહિષ્કોણનાં માપનો સરવાળો = 360°
ચતુષ્કોણના બહિષ્કોણનાં માપનો સરવાળો = 360°
પંચકોણના, ષટ્કોણના, … બહિષ્કોણોનાં માપનો સરવાળો = 360°
→ ચતુષ્કોણના પ્રકારોઃ
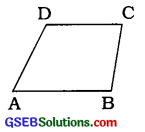
(1) સમલંબ ચતુષ્કોણ: જે ચતુષ્કોણમાં સામસામેની બાજુઓની ફક્ત એક જ જોડની બાજુઓ સમાંતર હોય તે ચતુષ્કોણને સમલંબ ચતુષ્કોણ કહે છે. જુઓ અહીં □ABCD એ સમલંબ ચતુષ્કોણ છે.
□ABCDમાં \(\overline{\mathrm{AB}}\) ∥ \(\overline{\mathrm{CD}}\) છે.
(2) પતંગ (પતંગાકાર ચતુષ્કોણ):
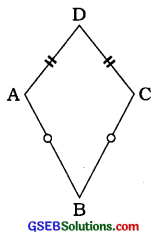
જે ચતુષ્કોણમાં પાસપાસેની બાજુઓની બે અલગ અલગ જોડ સરખી હોય તે ચતુષ્કોણને પતંગ , (પતંગાકાર ચતુષ્કોણ) કહે છે. અહીં □ABCD એ પતંગ (પતંગાકાર ચતુષ્કોણ) છે.
□ABCD માં AB = BC અને CD = DA છે.
(3) સમાંતરબાજુ ચતુષ્કોણ?
જે ચતુષ્કોણમાં સામસામેની બાજુઓ સમાન અને સમાંતર હોય તે ચતુષ્કોણને સમાંતરબાજુ ચતુષ્કોણ કહે છે.
અહીં □ABCD એ સમાંતરબાજુ ચતુષ્કોણ છે.
આ □ABCDમાં AB = CD 24È \(\overline{\mathrm{AB}}\) ∥ \(\overline{\mathrm{CD}}\)
તથા AD = BC અને \(\overline{\mathrm{AB}}\) ∥ \(\overline{\mathrm{CD}}\)
→ સમાંતરબાજુ ચતુષ્કોણના સામસામેના ખૂણા સમાન હોય છે.
→ સમાંતરબાજુ ચતુષ્કોણમાં પાસપાસેના ખૂણા એકબીજાના પૂરક હોય છે.
→ સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર દુભાગે છે.
→ વિશિષ્ટ સમાંતરબાજુ ચતુષ્કોણોઃ
(1) સમબાજુ ચતુષ્કોણ જે સમાંતરબાજુ ચતુષ્કોણની ચારે બાજુઓનાં માપ સમાન હોય, તે ચતુષ્કોણને સમબાજુ ચતુષ્કોણ કહે છે.
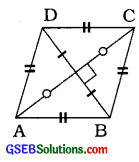
અહીં, સમાંતરબાજુ □ABCDમાં
AB = BC = CD = DA છે.
□ABCD સમબાજુ ચતુષ્કોણ છે.
→ સમબાજુ ચતુષ્કોણના વિકણોં પરસ્પર કાટખૂણે દુભાગે છે.
(2) ચોરસ જે સમાંતરબાજુ ચતુષ્કોણની ચારે બાજુઓનાં માપ સમાન હોય,
અને ચારે ખૂણા કાટખૂણા હોય તે ચતુષ્કોણને ચોરસ કહે છે.
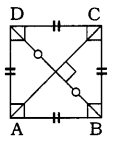
અહીં, સમાંતરબાજુ □ABCDમાં
AB = BC = CD = DA તથા
m∠A = m∠B = m∠C = m∠D = 90° છે.
□ABCD ચોરસ છે.
→ચોરસના વિકણોં પરસ્પર કાટખૂણે દુભાગે છે.
![]()
→ચોરસના વિકણનાં માપ સરખાં હોય છે. અહીં AC = BD
(3) લંબચોરસ જે સમાંતરબાજુ ચતુષ્કોણની સામ-સામેની બાજુઓનાં માપ સમાન હોય અને ચારે ખૂણા કાટખૂણા હોય તે ચતુષ્કોણને લંબચોરસ ) કહે છે. અહીં, સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB = CD અને BC = DA છે તથા m∠A = m∠B = m∠C = m∠D = 90° છે.
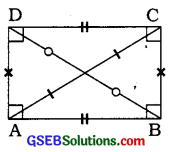
□ABCD એ લંબચોરસ છે.
→ લંબચોરસના વિકણ પરસ્પર દુભાગે છે.
→ લંબચોરસના વિકર્ણોનાં માપ સરખાં હોય છે. અહીં AC = BD હોય.