GSEB Class 9 Maths Notes Chapter 1 Number Systems

This GSEB Class 9 Maths Notes Chapter 1 Number Systems covers all the important topics and concepts as mentioned in the chapter.

Number Systems Class 9 GSEB Notes

Natural numbers:
The numbers 1, 2, 3, 4, ……. are called natural numbers. The collection of all these numbers is the collection of natural numbers. It is denoted by N.

• Thus, N = {1, 2, 3, …….}
• The smallest natural number is 1, but there is no greatest natural number. There are infinitely many natural numbers.
• For natural numbers a and b, a < b, there lies (b – a – 1) natural numbers between a and b.

Whole numbers:
The collection of all the natural numbers and 0 is called the collection of whole numbers. It is denoted by W.

• Thus, W = {0, 1, 2, 3, …}
• The smallest whole number is 0, but there is no greatest whole number. There are infinitely many whole numbers.
• For whole numbers a and b, a < b, there lies (b – a – 1) whole numbers between a and b.

Integers:
The collection of all the natural numbers, their opposites and 0 is called the collection of integers. It is denoted by Z.

• Thus, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
• The symbol Z comes from the German word ‘zahlen’ which means ‘to count’.
• There is neither the smallest nor the greatest integer. There are infinitely many integers.
• For integers a and b, a < b, there lies (b – a – 1) integers between a and b.

Rational numbers:
The numbers of the form \(\frac{p}{q}\); where p and q are integers, q ≠ 0, are called rational numbers. The collection of rational numbers is denoted by Q.

→ A number r is called a rational number, if it can be written in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.

→ The word ‘rational’ comes from the word ‘ratio’ and Q comes from the word ‘quotient’.

→ These is neither the smelliest nor the greatest rational number. There are infinitely many rational numbers.
Rational numbers do not have a unique representation in the form \(\frac{p}{q} \cdot \frac{1}{4}, \frac{2}{8}, \frac{3}{12}, \frac{4}{16}\) are all the representation of the same rational number \(\frac{1}{4}\). They are called equivalent rational numbers.

→ When we want to represent \(\frac{p}{q}\) on the number line, we assume that p and q have no common factor other than 1, i.e., p and q are co-prime.

→ There are infinitely many rational numbers between two distinct rational numbers. This is one important property of Q. This property is referred as ‘The rational numbers exhibit gap’.

→ Any natural number is also a rational number, e.g., 7 = \(\frac{7}{1}\). The same holds good for whole numbers and integers.

→ The decimal representation of a rational number is either terminating or non¬terminating recurring.

Rational numbers between two given distinct rational numbers:
There are different methods to find the required number of rational numbers between two given rational numbers.

• Let a and b be rational numbers, a < b. Then, the average of a and b, i.e., \(\frac{a+b}{2}\) is one rational number between a and b as a < \(\frac{a+b}{2}\) < b. This procedure can be extended to find the required number of rational numbers between a and b.
• Express a and b with like (same) denominator and then take their equivalent rational numbers depending on the number of rational numbers to be found between them.
• Express a and b in their decimal forms and then increase the decimal places by adding zeros to the right as required depending on the number of rational numbers to be found between them.

Example 1:
Are the following statements true or false?
Give reasons for your answers:
(i) Every whole number is a natural number.
Answer:
The given statement Is false, because zero is a whole number but not a natural number.

(ii) Every integer is a rational number.
Answer:
The given statement is true, because every Integer m can be expressed in the form \(\frac{m}{1}\) and so It Is a rational number.

(iii) Every rational number is an integer.
Answer:
The given statement Is false, because \(\frac{3}{5}\) is a rational number but not an integer.

Example 2:
Find five rational numbers between 1 and 2.
Method 1:
To find a rational number between r and s, we can add r and s and divide the sum by 2, that is \(\frac{r+s}{2}\) lies between r and s. So, Is a number between 1 and 2. We can proceed In this manner to find four more rational numbers between 1 and 2. These four numbers are \(\frac{5}{4}, \frac{11}{8}, \frac{13}{8}\) and \(\frac{7}{4}\)

Method 2:
The other option Is to find all the five rational numbers In one step. Since we want five numbers, we write 1 and 2 as rational numbers with denominator 6(5 + 1). i.e., 1 = \(\frac{6}{6}\) and 2 = \(\frac{12}{6}\). Then we can easily sëe that \(\frac{7}{6}, \frac{8}{6}, \frac{9}{6}, \frac{10}{6}\) and \(\frac{11}{6}\) are all rational numbers between 1 and 2. So, the five required numbers are \(\frac{7}{6}, \frac{4}{3}, \frac{3}{2}, \frac{5}{3}\) and

Remark: In fact, there are infinitely many rational numbers between 1 and 2. We were asked to find only five. So. depending upon the method applied, we get different numbers.

Irrational number:
A number s Is called Irrational, if it cannot be written In the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.

• A number, which Is not a rational number is called an irrational number. In other words, a number, whose decimal form Is neither terminating nor non-terminating recurring, Is called an irrational number. An irrational number cannot be expressed in form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
• The numbers like, \(\sqrt{2}, \sqrt{3}, \sqrt[3]{10}\), etc. are irrational numbers.
• The decimal form of an irrational number is non-terminating (infinite) non-recurring like 0.01001000100001 …..

Real numbers:
The collection of all the rational numbers and the irrational numbers is called the collection of real numbers. It is represented by R.
The irrational numbers of the form \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) etc. (i.e., square root of a natural number) can be represented on the number line with the help of Pythagoras’ theorem. For this, we can express a number as the sum of squares of not just two numbers, but even more than two numbers.

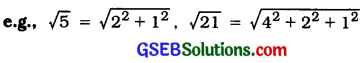
Every real number is represented by a unique point on the number line and every point on the number line represents a unique real number. Hence, the number line is called real number line.

Example 1:
Locate \(\sqrt{2}\) on the number line. Consider a square OABC, with C B

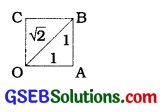
each side 1 unIt In length (see figure). Then you can see by \(\sqrt{2}\) the Pythagoras’ theorem that Figure
OB = \(\sqrt{1^{2}+1^{2}}=\sqrt{2}\) = How do we represent \(\sqrt{2}\) on the number Une? This is easy. Transfer figure onto the number line making sure that the vertex O coincides with zero (see figure below).

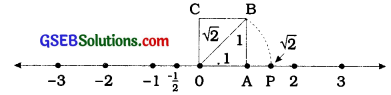
We have just seen that OB = \(\sqrt{2}\). Using a compass draw an arc with centre O and radius OB, intersecting the number line at the point P Then. P corresponds to \(\sqrt{2}\) on the number line.

Example 2:
Locate \(\sqrt{3}\) on the number line.
Answer:
Let us return to the previous figure.

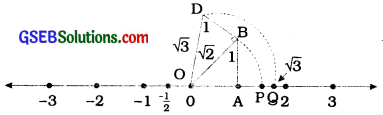
Construct BD of unit length perpendicular to OB (as in the figure). Then using the Pythagoras’ theorem, we see that OD = \(\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{3}\) Using a compass draw an arc with centre O and radius OD, which Intersects the number line at the point Q. Then, Q corresponds to \(\sqrt{2}\).

In the same way, we can locate for any positive integer n, after \(\sqrt{n-1}\) has been located.

Real numbers and their decimal expansion:
To obtain the decimal expansion of rational number \(\frac{p}{q}\), we divide p by q. On dividing p by q, we come across two situations:
1. When the division terminates: Consider rational number \(\frac{5}{8}\). Its decimal expansion can be obtained by dividing 5 by 8 as follows:

Here, lite division terminates after certain stage and the remainder becomes zero. This type of decimal expansion is called terminating decimal.

2. When the division does not terminate: Consider rational number \(\frac{5}{7}\)

Here, the division does not terminate but continues on and on. After certain stages, the same remainder appears. Similarly, certain digits In the same order appear. In the quotient. Here, the remainders 1, 3, 2, 6, 4 and 5 repeat in that order and the digits 7. 1. 4, 2, 8 and 5 repeat In that order In the quotient. This type of decimal expansion is called non-terminating recurring decimal.

This type of decimal expansion is called non-terminating recurring decimal.

Note: If a non-terminating recurring decimal number is o.m, then its \(\frac{p}{q}\) form is \(\frac{m}{9}\)

Similarly, \(0 . \overline{m n}=\frac{m n}{99}\)
\(0 . \overline{m n r}=\frac{m n r}{999}\) and so on.

→ b If In the decimal part of a number few digits are recurring and others are not recurring. Its form can be obtained easily as follows:
a . b\(\overline{c d}\) = \(\frac{p}{q}\) where

→ p = the number formed by all digits excluding decimal point – the number formed by non..recurring digits excluding decimal point.
i.e., p = abcd – ab

→ q = as many 9s as the number of recurring digits followed by as many 0s as the number of non-recurring digits in the decimal part.
i.e., q = 990

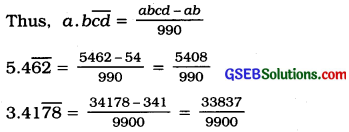
→ Thus, a number Is rational If and only If Its decimal expansion Is terminating or non-terminating recurring.

→ This clearly means that the decimal expansion of a rational number is either terminating or non-terminaüng recurring. Conversely, a number whose decimal expansion is either terminating or non-terminating recurring Is a rational number.

→ Obvlously a number is irrational if and only if its decimal expansion is non-terminating and non-recurring.

→ This clearly means that the decimal expansion of an irrational number Is non-terminating, non-recurring. Conversely, a number whose decimal expansion is non-terminating non-recurring Is an Irrational number.

→ Any decimal number, either terminating or non-terminating recurring, can be converted to \(\frac{p}{q}\) form easily.

→ The decimal expansion of \(\frac{p}{q}\) is terminating if q = 2^m5ⁿ, where m and n are whole numbers. The decimal expansion of \(\frac{p}{q}\) is non-terminating recurring If q has at least one factor other than 2 and 5.

→ Just like rational numbers, real numbers also exhibit gap. Meaning that there are infinitely many real numbers between any two given real numbers.

→ π Is an irrational number, \(\frac{22}{7}\) and 3.14 are approximations of π to be used in practical problems.

Example 1:
Find the decimal expansions of \(\frac{10}{3}, \frac{7}{8}\) and \(\frac{1}{7}\).


Remalnders:3, 2, 6. 4. 5, 1, 3, 2, 6. 4, 5, 1,…
Divisor: 7 ∴ \(\frac{1}{7}\) = \(0 . \overline{142857}\)

Example 2:
Show that 3.142678 is a rational number. In other words, express 3.142678 in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Answer:
We have 3.142678 = \(\frac{3142678}{1000000}\), and hence Is a rational number.

Example 3:
Show that 0.3333 … = 0.3̅ can be expressed in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Let x = 0.3333…
∴ 10x = 10 x (0.3333 …) = 3.3333 …
Now, 3.3333 … = 3 + x, since x = 0.3333 …
∴ 10x = 3 + x
Solving for x, we get 9x = 3, i.e., x = \(\frac{1}{3}\)
∴ 0.3̅ = \(\frac{1}{3}\)

Example 4:
Show that 1.272727 … = \(1 . \overline{27}\) can be expressed in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0.
Answer:
Let x = 1.272727 …
Since two digits are repeating. we multiply x by 100 to get
100x= 127.2727…
∴ 100x = 126+ 1.2727… = 126 + x
∴100x – x = 126, i.e., 99x = 126
∴ x = \(\frac{126}{99}=\frac{14}{11}\)
Thus, \(1 . \overline{27}=\frac{14}{11}\)

Example 5:
Show that 0.2353535 … = \(0.2 \overline{35}\) can be expressed In the form where p and q are integers and q ≠ 0.
Answer:
Let x = 0.2
Over here, note that 2 does not repeat, but the block 35 repeats. Since two digits are repeating, we multiply x by 100 to get
100x = 23.53535 …
∴ 100x = 23.3 + 0.23535 … = 23.3 + x
∴ 99x = 23.3
∴ 99x = \(\frac{233}{10}\) which gives x = \(\frac{233}{990}\)
Thus, \(0.2 \overline{35}=\frac{233}{990}\)

Example 6:
Find an irrational number between \(\frac{1}{7}\) and \(\frac{2}{7}\)
Answer:
We know that \(\frac{1}{7}=0 . \overline{142857}\) So, we can
easily calculate \(\frac{2}{7}=0 . \overline{285714}\) = 0.285714.
To find an irrational number between \(\frac{1}{7}\) and \(\frac{2}{7}\), we find a number which is non-terminating non-recurring and lying between \(0. \overline{142857}\) and \(0. \overline{285714}\). There are infinitely many such numbers. We can state 0.150150015000150000 …… as one such number.

Representing real numbers on the number line:
We can express any real number in the decimal form. After writing the real number into decimal form, it is easy to locate it on the number line. For this purpose, we use the ‘process of successive magnification’. The number of successive magnifications will increase with the increase in the decimal places of the real number. Following figures will explain the ‘process of successive magnification’ where number 2.347 is represented on the number line :

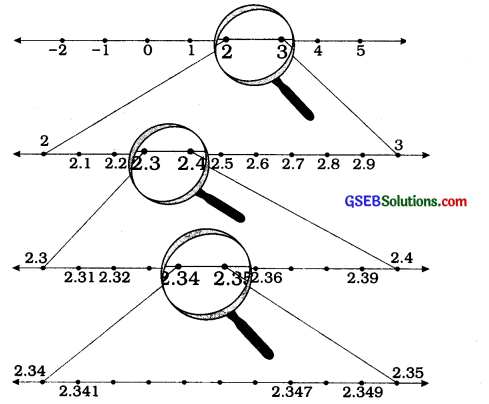
→ Similarly, we can locate non-terminating recurring decimal numbers on the number line up to whatever number of decimal places we wish to.

→ Moreover, we can as well locate non-terminating non-recurring numbers on the number line up to the required number of decimal places.

→ Every real number is represented by a unique point on the number line and every point on the number line represents one and only one (unique) real number.

Example 1:
Visualize the representation of 5.37̅ on the number line up to 5 decimal places, that is, up to 5.37777
Answer:
Once again we proceed by successive magnification, and successively decrease the lengths of the portions of the number line In which 5.37̅ Is located. First, we see that 5.37̅ Is located between 5 and 6. In the next step, we locate 5.37̅ between 5.3 and 5.4. To get a more accurate visualization of the representation, we divide this portion of the number line Into 10 equal parts and use a magnifying glass to visualize that 5.37̅ lies between 5.37 and 5.38. To visualize 5.37̅ more accurately, we again divide the portion between 5.37 and 5.38 Into ten equal parts and use a magnifying glass to visualize that 5.3 lies between 5.377 and 5.378.

Now to visualize 5.37̅ still more accurately, we divide the portion between 5.377 and 5.378 into 10 equal parts, and visualize the representation of 5.37 as In figure 4. NotIce that 5.37 Is located closer to 5.3778 than to 5.3777 (see figure 4).

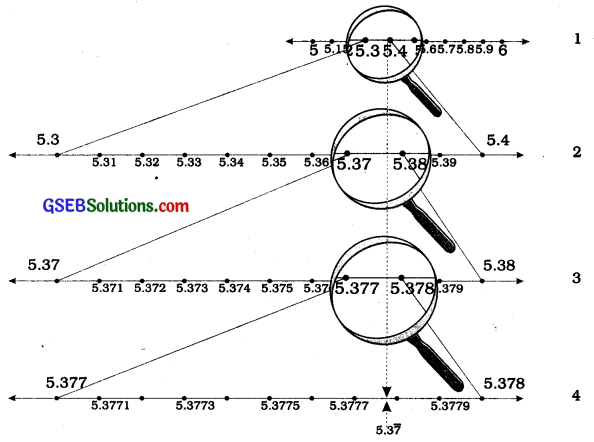
Remark: We can proceed endlessly in this manner, successively viewing through a magnifying glass and simultaneously imagining the decrease In the length of the portion of the number line in which 5.3v Is located. The size of the portion of the line we specify depends on the degree of accuracy we would like for the visualisation of the position of the number on the number line.

Operations on real numbers:
The commutative law, the associative law and the distributive law for addition and multiplication hold good for rational numbers as well as for irrational numbers.

→ Q, the collection of rational numbers, is closed for addition, subtraction, multiplication and division (divisor being non-zero). This means that the sum, difference, product and quotient of any two rational numbers is also a rational number.

→ Irrational numbers do not possess the property of closure. The sum, difference, product and quotient of two irrational numbers may or may not be an irrational number.

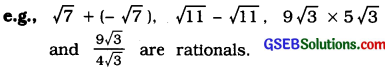
For two non-zero numbers-one of them being a rational and the other being an irrational-, their sum, difference, product and quotient are all irrational numbers.
Let a > 0 be a real number. Then, \(\sqrt{a}\) = b means b = a and b > 0.

→ If a is a positive real number and n is a positive integer, then there is one and Only one positive real number b such that bⁿ = a. This number b is called the positive nth root of a and is expressed as b = \(\sqrt[n]{a}\). Also, 0ⁿ = 0 and hence \(\sqrt[n]{0}\) = 0.

→ Let a, b, c and d be positive real numbers. Then,

→ Representation of \(\sqrt{a}\) on the number line for positive real number a: Earlier we have studied how to represent \(\sqrt{a}\) , for natural number a on the number line with the help of Pythagoras’ theorem.

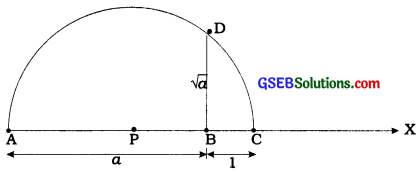
→ Now, we show how to represent \(\sqrt{a}\), a being any positive real number on the number line.
Steps of construction :

• Draw ray AX.
• Mark B on ray AX such that AB = a units.
• Mark C on ray BX such that BC = 1 unit.
• Let P be the midpoint of seg AC.
• Draw a semicircle with centre P and radius AE
• Draw perpendicular to seg AC at B inter-secting the semicircle at D.
• BD = \(\sqrt{a}\)

→ Now, taking line AX as the number line, B corresponding to 0 and BC = 1 unit, \(\sqrt{a}\) can be represented on the number line by drawing an arc with centre B and radius BD.
Note: This construction shows that for every positive real number a, \(\sqrt{a}\) exists.

→ Rationalization: If an irrational number is multiplied by some suitable irrational number which can make the product a rational number, then such a process is known as rationalization.

→ The suitable multiplier irrational number is called a rationalizing factor of the given irrational number, e.g., 5 \(\sqrt{3}\) when multiplied by \(\sqrt{2}\) gives the product 15. Thus, \(\sqrt{2}\) is a rationalizing factor of 5 \(\sqrt{2}\) . Similarly, (\(\sqrt{a}\) – \(\sqrt{b}\)) is a rationalizing factor of (\(\sqrt{a}\) + \(\sqrt{b}\)) ior positive real numbers a and b.

Rationalizing factor is not unique:
It is not easy to represent \(\frac{1}{\sqrt{5}}\) on the number line. But, if we rationalize its denominator \(\frac{1}{\sqrt{5}}=\frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{\sqrt{5}}{5}\) now 11 is easy to represent \(\frac{\sqrt{5}}{5}\) on the number line.

→ Note that the symbol \(\sqrt{}\) used in \(\sqrt{2}, \sqrt[3]{8}, \sqrt[n]{a}\) etc. is called the radical sign.

Example 1:
Check whether 7\(\sqrt{5}\), \(\frac{7}{\sqrt{5}}\) , \(\sqrt{2}\) + 21, ,π-2 are irrational numbers or not.
Answer:
√5 =2.236…, √2 = 1.4142… ,z=3.1415…

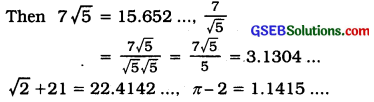
All these are non-terminating non-recurring decimals. So, all these are irrational numbers.

Example 2:
Add 2√2 + 5√3 and √2 – 3√3
Answer:

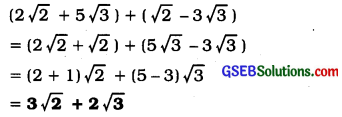
Example 3:
Multiply 6√5 by 2√5
Answer:
6√5 × 2√5 = 6 × 2 × √5 × √5 = 12 × 5 = 60

Example 4:
Divide 8√15 by 2√3.
Answer:

Example 5:
Simplify the following expressions:
(i)(5 + √7)(2 + √5)
Answer:
(5 + √7)(2 + √5) = 10 + 5 √5 + 2√7 + √35

(ii)(5 + √5)(5 – √5)
Answer:
(5 + √5)(5 – √5) = 5² – (√5)²
= 25 – 5 = 20

(iii) (√3 +√7)2
Answer:
(√3 +√7)² = (√3)² + 2√3√7 + (√7)²
= 3 + 2√21 + 7 = 10 + 2√21

(iv) (√11 — √7) (√11 + √7)
Answer:
(√11 — √7) (√11 + √7) = (√11)² – (√7)²
= 11 – 7 = 4

Example 6:
Rationalise the denominator of \(\frac{1}{\sqrt{2}}\).
Answer:
We want to write \(\frac{1}{\sqrt{2}}\) as an equivalent expression in which the denominator is a rational number. We know that √2. √2 is rational. We also know that multiplying \({\sqrt{2}{\sqrt{2}}\) by \(\frac{1}{\sqrt{2}}\) will give an equivalent expression, since \({\sqrt{2}{\sqrt{2}}\) = 1. So. we put these two facts together to get
\(\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}\)

In this form, It Is easy to locate \(\frac{1}{\sqrt{2}}\) on the number line. It is half way between 0 and √2

Example 7:
Rationalise the denominator of \(\frac{1}{2+\sqrt{3}}\)
Answer:

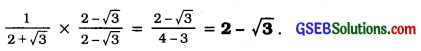
Example 8:
Rationalise the denominator of \(\frac{5}{\sqrt{3}-\sqrt{5}}\)
Answer:

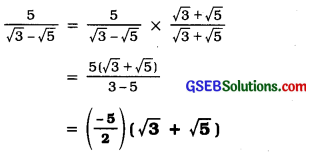
Example 9:
Rationalise the denominator of \(\frac{1}{7+3 \sqrt{2}}\)
Answer:

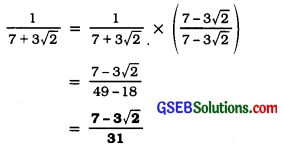
→ Laws of exponents for real numbers: For positive real numbers a and b and rational numbers p and q, we have

• a^p.a^q = a^p+q
• \(\frac{a^{p}}{a^{q}}\) = a^p-q
• (a^p)^q = a^pq
• (ab)^p = a^p . b^p
• \(\left(\frac{a}{b}\right)^{p}=\frac{a^{p}}{b^{p}}\)

We define a⁰ = 1 and a^-n = \(\frac{1}{a^{n}}\) for real number a, a ≠ 0 and n being a rational number.

Example 1:
Simplify:
(i) \(2^{\frac{2}{3}} \cdot 2^{\frac{1}{3}}\)
Answer:

(ii) \(\left(3 \frac{1}{5}\right)^{4}\)
Answer:
\(\left(3 \frac{1}{5}\right)^{4}\) = 3^4/5

(iii) \(\frac{7^{\frac{1}{5}}}{7^{\frac{1}{3}}}\)
Answer:

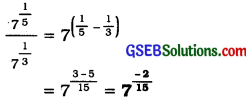
(iv) 13^1/5. 17^1/5
Answer:
(13 × 17)^1/5
= 221^1/5