GSEB Class 9 Maths Notes Chapter 2 Polynomials

This GSEB Class 9 Maths Notes Chapter 2 Polynomials covers all the important topics and concepts as mentioned in the chapter.

Polynomials Class 9 GSEB Notes

Variable:
A symbol which takes different numerical values is called a variable and it is denoted by x, y, z, etc.

Algebraic expression:

• Algebraic expression is a combination of a variable find constants which are joined by the signs like addition, subtraction, multiplication and division.
• In term 5x², 5 is the coefficient, x is the variable and 2 is the exponent.
• In algebraic expressions, the variables are usually denoted by x, y z, etc. and the coefficients are usually denoted by a, b, c, etc.

Polynomial:
An expression of the form a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2+ …. + a₁x + a₀; where a_n ≠ 0, a₀, a_1, a₂ an are constants and n is a whole number is called a polynomial in variable x. Polynomials are denoted by p(x), q(x), etc.

Degree of a polynomial:

• The highest power (index) of the variable in a polynomial is called the degree of the polynomial.
• Thus, p(x) = a_nxⁿ + a_n-1x^n-1 + … + a₁x + a₀; where a₀, a₁, a₂, ……….. an are constants,
  a_n ≠ 0, n is a whole number, is a polynomial of degree n.
• The degree of a non-zero constant polynomial is zero.
• The constant polynomial 0 is called the zero polynomial. The degree of the zero polynomial is not defined.

Linear polynomial:

• A polynomial of degree 1 is called a linear polynomial.
• The general form of a linear polynomial in one variable is ax + b; where a ≠ 0, a, b are constants.

Quadratic polynomial:

• A polynomial of degree 2 is called a quadratic polynomial.
• The general form of a quadratic polynomial in one variable is ax² + bx + c; where a ≠ 0, a, b, c are constants.

Cubic polynomial:

• A polynomial of degree 3 is called a cubic polynomial.
• The general form of a cubic polynomial in one variable is ax³ + bx² + cx + d; where a ≠ 0, a, b, c, d are constants.
• A polynomial having 1 term is called a monomial, having 2 terms is called a binomial and having 3 terms is called a trinomial.

Example 1:
Find the degree of each of the polynomials given below:
(i) x⁵ – x⁴ + 3
Answer:
The highest power of the variable is 5. So, the degree of the polynomial is 5.

(ii) 2 – y² – y³ + 2y⁸
Answer:
The highest power of the variable is 8. So, the degree of the poiynomlal is 8.

(iii) 2
Answer:
The only term here is 2, which can be written as 2x⁰. So, the exponent of x is 0. Therefore. the degree of the polynomial is 0.

Zeros of a polynomial:

• If for some real values of x, p (x) = 0, then those values of x are called zeros of the polynomial p (x).
• In other words, a zero of a polynomial p (x) Is a number c such that p (x) = 0.
  e.g., -3 Is the zero of the polynomial x + 3, while 2 and 3 are the zeros of the polynomial x² – 5x + 6.
• A non-zero constant polynomial like 7 = 7x has no zero and every real number x Is a zero of the zero polynomial.
• The zeros of the polynomial p (x) are also called the roots or solutions of the polynomial equation p(x) = 0.

Value of a polynomial:
ReplacIng x in p (x) by some real number α, we get the value of the polynomial p (x) at x = a. It Is denoted by p(a).

Example 1:
Find the value of each of the following polynomials at the indicated value of variables:
(i) p (x) = 5x² – 3x + 7 at x = 1.
Answer:
p(x) = 5x² – 3x + 7
The required value of the polynomial p (x) at x = 1 is given by
p(1) = 5(1)² – 3(1) + 7
= 5 – 3 + 7 = 9

(ii) q (y) = 3y³ – 4y + √11 at y = 2.
Answer:
q (y) = 3y³ – 4y +√11
The required value of the polynomial q (y) at y = 2 is given by
q (2) = 3 (2)³ – 4 (2) + √11
= 24 – 8 + √11
= 16 + √11

(iii) p (t) = 4t⁴ + 51³ – t² + 6 at t = a.
Answer:
p(t) = 4t⁴ + 5t³ – t² + 6
The required value of the polynomial p (t) at t = a is given by
p (a) = 4a⁴ + 5a³ – a² + 6

Example 2:
Check whether – 2 and 2 are zeroes of the polynomial x + 2.
Answer:
Let, p (x) = x + 2.
Then, p (2) = 2 + 2 = 4 and p(-2) = -2 + 2 = 0
Therefore, -2 is a zero of the polynomial x + 2, but 2 is not.

Example 3:
Find a zero of the polynomial p (x) = 2x + 1.
Finding a zero of polynomial p (x) is the
same as solving the equation p (x) = 0.
Now, 2x + 1 = 0 gives us x = – \(\frac{1}{2}\)
So, –\(\frac{1}{2}\) is a zero of the polynomial 2x + 1.

Example 4:
Verify whether 2 and 0 are zeroes of the polynomial x – 2x.
Answer:
Let, p (x) = x² – 2x
Then, p (2) = 2² – 2 (2) = 4 – 4 = 0
and p (0) = 0 – 0 = 0
Hence, 2 and 0 are both zeroes of the polynomial x² – 2x.

Division of a monomial by a monomial:
To divide a monomial by another monomial, the laws of Indices are used.

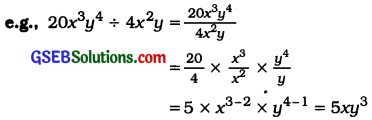
Quotient: 5xy³

Laws of Indices:
If m and n are positive integers and a ≠ 0, then

• a^m × aⁿ = a^m+n
• a^m + aⁿ = a^m-n (m > n)
• am ÷ aⁿ = \(\frac{1}{a^{n-m}}\) (m < n)
• a^m ÷ aⁿ = 1 (m = n)

We shall divide a monomial as below:

• We will write the dividend monomial In the numerator and the divisor monomial In the denominator.
• We will reduce the coefficients by factorizatlon and will use the laws of indices for the variables.

Division of a polynomial by a monomial:
There are three methods to divide a polynomial by a monomial:

• By the method of factorizatlon
• By dividing each term of the dividend polynomial by the divisor monomial
• By the method of long division

Division of a polynomial by a polynomial:
1. For dividing a polynomial by a polynomial. the degree of the dividend p (x) should be greater than or equal to the degree of the divisor g (x).

2. Arrange both the polynomials In descending order of the powers of some variable which Is common In both.

3. DivIde the first term of the dividend by the first term of the divisor to get the first term of the quotient.

4. Multiply all the terms of the divisor by the first term of the quotient and subtract It from the dividend to get a new dividend.

5. Proceed in this manner till the degree of the new dividend Is less than that of the divisor. The answer will be expressed In terms of quotient and remainder.

6. The relation between the dividend, the divisor, the quotient and the remainder is given by
Dividend = divisor × quotient + remainder.
p(x) = g(x).q(x) + r(x)
where, p (x) = the dividend
g(x) = the divisor
q (x) = the quotient
r(x) = the remainder

Remainder theorem:
Let p (x) be any polynomial of degree greater than or equal to one and let a be any real number. if p (x) is divided by the linear polynomial x – a, then the remainder Is p (a).

Proof: Let p (x) be any polynomial with degree greater than or equal to 1. Suppose that when p (x) Is divided by x – a, the quotient Is q (x) and the remainder Is r (x),
i.e.. p(x) = (x – a) q(x) + r(x).

Since the degree of x – a is 1 and the degree of r (x) Is less than the degree of x – a, the degree of r (x) = 0. This means that r (x) Is a constant, say r.
So, for every value of x, r (x) = r.
Therefore, p (x) = (x – a) q (x) + r.

In particular, if x = a, this equation gives us
p(a) = (a – a)q(a) + r
= r
which proves the theorem.

Example 1:
Divide p (x) by g (x), where p (x) = x + 3x – 1 and g (x) = 1 + x.
‘We carry out the process of division by means of the following steps:
Step 1:
We write the dividend x + 3x² – 1 and the divisor 1 + x in the standard form, i.e., after arranging the terms in the descending order of their degrees. So, the dividend is 3x² + x – 1 and divisor is x + 1.

Step 2:
We divide the first term of the dividend by the first term of the divisor, i.e., we divide 3x² by x, and get 3x. This gives us the first term of the quotient.
\(\frac{3 x^{2}}{x}\) = 3x = First term of quotient

Step 3:
We multiply the divisor by the first term of the quotient, and subtract this product from the dividend, i.e., we multiply x + 1 by 3x and subtract the product 3x² + 3x from the dividend 3x² + x – 1. This gives us the remainder as – 2x – 1.

Step 4:
We treat the remainder – 2x – 1 as the new dividend. The divisor remains the same. We repeat step 2 to get the next term of the quotient, i.e., we divide the first term -2x of the (new) dividend by the first term x of the divisor and obtain -2. Thus, -2 is the second term in the quotient.
\(\frac{-2 x}{x}\) = – 2 = Second term of quotient New quotient = 3x – 2

Step 5:
We multiply the divisor by the second term of the quotient and subtract the product from the dividend. That is, we multiply x + 1 by -2 and subtract the product – 2x – 2 from the dividend -2x – 1. This gives us 1 as the remainder.

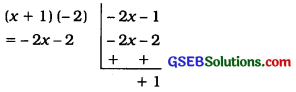
This process continues till the remainder is 0 or the degree of the new dividend is less than the degree of the divisor. At this stage, this new dividend becomes the remainder and the sum of the quotients gives us the whole quotient.

Step 6:
Thus, the quotient in full is 3x – 2 and the remainder is 1.
Let us look at what we have done in the process above as a whole:

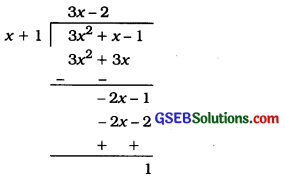
Notice that 3x² + x – 1 = (x + 1)(3x – 2) + 1
i. e., Dividend = (Divisor × Quotient) + Remainder
In general, if p (x) and g (x) are two polynomials such that degree of p (x) ≥ degree of g (x) and g (x) ≠ 0, then we can find polynomials q (x) and r (x) such that:
p (x) = g (x) q (x) + r (x); where, r (x) = 0 or degree of r (x) < degree of g (x). Here we say that p (x) divided by g (x), gives q (x) as quotient and r (x) as remainder.

Example 2:
Divide the polynomial 3x⁴ – 4x³ – 3x – 1 by x- 1.
Answer:
By long division, we have:

∴ 3x⁴ – 4x³ – 3x – 1 = (x – 1) (3x³ – x² – x – 4) + (-5)
Here, the remainder is -5. Now, the zero of x-1 is 1. So, putting x = 1 in p (x), we see that
p(1) = 3 (1)⁴ – 4 (1)³ – 3 (1) – 1 = 3 – 4 – 3 – 1
= – 5, which is the remainder.

Example 3:
Find the remainder obtained on dividing p (x) = x³ + 1 by x + 1.
Answer:
By long division,

So, we find that the remainder is 0.
Here, p (x) = x³ + 1, and the root of x + 1 = 0 is x = – 1. We see that
p (-1) = (-1)³ + 1
= – 1 + 1
= 0
which is equal to the remainder obtained by actual division.

Example 4:
Find the remainder when x⁴ + x³ – 2x² + x + 1 is divided by x – 1.
Answer:
Here, p (x) = x⁴ + x³ – 2x² + x + 1 and the zero of x – 1 is 1.
So, p(1) = (1)⁴ + (1)³ – 2(1)² + 1 + 1
= 2

So, by the remainder theore m, 2 is the remainder when x⁴ + x³ – 2x² + x + 1 is divided by x- 1.

Example 5:
Check whether the polynomial q (t) = 4t³ + 4t² -1 – 1 is a multiple of 2t + 1.
Answer:
As you know, q (t) will be a multiple of 2t + 1 only, if 2t + 1 divides q (t) leaving remainder zero. Now, taking 2t + 1 = 0, we have t = – \(\frac{1}{2}\)
Also,

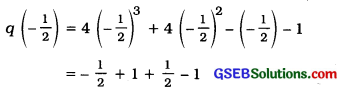
= 0
So, the remainder obtained on dividing q (t) by 2t + 1 is 0.
So, 2t + 1 is a factor of the given polynomial q (t), that is q (t) is a multiple of 2t + 1.

Factor theorem:
If p (x) is a polynomial of degree n ≥ 1 and a is a real number, then

• x – a Is a factor of p (x) if p (a) = O, and
• p(a) = 0 If (x – a) Is a factor of p (x).

In short, x – a is factor of p (x) if and only if p(a) = 0.

Proof: By the remainder theorem.
p(x) = (x – a)q(x) + p(a).

• If p(a)= 0. then p(x) = (x – a)q(x), which shows that x – a is a factor of p (x).
• Since x – a is a factor of p(x). p(x) = (x – a) g (x) for some polynomial g (x). In this case, p (a) = (a – a) g (a) = 0.
• (x – 1) is a factor of p (x) if and only if the sum of all the coefficients of p (x) Is zero.
• (x + 1) Is a factor of p (x) If and only If the sum of the coefficients of odd powers of x In p (x) Is equal to the sum of the coefficients of even powers of x In p (x).

Factorizatlon of polynomiale ax² + bx + c, a ≠ 0 and ax³ + bx² + cx + d, a ≠ 0:
A quadratic polynomial ax² + bx + e can be factorized Into two linear polynomials (px + 1)(qx + m). Then.
ax² + bx + c =(px + 1)(qx + m)
= pqx² + (pm + lq)x + lm
This shows that a = pq, b = pm + lq and c = lm.
Here, b is the sum of two numbers pm and lq whose product Is
(pm). (lq) = (pq) . (lm) = a . c.
Thus, to factorize ax² + bx + c, we have to find two factors of product ac such that their sum is equal to b.

This process is known as splitting the middle term,
To factorize polynomials of degree greater than 2, If a factor (x – a) Is obtained with the help of factor theorem, the other factors can be obtained by splitting all the terms except the first and the Last term In such a manner that the known factor (x – a) and other factors are received.
e.g., x³ + 10x² + 31x + 30
Let p(x) = x³ + 10x + 31x + 30
∴ p (-2) = (-2) + 10 (- 2)² + 31 (-2) + 30
= -8 + 40 – 62 + 30
= 0
Hence. x + 2 is a factor of p (x).
x³ + 10x² + 31x + 30
= x³ + 2x² + 8x² + 16x + 15x + 30
= x²(x + 2) + 8x(x + 2)+ 15(x + 2)
= (x + 2)(x² + 8x + 15)
= (x + 2)(x² + 5x + 3x + 15)
= (x + 2) {x(x + 5)+ 3(x + 5)}
= (x + 2)(x + 5)(x + 3)
If splitting of terms Is not convenient, one can also use long division for dividing p (x) by known factor (x – a).

Example 1:
Examine whether x + 2 is a factor of x³ + 3x² + 5x + 6 and of 2x + 4.
Answer:
The zero of x + 2 is – 2.
Let, p (x) = x³ + 3x² + 5x + 6 and s (x) = 2x + 4
Then, p (-2) = (-2)³ + 3 (-2)² + 5 (-2) + 6
= – 8 + 12 – 10 + 6
= 0
So, by the factor theorem, x + 2 is a factor of x³ + 3x² + 5x + 6.
Again, s (- 2) = 2 (- 2) + 4 = 0
So, x + 2 is a factor of 2x + 4.

Example 2:
Find the value of k, if x-1 is a factor of 4x³ + 3x² – 4x + k.
Answer:
As x – 1 is a factor of p (x) = 4x³ + 3x² – 4x + k,
p(1) = 0
Now, p(1) = 4(1 )³ + 3(1 )² – 4(1) + k
So, 4 + 3 – 4 + k = 0
i.e., k = – 3

Example 3:
Factorise 6x² + 17x + 5 by splitting the middle term, and by using the factor theorem.
Answer:
Method 1: (By splitting the middle term):
If we can find two numbers p and q such that p + q = 17 and pq = 6x⁵ = 30, then we can get the factors.
Out of the pairs of factors p and q of 30, 2 and 15 will give us p + q = 17.
So, 6x² + 17x + 5 = 6x² + (2 + 15) x + 5
= 6x² + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1)
= (3x + 1) (2x + 5)

Method 2: (Using the factor theorem)
6x² + 17x + 5 = 6\(\left(x^{2}+\frac{17}{6} x+\frac{5}{6}\right)\) = 6p (x), say.
If a and b are the zeroes of p (x), then 6x² + 17x + 5 = 6 (x – a) (x – b). So, ab = \(\frac{5}{6}\).

Let us look at some possibilities for a and b. They could be \(\pm \frac{1}{2}, \pm \frac{1}{3}, \pm \frac{5}{3}, \pm \frac{5}{2}, \pm 1\)

Similarly, by trial, you can find that (x + \(\frac{5}{2}\)) is a factor of p (x).
Therefore, 6x² + 17x + 5 = 6(x + \(\frac{1}{3}\))(x + \(\frac{5}{2}\))
= 6\(\left(\frac{3 x+1}{3}\right)\left(\frac{2 x+5}{2}\right)\)
= (3x + 1) (2x + 5)

Example 4:
Factorise y² – 5y + 6 by using the factor theorm.
Answer:
Let, p (y) = y² – 5y + 6. Now, if p (y) = (y – a) (y – b), we know that the constant term will be ab. So, ab = 6. So, to look for the factors of p (y), we look at the factors of 6.
The factors of 6 are ±1, ±2, ±3 and ±6.
Now, p (2) = 2² – (5 × 2) + 6 = 0
So, y – 2 is a factor of p (y).
Also, p (3) = 3² – (5 × 3) + 6 = 0
So, y – 3 is also a factor of y² – 5y + 6.
Therefore, y² – 5y + 6 = (y – 2) (y – 3)

Example 5:
Factorise : x³ – 23x² + 142x – 120.
Answer:
Let. p (x) = x³ – 23x² + 142x- 120 We shall now look for all the factors of -120. Some of these are ±1, ±2, ±3, ±4, ±5, ±6, ±8, ±10. ±12, ±15. ±20. ±24, ±30, ±60.
By trial, we find that p(1) = 0. So, x-1 is a factor of p (x).
Now, x³ – 23x²+ 142x – 20
= x³ – x² – 22x² + 22x + 120x- 120
= x²(x – 1) -22x (x – 1) + 120 (x – 1)
= (x – 1)(x² – 22x + 120)
[Taking (x – 1) common]
We could have also got this by dividing p (x) by x – 1.
Now, x² – 22x – 120 can be factorised either by splitting the middle term or by using the factor theorem. By splitting the middle term, we have:
x² – 22x + 120 = x² – 12x- 10x + 120
= x(x- 12)- 10 (x- 12)
= (x – 12) (x – 10)
So,
x³ – 23x² + 142x – 120 = (x – 1) (x – 10) (x – 12)

Algebraic identities:

• (x + a)(x + b) = x² + (a + b) x + ab
• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• (a + b) (a – b) = a² – b²
• (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
• (a + b)³ = a³ + 3a²b + 3ab² + b³ = a³ + b³ + 3ab (a + b)
• (a – b)³ = a³ – 3a²b + 3ab² – b³ = a³ – b³ – 3ab (a – b)
• a³ + b³ + c³ – 3abc = (a + b + c) (a² + b² + c² – ab – bc – ca)

All the above identities, read as they are, give us the expansion formulae.
But, if the sides L.H.S. and R.H.S. are interchanged, they give us factorization of the polynomials.

This shows that the expansion and the factorization are reverse processes.
From identity (6) and (7), we get
a³ + b³ = (a + b)³ – 3ab (a + b)
and a³ – b³ = (a – b)³ + 3ab (a – b).

Two more identities:

• a³ + b³ = (a + b) (a² – ab + b²)
• a³ – b³ = (a – b) (a² + ab + b²)
• An important result: Ff-om the identity a³ + b³ + c³ – 3 abc = (a + b + c) (a² + b² + c² – ab – be – ca), we get an important result that if a + b + c = 0, then a³ + b³ + c³ = 3abc.
• As all the above given results are identities, the letters a, b, c, x, etc. can be replaced by any other letters or numericals.

Example 1:
Find the following products using appropriate identities:
(i)(x + 3)(x + 3)
Answer:
ReplacIng a by x and b by 3 In
(a + b)² = a² + 2ab + b². we get
(x + 3)(x + 3) = (x + 3)²
= x² + 2 (x)(3) + (3)²
= x² + 6x + 9

(ii)(x – 3)(x + 5)
Answer:
Replacing a by -3 and b by 5 In
(x + a)(x + b) = x² + (a + b)x + ab, we get
(x – 3)(x + 5) = x² + (-3 + 5)x + (-3)(5)
= x² + 2x – 15

Example 2:
Evaluate 105 × 106 wIthout multiplying directly.
Answer:
105 × 106 = (100 + 5) × (100 + 6)
=(100)² + (5 + 6)(100) + (5 × 6)
= 10000 + 1100 + 30
= 11130

Example 3:
Factorise:
(i) 49a² + 70ab + 25b²
Answer:
Here, 49a² = (7a)²+ 25b² = (5b)².
70ab = 2 (7a) (5b)
Now a² + 2ab + b² = (a + b)²
= 49a² + 70ab + 25b²
= (7a)² + 2(7a) (5b) + (5b)²
= (7a + 5b)² = (7a + 5b) (7a + 5b)

(ii) \(\frac{25}{4}\)x² – \(\frac{y^{2}}{9}\)
Answer:

Example 4:
Write (3a + 4b + 5c)² in expanded form.
Answer:
In the identity.
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca,
we replace a by 3a, b by 4b and e by 5e.
Therefore,
(3a + 4b + 5c)² = (3a)² + (4b)² + (5c)² + 2 (3a) (4b) + 2(4b)(5c) + 2(5c)(3a)
= 9a² + 16b² + 25c² + 24ab + 40bc + 30ac

Example 5:
Expand (4a – 2b – 3c)².
Answer:
(4a – 2b – 3c)² = [4a + (-2b) + (-3c)]²
= (4a)² + (- 2b)² + (- 3c)² + 2 (4a) (- 2b) + 2(-2b)(-3c) + 2(-3c)(4a)
= 16a² + 4b² + 9c² – l6ab + 12bc – 24ac

Example 6:
Factorise 4x² + y² + z² – 4xy – 2yz + 4xz.
Answer:
4x² + y² + z² – 4xy – 2yz + 4xz
= 2x² + (-y)² + (z)² + 2 (2x)(-y) + 2(-y)(z) + 2(2x)(z)
= [2x + (-y) + z]²
= (2x – y + z)² = (2x – y + z)(2x – y + z)

Example 7:
Write the following cubes In the expanded form:
(I) (3a + 4b)³
Answer:
We know. (a + b)³ = a³ + b³ + 3ab(a + b)
∴ (3a + 4b)³
= (3a)³ + (4b)³ + 3 (3a)(4b) (3a + 4b)
= 27a³ + 64b³ + 108a²b + 144ab²

(II)(5p – 3q)³
Answer:
We know, (a – b)³ =a³ – b³ -3ab(a-b)
∴ (5p – 3q)³
= (5p)³ – (3q)³ – 3 (5p) (3q) (5p – 3q)
= 125p³ – 27q³ – 225p²q + 135pq²

Example 8:
Evaluate each of the following using suitable identities:
(i) (104)
Answer:
(104) = (100 + 4)
(100) + (4) + 3(100)(4)(100 + 4)
= 1000000 + 64 + 124800
= 1124864

(ii) (999)³
Answer:
(999)³ = (1000 – 1)
= (1000) – (1) – 3 (1000) (1)(1000 – 1)
= 1000000000 – 1 – 2997000
= 997002999

Example 9:
Factorise 8x³ + 27y³ + 36x²y + 54xy²
Answer:
The given expression can be written as
(2x)³ + (3y)³ + 3 (4x²)(3y) + 3 (2x) (9y²)
= (2x)³ + (3y)³ + 3 (2x)² (3y) + 3 (2x) (3y)²
= (2x + 3y)³
= (2x + 3y) (2x + 3y) (2x + 3y)

Example 10:
Factorise 8x³ + y³ + 27z³ – 18xyz
Answer:
8x³ + y³ + 27z³ – 18xyz
= (2x)³ + y³ + (3z)³ – 3(2x) (y) (3z)
= (2x + y + 3z) [(2x)² + y² + (3z)² – (2x) (y) – (y) (3z) – (2x) (3z)]
= (2x + y + 3z) (4x² + y² + 9z² – 2xy – 3yz – 6xz)