Gujarat Board GSEB Textbook Solutions Class 11 Chemistry Chapter 2 Structure of Atom Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Chemistry Chapter 2 Structure of Atom
GSEB Class 11 Chemistry Structure of Atom Text Book Questions and Answers
Question 1.
- Calculate the number of electrons that will together weigh one gram.
- Calculate the mass and charge of one mole of electrons.
Solution:
(1) 9.1 × 10-28 g is the weight of 1 electron
∴ 1 g of the weight of \(\frac{1}{9.1 \times 10^{-28}}\) electrons
= 1.099 × 1027 electrons
∴ No. of electrons weighing 1 g = 1.099 × 1027 electrons.
(2) Mass of one electron = 9.1 × 10-31 kg .
∴ Mass of 1 mole (6.023 × 1023) electrons
= 9.1 × 10-31 × 6.023 × 1023 kg
= 5.48 × 10-7 kg
Charge on one electron = 1.602 × 10-19 coulomb
∴ Charge on 1 mole (6.023 × 1023) electrons
= 1.602 × 10-19 × 6.023 x 1023 coulomb
= 9.65 × 104 C
![]()
Question 2.
(1) Calculate the total number of electrons present in one mole of methane.
(2) Find
(a) the total number and
(b) the total mass of neutrons in 7 mg of 14C. (Assume that mass of a neutron = 1.675 × 10-27 kg)
(3) Find
(a) the total number and
(b) the total mass of protons in 34 mg of NH3 at STP. Will the answer change if the temperature and pressure are changed?
Solution:
(1) 1 mole of methane (CH4) contains 1 mole of C atoms and 4 moles of H atoms.
Each mole of C atoms contains 6 moles of electrons and each mole of H atoms contains 1 mole of electrons
∴ Total no. of electrons present in one mole of CH4
= (6 × 6.023 × 1023 + 4 × 6.023) electrons
= 3.614 × 1024 + 2.409 × 1024 electrons
= 6.022 × 1024 electrons
(2) (a) Mass of a neutron = 1.675 × 10-27 kg
14.0 g of 14C contains 1 mole of atoms of C-14 [each atom of C-14 contains 8 neutrons]
∴ 14.0 g of 14C contains 8 × 6.023 × 1023 neutrons
7 mg (= 7 × 10-3g) of C contains = ![]()
= 2.409 × 1021 neutrons
(b) Total mass of neutrons as in (a) above 7 mg of 14C contains 2.409 × 1021 neutrons
The mass of 1 neutron = 1.675 × 10-27 kg [Given]
∴Mass of 2.409 × 1021 neutrons (contained in 7 mg of 14C)
= 2.409 × 1021 × 1.675 × 10-27 kg
= 4.0347 × 10-6 kg
(3) (a) The total number of protons in 34 mg of NH3 17.0 g of NH3 contains 1 mole of N atoms and 3 mols of H atoms.
i.e., 17.0 g of NH3 contains 7 mols of protons of N and 3 mols of protons of H
= 10 moles of protons = 10 × 6.022 × 1023 protons
34 × 10-3 g of NH3 contains = ![]()
1.2044 × 1022 protons.
(b) No. of protons in 34 × 10-3 g of NH3 = 1.2044 × 1022 protons
Mass of 1 proton = 1.675 × 10-27
Mass of 1.2044 × 1022 protons = 1.675 × 10-27 × 1.2044 × 1022 kg
= 2.015 × 10-5 kg
There is no effect of temperature and pressure.
![]()
Question 3.
How many neutrons and protons are there in the following nuclei?
![]()
Solution:
No. of neutrons present in \({ }_{6}^{13} \mathrm{C}\) = Mass no. – Atomic no. = 13 – 6 = 7
No. of protons present in \({ }_{6}^{13} \mathrm{C}\) = Atomic no. = 6
No. of neutrons present in \({ }_{8}^{16} \mathrm{O}\) = 16 – 8 = 8
No. of protons = 8
No. of neutrons in \({ }_{12}^{24} \mathrm{Mg}\) = 24 – 12 = 12
∴ No. of protons = 12
No. of neutrons present in \({ }_{26}^{56} \mathrm{Fe}\) = 56 – 26 = 30
No. of protons = 26
No. of neutrons present in \({ }_{38}^{88} \mathrm{Sr}\) = 88 – 38 = 50
No. of protons = 38.
Question 4.
Write the complete symbol for the atom with the given atomic number (Z) and atomic mass (A)
- Z = 17, A = 35
- Z = 92, A = 233
- Z = 4, A = 9
Solution:
(1) Z = 17, A = 35
Since the no. of protons = 17 = no. of electrons
∴The atom in chlorine = Cl : \({ }_{17}^{35} \mathrm{Cl}\)
(2) Z = 92, A = 233
No. of protons = 92
∴ The atom is Uranium = U : \({ }_{92}^{233} \mathrm{U}\)
(3) Z = 4, A = 9. .
No. of protons = 4
∴ The atom is Beryllium = Be: \({ }_{4}^{9} \mathrm{Be}\)
Question 5.
Yellow light emitted from a sodium lamp has a wavelength (λ) of 580 nm. Calculate the frequency (ν) and wavenumber \((\bar{v})\) of the yellow light.
Solution:
Wavelength (λ) of yellow light = 580 nm = 580 × 10-9 m
Frequency of yellow light (v) ![]()
Wavenumber \((\bar{v})\) of yellow light ![]()
![]()
Question 6.
Find the energy of each of the photons which
- correspond to light of frequency 3 × 1015 Hz
- have a wavelength of 0.50Å
Solution:
(1) To calculate the energy of a photon whose frequency (v) = 3 × 1015 Hz = 3 × 1015 cps (1 Hz = 1 cycle sec-1)
E = hv
Where h = Planck’s constant = 6.6 × 10-34Js
E = 6.6 × 10-34 × 3 × 1015
= 1.98 × 10-18J
(2) E = hv = \(\frac { hc }{ λ }\) [∵ v = \(\frac { c }{ λ }\)]
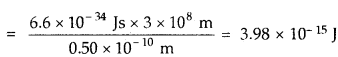
Question 7.
Calculate the wavelength, frequency, and wavenumber of a light wave whose period is 2.0 × 10-10 s.
Solution:
(T) Period of the wave = 2.0 × 10-10 s
∴ Frequency, v = \(\frac { 1 }{ T }\) = ![]() = 5 × 109 s-1
= 5 × 109 s-1
Now, c = v × λ
3 × 108 = 5 × 109 × λ
λ =  = 6.0 × 10-2 m
= 6.0 × 10-2 m
Wave number \(\bar{v}\) = \(\frac { 1 }{ λ }\) = ![]() = 16.66 m-1
= 16.66 m-1
![]()
Question 8.
What is the number of photons of light with a wavelength of 4000 pm that provides 1 J of energy?
Solution:
Energy of photon Ephoton = hv =\(\frac { hv }{ λ }\)
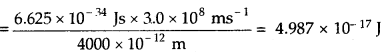
∴ 1 Joule of energy![]() photons.
photons.
Question 9.
A photon of wavelength 4 × 10-7 m strikes on the metal surface, the work function of the metal is 2.13 eV. Calculate
- the energy of the photon (eV),
- the kinetic energy of the emission, and
- the velocity of the photoelectron (1 eV = 1.6020 × 10-19J).
Solution:
Energy (E) = \(\frac { hc }{ λ }\); where h = 6.6 × 10-34 Js; c = 3 × 108 ms-1
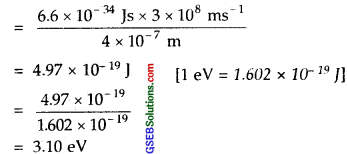
(1) Energy of the photon in eV = 3.10
(2) Kinetic energy of the emission of photoelectron (K.E.)
= hv – W0; where W0 = work function.
= 3.10 eV – 2.13 eV = 0.97 eV
(3) Velocity of the photoelectron
Since K.E. = \(\frac { 1 }{ 2 }\) mν2 or ν2= \(\frac{2 \times \mathrm{K.E}}{m}\)
or 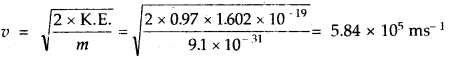
Question 10.
Electromagnetic radiation of wavelength 242 nm is just sufficient to ionize the sodium atom. Calculate the ionization energy of sodium in kJ mol-1
Solution:
Wave length, λ = 242 nm = 242 × 10-9m
Energy per photon (E) 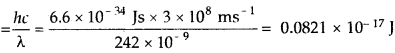
Since this energy is sufficient to cause ionization of one atom of Na
∴ Ionization energy for 1 mole 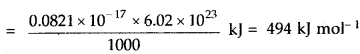
![]()
Question 11.
A 25-watt bulb emits monochromatic yellow light of a wavelength of 0.57μ m. Calculate the rate of emission of quanta per second.
Solution:
The energy of one photon (E) = hv = \(\frac { hc }{ λ }\)
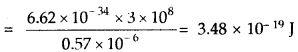
Now, 25 watt = 25 Js-1
∴ rate of emission of quanta per second
Question 12.
Electrons are emitted with zero velocity from the metal surface When it is exposed to radiation of wavelength 6800 A. Calculate threshold frequency,(v0) and work function (w0) of the metal.
Solution:
K.E. = hv – hv0
Since electrons are emitted with zero velocity
∴ K.E. = 0
∴ h = (v – v0) = 0
v0 = 0
v0 = \(\frac { c }{ λ }\) = \(\frac{3 \times 10^{8}}{6800 \times 10^{-10}}\) = 4.41 × 1014 s-1
∴ Threshold frequency (v0) = 4.41 × 1014 s-1
work function,W0 = hv0 = 6.6 × 10-34 × 4.41 × 1014 J
= 2.91 × 10-19 J
Question 13.
What is the wavelength of light emitted when the electron in a hydrogen atom undergoes a transition from an energy level with n = 4 to an energy level with n = 2?
Solution:
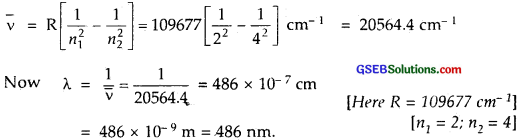
Question 14.
How much energy is required to ionize an H atom if the electron occupies n = 5 orbits? Compare your answer with the ionization enthalpy of the H atom [energy required to remove the electron from n = 1 orbit]
Solution:
The energy required to ionize the H atom when the electron is in the 5th orbit can be thus calculated: n1 = 5; n2 = ∝

∴ The energy required to ionize this H atom = + 8.72 × 10-20 J
Ionization energy-(i.e., the energy required to remove the electron from n = 1 orbit) of H atom
Here n1 = 1, n2 = ∞

Thus, far higher energy (25 times) required to remove an electron from 1st orbit.
![]()
Question 15.
What is the maximum number of emission lines when the excited electron of an H atom in n = 6 drops to the ground state?
Solution:
Maximum number of emission lines ![]()
Question 16.
- The energy associated with the first orbit in a hydrogen atom is – 2.18 × 1018 J atom-1. What is the energy associated with the fifth orbit?
- Calculate the radius of Bohr’s fifth orbit for H.
Solution:
(1) The energy of the nth orbit in H atom = – 2.18 × 1018/n2J atom-1
For the first orbit, E1 ![]()
For the fifth orbit, E5 ![]()
(2) Calculation of the radius of Bohr’s fifth orbit for the Hydrogen atom
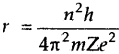
For Hydrogen n = 1; Z = 1; putting usual values of π, m, h, e radius (r0) = 0.529 Å This is known as Bohr’s radius.
For H-atom, the radius of any orbit (r0)
= n2 × r0 where n = number of the orbit.
= 52 × (0.529) Å = 1.3225 nm
Question 17.
Calculate the wavenumber of the longest wavelength transition in the Balmer series of atomic hydrogen.
Solution:
For Balmer series n1 = 2. Hence

Now \(\bar{v}=\frac{1}{\lambda}\)Hence λ will be longest when \(\bar{v}\) is shortest, which,in turn will be shortest if n2 is shortest i.e., when n2 = 3.
![]()
![]()
Question 18.
What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit, and what is the wavelength of the light emitted when the electron returns to the ground state? The ground-state electron energy is – 2.18 × 10-11 ergs.
Solution:
The ground-state electron is the energy of the electron in the first Bohr’s orbit
– 2.18 × 10-11 ergs [Given]
E1 = – 2.18 × 10-18J [1 J = 107ergs]
En = Energy in the nth orbit
\(\frac{-2.18 \times 10^{-18}}{n^{2}}\) where n = no. of the orbit
E5 = \(\frac{-2.18 \times 10^{-18}}{5^{2}}\) = 8.72 × 10-20J
Energy has to be absorbed to shift electrons from Bohr’s first orbit to the fifth orbit.
∴ △E = E1 – E2 = -2.18 × 10-18\(\left[\frac{1}{5^{2}}-\frac{1}{1^{2}}\right]\)
= 2.18 × 10-18\(\left[\frac{24}{25}\right]\) = 2.08 × 10-18J
= 2.18 × 10-11 ergs.
△E = \(\frac { hc }{ λ }\)
or ![]()
The wavelength of the light emitted = 956 Å
Question 19
The electron energy in a hydrogen atom is given by En = (- 2.18 × 10-18)/n2 J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Solution:
For n = 2
E2 = \(\frac{-2.18 \times 10^{-18}}{2^{2}}\) J = -5.45 × 10-19J
The energy required to remove this electron completely in the case of H atom = + 5.45 × 10-19 J
[∵ E∞ = 0; so △E = E∞ – E2 = 0 – 5.45 × 10-19 J = + 5.45 × 10-19 J]
Now, △E = hv = \(\frac { hc }{ λ }\)
∴ λ = \(\frac { hc }{ △E }\) = \(\frac{6.66 \times 3.0 \times 10^{8} \times 10^{-34}}{5.45 \times 10^{-19}}\)m
= 3.647 × 10-7 m = 3647 Å
Question 20.
Calculate the wave length of an electron moving with a velocity of 2.05 × 107 ms-1
Solution:
Mass of an electron = me = 9.1 × 10-31 kg
Now h = Planck’s constant = 6.625 × 10-34 Js,
ν = velocity = 2.05 × 107 ms-1, λ = ?
λ = \(\frac{h}{m \times v}\) = \(\frac{6.635 \times 10^{-34}}{9.1 \times 10^{-31} \times 2.05 \times 10^{7}}\)
= 0.355 × 10-10m = 3.55 × 10-11m
![]()
Question 21.
The mass of an electron is 9.1 × 10-31 kg. If it’s K.E. is. 3.0 × 10-25 J, calculate its wavelength.
Solution:
K.E. = \(\frac { 1 }{ 2 }\)mv2
The velocity of the electron

Now, λ = \(\frac{h}{m \times v}\) = \(\frac{6.625 \times 10^{-34}}{9.1 \times 10^{-31} \times 0.812 \times 10^{3}}\)
= 0.8965 × 10-6 m
wavelength = λ = 0.8965 × 10-6 = 8965 Å.
Question 22.
Which of the following are isoelectronic species i.e., those having the same number of electrons?
Na+, K+, Mg2+, Ca2+, S2-, Ar
Solution:
No. of electrons in Na+ = 10 [11-1]
No. of electrons in K+ = 18 [19-1]
No. of electrons in Mg2+ = 10 [12-2]
No. of electrons in Ca2+ = 18 [20 – 2]
No. of electrons in S2- = 18 [16 + 2]
No. of electrons in Ar = 18
∴ Na+, Mg2+ are isoelectronic (10e- each) .
∴ Ca2+, K+, S2-, Ar are isoelectronic (18e- each).
![]()
Question 23.
(1) Write the electronic configurations of the following ions :
- H–
- Na+
- O2-
- F–
(2) What is the atomic number of elements whose outermost electrons are represented by
- 3s1
- 2p3 and
- 3p5
(3) Which atoms are indicated by the following configurations?
- [He] 2s1
- [Ne] 3s2 3p3
- [Ar] 4s23d1
Solution:
(1)
- Electronic configuration of H– = 1 + 1 = 2 = 1s2
- Na+ = 11 – 1 = 10 = 1s2, 2s22p6
- O2- = 8 + 2 = 10 = 1s2, 2s22p6
- F– = 9 + 1 = 10 = 1s2, 2s22p6
(2)
- 3s1; It is sodium whose configurations is 1s2, 2s22p6, 3s1= Its Atomic number is 11.
- 2p3; It is nitrogen whose configuration is 1s2, 2s2, 2p3 Its Atomic number is 7
- 3p5; It is chlorine whose configuration is 1s2, 2s22p6, 3s2 3p5 Its Atomic number is 17
(3)
- [He] 2s1, i.e., 1s2, 2s1; It is Lithium whose Z = 3
- [Ne] 3s23p3, i.e., 1s2,2s2 2p6, 3s2 3p3; It is phosphorus (P) whose Z = 15
- [Ar] 4s23d1, i.e., 1s22s22p6,3s23p6, 4s23d1 is Scandium (Sc) whose Z = 21.
Question 24.
What is the lowest value of ft that allows g orbitals to exist?
Solution:
For n; the values of l are 0,1, ………… (n -1)
∴ For n = 5; the values of l are 0, 1, 2, 3, 4
For l = 4; g subshell can exist. Hence the lowest value of n = 5.
Question 25.
An electron is in one of the 3d orbitals. Give the possible values of n,l, and m1, for this electron.
Solution:
When n = 3
1 = 2 [Since it is in 3d subshell]
m1, = – 2, – 1, 0, + 1, + 2 [Any one of the values]
Question 26.
An atom of an element contains 29 electrons and 35 neutrons. Deduce
- the number of protons and
- the electronic configuration of the element.
Solution:
- No. of protons = No. of electrons = 29 (since the atom is electrically neutral)
- Atomic No. = 29
∴ Electronic configuration = 1s22s22p63s23p63d104s1
Question 27.
Give the number of electrons in the species \(\mathrm{H}_{2}^{+}\) , H2 and \(\mathrm{O}_{2}^{+}\)
Solution:
\(\mathrm{H}_{2}^{+}\) = 2 – 1 = 1
H2 = 2
\(\mathrm{O}_{2}^{+}\) = 16 – 1 = 15
![]()
Question 28.
- An atomic orbital has n = 3, What are the possible values of l and m1?
- List the quantum numbers (m1 and l) of electrons for 3d orbital.
- Which of the following orbitals are possible?
1p, 2s, 2p and 3f.
Solution:

- For 3d orbital; l = 2
The values of m1 are – 2, – 1, 0, +1, + 2 - Out of 1p, 2s, 2p, and 3f, only 2s and 2p are possible.
Question 29.
Using. s, p, d, f notations, describe the orbital with the following quantum numbers.
(a) n = 1, l = 0
(b) n = 3, l = 1
(c) n = 4, l = 2
(d) n = 4, l = 3
Solution:
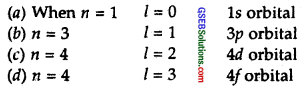
Question 30.
Explain, giving reasons, which of the following sets of quantum numbers are hot possible.
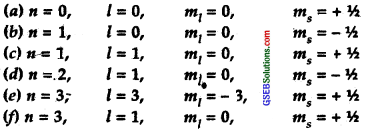
Solution:
(a) Not possible because n cannot be = 0.
(b) When n = l, l = 0, m1 = 0 ms = + \(\frac { 1 }{ 2 }\) is possible
(c) When n = 1, l cannot be = 1, it is not possible.
(d) Possible
(e) When n = 3; Possible values of l can be 0,1,2, therefore l ≠ 3. It is not possible.
(f) n = 3, l = 1, m1 = 0, ms = + \(\frac { 1 }{ 2 }\) is possible
Question 31.
How many electrons in an atom may have the following quantum numbers?
- n = 4 ms = – \(\frac { 1 }{ 2 }\)
- n = 3 l = 0
Solution:
- n = 4; Total electrons possible are 2n2 = 32
- When n = 3, l = 0; Only 2 electrons are possible in 3s.
Question 32.
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de-Broglie wavelength associated with the electron revolving around the orbit.
Solution:
According to the de-Broglie equation
λ = \(\frac { h }{ mv }\)
de-Broglie pointed out such closed orbits can exist only when the circumference of the orbit equals an integral multiple of the wavelength electron.

substituting (i) from de-Borglie equation = 2πr = n\(\frac { h }{ mv }\)
or mvr = n\(\frac { h }{ 2π }\)
i.e., angular momentum is quantized for closed orbits. There is a stationary wave system for the de-Broglie waves for an electron in that orbit and the orbit must contain a whole number of electron waves. Fig. above clearly indicates 3 waves in the third orbit, 6 waves in the sixth orbits, and so on.
Question 33.
What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n =2 of He+ spectrum?
Solution:

which can be so for n1 = 1 and n2 = 2.
This means that n1 = 1 and n2 = 2.
Therefore, the transition is from n = 2 in the case of hydrogen spectrum to n = 1.
Question 34.
Calculate the energy required for the process
He+ (g) → He2+ (g) + e–
The ionization energy for the H atom in the ground state is 2.10 × 10-18 J atom-1.
Solution:
En = \(\frac{2 \pi^{2} m Z^{2} e^{4}}{n^{2} h^{2}}\) for hydrogen like particles
I.E. = Ex – E1 = O – \(\left[\frac{2 \pi^{2} m Z^{2} e^{4}}{h^{2}}\right]\)
= \(\frac{2 \pi^{2} m Z^{2} e^{4}}{h^{2}}\)
For H1Z = 1; I.E. = \(\frac{2 \pi^{2} m Z^{2} e^{4}}{h^{2}}\)
= 2.18 × 10-18J atom-1
For He+, Z = 2 I.E. = 2.18 × 10-18 × 22 J atom-1 = 8.72 × 10-18 J
∴ Energy required for the process He+ (g) → He2+ (g) + e– = 8.72 × 10-18 J
![]()
Question 35.
If the diameter of a carbon atom is 0.15 nm, calculate the number of carbon atoms that can be placed side by side in a straight line across the length of the scale of length 20 cm long.
Solution:
Diameter of a carbon atom = 0.15 nm = 0.15 × 10-9 m
Length of the straight line = 20 cm = 20 × 10-2 m
∴ No. of atoms of carbon which can be placed on 20.0 cm length
= \(\frac{20 \times 10^{-2}}{0.15 \times 10^{-9}}\) = 1.33 × 109
Question 36.
2 × 108 atoms of carbon are arranged side by side. Calculate the radius of the carbon atom if the length of this arrangement is 2.4 cm.
Solution:
No. of atoms of C = 2 × 108
Length of this arrangement = 2.4 cm = 2.4 × 10-2m
∴ Diameter of one carbon atom = \(\frac{2.4 \times 10^{-2}}{2 \times 10^{8}}\) m = 1.2 × 10-10m
∴ Radius of C atom = \(\frac{1.2 \times 10^{-10}}{2}\)
= 0.6 × 10-10m = 0.06 nm
Question 37.
The diameter of the zinc atom is 2.6 Å. Calculate
- the radius of the zinc atom in pm and
- the number of atoms present in a length of 1.6 cm if the zinc atoms are arranged side by side lengthwise.
Solution:
- Diameter of zinc atom = 2.6 Å = 2.6 × 102 pm
radius = \(\frac{2.6 \times 10^{2}}{2}\) = 1.3 × 102 pm = 130 pm - No. of atoms of zinc on 1.6 cm length
\(\frac{1.6 \times 10^{-2}}{2.6 \times 10^{-10}}\) = 0.615 × 108 = 6.15 × 107
Question 38.
A certain particle carries 2.5 × 10-16 C of static electric charge. Calculate the number of electrons present in it.
Solution:
Static electric charge carried by particle = 2.5 × 10-16 C
The charge carried by a single electron = 1.602 × 10-19 C
∴ No. of electrons in the given particle
= \(\frac{2.5 \times 10^{-16}}{1.602 \times 10^{-19}}\) = 1.5605 × 103
Question 39.
In Milikan’s experiment, the static electric charge on the oil drops has been obtained by shining X-rays. If the static electric charge on the oil drop is – 1.282 × 10-18 C, calculate the number of electrons present. it.
Solution:
The static electric charge on oil drop = – 1.282 × 10-18 C
Charge on one electron = – 1.602 × 10-19 C
∴ No. of electrons present in oil drop
= \(\frac{-1.282 \times 10^{-18}}{-1.602 \times 10^{-19}}=8\)
![]()
Question 40.
In Rutherford’s experiment, generally, the thin foil of heavy atoms, like gold, platinum, etc. have been used to be bombarded by the a-particles. If the thin foil of light atoms like aluminum etc. is used, what difference would be observed from the above results?
Solution:
More number of a-particles will pass as the nucleus of the lighter atoms like aluminum is small, a smaller number of a-particles will be deflected as the number of positive charges is less than on the lighter nuclei.
Question 41.
Symbols \(\begin{array}{l}79 \\35\end{array} \mathrm{Br}\)and \({ }^{79} \mathrm{Br}\) can be written, whereas symbols \(\frac{79}{35} \mathrm{Br}\) and \({ }_{35} \mathrm{Br}\) are not acceptable. Answer briefly.
Solution:
For a given element the number of protons is the same for its isotopes whereas the mass number can be different for the given atomic number.
Question 42.
An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
Solution:
Mass no. of the element = 81
Let the no. of protons in it = x
∴ no. of neutrons in it = x + \(\frac { 31.7 }{ 100 }\) x
But Mass number is the sum of protons and neutrons
∴ x + x + \(\frac { 31.7 }{ 100 }\) x = 81
x\(\left(2+\frac{31.7}{100}\right)\) = 81
231.x = 8100 or x = 35
no. of protons = 35 and no. of neutrons = 81 – 35 = 46
∴ The symbol of the element is \(\begin{array}{l}81 \\35 \mathrm{Br}\end{array}\)
Question 43.
An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons, find the symbol of the ion.
Solution:
The mass number of the ion = 37
i.e. no. of protons + no. of neutrons = 37
This ion carries one unit of negative charge.
Let the no. of protons in it = x; no. of electrons = x + 1
no. of neutrons = 37 – x
According to the equation

No. of protons = 17
No. of electrons = 17 + 1 = 18
No.of neutrons = 37 – 17 = 20
This ion is \(\frac{37}{17} \mathrm{Cl}^{-1}\) (chloride ion) and its symbol is \(\frac{37}{17} \mathrm{Cl}^{-1}\)
Question 44.
An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.
Solution:
Mass no. of ion = 56 i.e. n + p = 56
Let the no. of protons = x, no. of neutrons = 56 – x
Since it carries 3 units of positive charge
no of electrons = x – 3
∴According to the question
x – 3 + (x – 3) × \(\frac { 30.4 }{ 100}\) = 56 – x
(x – 3) \(\left[1+\frac{30.4}{100}\right]\) = 56 – x
230.4x – 391.2 = 5600 or x = \(\frac{59912}{230.4}\) = 26
∴ At. no = p = 26
Hence the symbol of the ion will be \(26 \mathrm{Fe}^{3+}\)
![]()
Question 45.
Arrange the following types of radiations in increasing order of frequency:
(a) radiation from the microwave oven
(b) amber light from traffic signal
(c) radiation from FM radio
(d) cosmic rays from outer space and
(e) X-rays.
Solution:
The given radiations in increasing order of frequency
FM < microwave < amber colour < X-rays < cosmic rays
Question 46.
Nitrogen laser produces radiation at a wavelength of 337.1 nm. If the number of photons emitted is 5.6 × 1024, calculate the power of this laser.
Solution:
The wavelength of Nitrogen laser radiation = 337.1 nm
No. of photons emitted (n) = 5.6 × 1024
Power of this laser E = nhv = \(\frac { nhc }{ λ }\)
\(\frac{5.6 \times 10^{24} \times 6.625 \times 10^{-34} \times 3.0 \times 10^{8}}{337.1 \times 10^{-9}}\) J
= 3.3 × 106 J
Question 47.
Neon gas is generally used in the signboards. If it emits strongly at 616 nm, Calculate
- the frequency of emission,
- distance traveled by this radiation in 30 s
- the energy of quantum and
- a number of quanta present if it produces 2 J of energy.
Solution:
(1) Frequency (v) of emission can be calculated as : c = v × λ
where, λ = wavelength = 616 nm = 616 × 10-9 m,
c = velocity of light = 3.0 × 108ms-1
![]()
(2) Distance traveled in 30 seconds
Distance gravelled in 1 second = 3.0 × 108 m
Distance travelled in 30 seconds = 30 × 3.0 × 108 m = 9 × 109 m
(3) Energy of the photon (quantum)
E = hv = 6.625 × 10-34 × 4.87 × 1014J
= 32.26 × 10-20 J
(4) Number of quanta = ![]()
\(\frac{2}{32.26 \times 10^{-20}}\) = 6.2 × 1018
Question 48.
In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 × 1010-18 J from the radiations of 600 nm, calculate the number of photons received by the detector.
Solution:
Energy received by photon detector = 3.15 × 1010-18J
Wavelength of radiations = 600 nm = 600 × 109 m
Now E = nhv = \(\frac { nhc }{ λ }\)
∴ no. of photons received (whole no.)
\(\frac { Eλ }{ hc }\) = \(\frac{3.15 \times 10^{-18} \times 600 \times 10^{-9}}{6.6 \times 10^{-34} \times 3 \times 10^{8}}\) = 10
Question 49.
Lifetimes of the molecules in the excited states are often measured by using a pulsed radiation source of duration nearly in the nanosecond range. If the radiation source has a duration of 2 ns and the number of photons emitted during the pulse source is 2.5 × 1015, calculate the energy of the source.
Solution:
Duration of the radiation source = 2 ns
Period = 2 × 10-9 s
Frequency (v) = \(\frac { 1 }{ period }\) = \(\frac{1}{2 \times 10^{-9}}\) = s-1
= 0.5 × 109s1
No. of photons emitted = 2.5 × 1015
∴ Energy of the source = nhv
= 2.5 × 1013 × 6.626 × 10-34 × 0.5 × 109 J
= 8.28 × 10-10 J.
Question 50.
The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each transition and energy difference between two excited states.
Solution:
To find frequency (v1); λ1 = 589 nm = 589 × 10-9 m [Given]
To find frequency (v2); λ2 = 589.6 nm = 589.6 × 10-9 m [Given]

Energy = hv
E1 = hv1 E2 = hv2
∴ △E – E1 – E2 = h(v1 – v2)
= 6.625 × 10-34 × 0.0053 × 1014 = 0.035 × 10-20
= 3.46 × 10-22 J Or 3.5 × 10-22 J
Question 51.
The work function for the cesium atom is 1.9 eV. Calculate
(a) the threshold wavelength and
(b) the threshold frequency of the radiation. If the cesium element is irradiated with a wavelength of 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.
Solution:
W0 = work function for caesium = 1.9 eV= 1.9 × 1.602 × 10-19 J [1 eV= 1.602 × 10-19J]
W0 = hv0, where v0 = threshold frequency
∴ v0 = \(\frac{W_{0}}{h}\) = \(\frac{1.9 \times 1.602 \times 10^{-19}}{6.625 \times 10^{-34}}\) s-1
(b) ∴ threshold frequency = 0.4594 × 1015 s-1 = 4.59 × 1014 s-1
(a) Threshold wavelength λ0 = \(\frac{c}{v_{0}}\) = \(\frac{3 \times 10^{8}}{4.59 \times 10^{14}}\) = 0.6536 × 10-6m = 654 nm
kinetic energy = hv – W0 = \(\frac { hc }{ λ }\) – W0
\(\frac{6.625 \times 10^{-34} \times 3.0 \times 10^{8}}{500 \times 10^{-9}}\) – 3.04 × 10-19
= 3.957 × 10-19 – 3.04 × 10-19 = 0.935 × 10-19 J
K.E = \(\frac { 1 }{ 2 }\) mv2
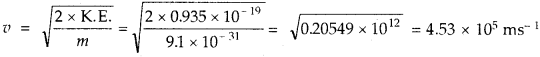
Question 52.
Following results are observed when sodium metal is irradiated with different wavelengths. Calculate
(a) threshold wavelength and,
(b) Planck’s constant.
![]()
Solution:
![]()
mass of electron, m = 9.1 × 10-31 kg
Here λ = 500 × 10-9 m
vmax = 2.55 × 105 ms-1
λ0 = ?
using equation \(\frac{h c}{\lambda_{0}}\) = \(\frac { 1 }{ 2 }\)mv2 max = \(\frac { hc }{ λ }\),We get
Substituting the given results of the three experiments, we get
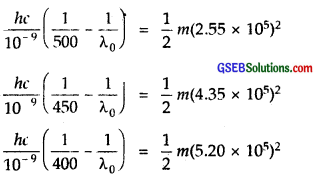
Dividing (ii) by (i)
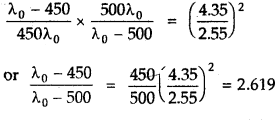
or λ0 = 2.619λ – 1309.5 + 450
or 1.619λ0 = 859.5
or λ0 = 531 nm
Substituting this value of λ0 in (iii)
\(\frac{h \times\left(3 \times 10^{8}\right)}{10^{-9}}\)\(\left(\frac{1}{400}-\frac{1}{531}\right)\) = \(\frac { 1 }{ 2 }\)(9.11 × 10-31) × (5.20 × 105)2
or on sloving h = 6.66 × 10-34 Js
Question 53.
The ejection of the photoelectron from the silver medal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for the silver medal.
Solution:
h = 6.62 × 10-34 Js
V0 = 0.35 volt
e = 1.6 × 10-19C
λ = 256.7 × 10-9m
w = ? (eV)
Using equation eV0 = \(\frac { 1 }{ 2 }\)\(m v_{\max }^{2}\) We get
\(\frac { 1 }{ 2 }\)\(m v_{\max }^{2}\) = 1.6 × 10-19 × 0.35 J = 0.56 × 10-19J
= \(\frac{56 \times 10^{-19}}{1.6 \times 10^{-19}}\) eV = 0.35 eV.
Also according to Einstein’s photo electric equation,
\(\frac { hc }{ λ }\) = w + \(\frac { 1 }{ 2 }\)\(m v_{\max }^{2}\)
or w = \(\frac { hc }{ λ }\) – \(\frac { 1 }{ 2 }\)\(m v_{\max }^{2}\)
= \(\frac{6.62 \times 10^{-34} \times 3 \times 10^{8}}{256.7 \times 10^{-9}}\) – 0.35 eV
= 4.83 eV – 0.35 eV = 4.48 eV
Question 54.
If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5 × 107 ms-1, calculate the energy with which it is bound to the nucleus.
Solution:
λ = 150 pm = 150 × 10-12m
v = velocity = 1.5 × 107 ms-1
∴ Kinetic energy of the ejected electron
= \(\frac { 1 }{ 2 }\)mv2 = \(\frac { 1 }{ 2 }\) × 9.1 ×10-31 × (1.5 × 107)2J
= 0.102 × 10-19J
Energy of the striking photon E
= hv = \(\frac { λc }{ λ }\)
\(\frac{6.625 \times 10^{-34} \times 3.0 \times 10^{8}}{150 \times 10^{-12}}\) J
= 1.325 × 10-15 J
∴ The minimum energy required to eject the electron
E0 = E – K.E. of the ejected electron
= (1.325 × 10-15 – 0.102 × 10-15)J
= 1.223 × 10-15 J = \(\frac{1.223 \times 10^{-15}}{1.602 \times 10^{-19}}\) eV [∵1J = 1.602 × 10-19 eV]
= 7.6 × 103 eV
∴ The energy with which the electron is bound to the nucleus = 7.6 × 103 eV
Question 55.
Emission transitions in the Paschen series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 × 1015 (Hz) [1/32 – 1/n2]
Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
Solution:
According to the question
v = 3.29 × 1015 (Hz) \(\left[\frac{1}{3^{2}}-\frac{1}{n^{2}}\right]\)

∴ The electron jumps from n = 5 to n = 3.
Since this is a transition occurring in the paschal series and paschal series lie in the infra-red portion of light.
∴ The region of the spectrum is in infra-red, which can also be calculated from the wavelength λ.
Question 56.
Calculate the wavelength for the emission transition if it starts from the orbit having a radius of 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Solution:
Radius of nth orbit of H-like particle = \(\frac{0.529 n^{2}}{Z}\) pm
r1 = 1.3225 nm = 52.9 n12,r2 = 211.6 pm = 52.9 n22 as Z = 1
∴ \(\frac { r1 }{ r2 }\) = \(\frac { 1322.5 }{ 211.6 }\) = \(\frac{n_{1}^{2}}{n_{2}^{2}}\)
or \(\frac{n_{1}^{2}}{n_{2}^{2}}\) = 6.25 or \(\frac { n1 }{ n2 }\) = 2.5
∴ If n2 = 2, n1 = 5
since this is the transition from n2 = 5 to n1 = 2, this transition belongs to the Balmer series
\(\bar{v}\) = 1.097 × 107\(\left(\frac{1^{\prime}}{2^{2}}-\frac{1}{5^{2}}\right)\) m-1
= 1.097 × \(\frac { 21 }{ 100 }\) × 107m-1
or λ = \(\frac { 1 }{ \bar{v} }\) = \(\frac{100}{1.097 \times 21 \times 10^{7}}\) m
= 434 × 10-9m = 434 nm
∴ It lies in the visible region.
![]()
Question 57.
The dual behavior of matter proposed by de Broglie led to the discovery of an electron microscope often used for the highly magnified images of biological molecules and another type of material. If the velocity of the electron in the microscope is 1.6 × 106 ms-1 calculate de Broglie wavelength associated with this electron.
Solution:
de-Broglie wavelength is λ
λ = \(\frac{h}{m \times v}\)
where h = planck’s constant, m = mass of electron,
v = velocity of electron
λ = \(\frac{6.625 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.6 \times 10^{6}}\) = 0.455 × 10-9m = 4.55 pm
Question 58.
Similar to electron diffraction, a neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
Solution:
λ = 800 pm = 800 × 10-12 m
Mass of the neutron = 1.675 × 10-27 kg
λ = \(\frac { h }{ mv }\) or v = \(\frac { h }{ mλ }\)
v = \(\frac{6.626 \times 10^{-34}}{1.675 \times 10^{-27} \times 800 \times 10^{-12}}\) = 4.94 × 104 ms-1
Question 59.
If the velocity of the electron in Bohr’s first orbit is 2.19 × 106 ms-1 calculate the de Broglie wavelength associated with it.
Solution:
Velocity of electron in Bohr’s first orbit v = 2.19 × 10106 ms-1
h = 6.625 × 10-34 Js
mass of electron = m = 9.1 × 10-31 kg
∴ de Broglie wavelength (λ) = \(\frac{h}{m \times v}\)
= \(\frac{6.625 \times 10^{-34}}{9.1 \times 10^{-31} \times 2.19 \times 10^{6}}\)m
= 0.332 × 10-9 m
= 0.332 × 10-9
= 332 × 10-12m = 332 pm
Question 60.
The velocity associated with a proton moving in a potential difference of 1000 V is 4.37 × 105 ms-1If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
Solution:
Velocity of the hockey ball (v) = 4.37 × 105 ms-1
Mass of the ball = 0.1 kg
∴ λ (wavelength) = \(\frac { h }{ m × v }\)
= \(\frac{6.625 \times 10^{-34}}{0.1 \times 4.37 \times 10^{5}}\) m = 1.51 × 10-38m
Question 61.
If the position of the electron is measured within an accuracy of ± 0.002 nm; calculate the uncertainty in the momentum of the electron. Suppose the momentum of the electron is h/4πm × 0.05 nm, is there any problem in defining this value.
Solution:
△x × △p = \(\frac { h}{ 4π }\)
0.002 × 10-9 × △p = \(\frac{6.625 \times 10^{-34} \times 7}{4 \times 22}\)
△p = \(\frac{6.625 \times 10^{-34} \times 7}{4 \times 22 \times 0.002 \times 10^{-9}}\)
= 2.63 × 10-23 kg ms-1
Actual momentum = \(\frac{h}{4 \pi \times 0.05}\) nm = \(\frac{6.625 \times 10^{-34}}{4 \times 3.14 \times 5 \times 10^{-11}}\)
= 1.055 × 10-24 kg ms-1
This value cannot be defined as the actual magnitude of the momentum smaller than the uncertainty.
Question 62.
The quantum numbers of six electrons are given below. Arrange them in order of increasing energies. If any of these combination(s) has/have the same energy lists :
1. n = 4, l = 2, m1 = -2, ms = – 1/2
2. n = 3, l = 2, m1 = 1, ms = + 1/2
3. n = 4, l = 1, m1 = 0, ms = + 1/2
4. n = 3, l = 2, m1 = -2, ms = – 1/2
5. n = 3, l = 1, m1 = -1, ms = + 1/2
6. n = 4, l = 1, m1 = 0, ms = + 1/2
Solution:
5 < 2 = 4 < 6 = 3 < 1
![]()
Question 63.
The bromine atom possesses 35 electrons. It contains 6 electrons in 2p orbital, 6 electrons in 3p orbital and 5 electron in 4p orbital. Which of these electron experiences the lowest effective nuclear charge?
Solution:
As we go away from the nucleus, effective nuclear pull goes on decreasing. Hence electrons present in 4p orbital experience the lowest effective nuclear charge.
Question 64.
Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?
- 2s and 3s
- 4d and 4f
- 3d and 3p
Solution:
- 2s, as it is nearer the nucleus
- Ad
- 3p
Question 65.
The unpaired electrons in Al and Si are present in the 3p orbital. Which electrons will experience a more effective nuclear charge from the nucleus?
Solution:
The unpaired electrons present in Aluminium and Silicon are in 3p1 and 3p2 orbitals. Due to more nuclear charge in the case of Si [14p] than in Al [13p], electrons in Si will experience more nuclear charge than Al.
Question 66.
Indicate the number of unpaired electrons in :
- P
- Si
- Cr
- Fe and
- Kr
Solution:
- P has 3 unpaired electrons [P = [Ne]3s23p3]
- Si has 2 unpaired electrons [Si = [Ne] 3s23p2]
- Cr = 24 = [Ar] 3d5s1 has 6 unpaired electrons.
- Fe = 26 = [Ar] 3d64s2 has 4 unpaired electrons.
- Kr = 36 = [Ar] 3d104s24p6 has no unpaired electrons.
Question 67.
(a) How many sub-shells are associated with n = 4?
(b) How many electrons will be present in the sub-shells having an ms value of – 1/2 for n = 4?
Solution:
When n = 4
l = 0, 1, 2, 3

(b) No. of electrons present in the subshells having ms value of – \(\frac { 1 }{ 2 }\) for n = 4 are 16.