Gujarat Board GSEB Textbook Solutions Class 11 Physics Chapter 13 Kinetic Theory Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Physics Chapter 13 Kinetic Theory
GSEB Class 11 Physics Kinetic Theory Text Book Questions and Answers
Question 1.
Estimate the fraction of molecular volume to the actual volume occupies by oxygen gas at STP. Take the radius of an oxygen molecule to be roughly 3Å?
Answer:
A gram, mole of oxygen gas occupies a volume at S.T.P.,
V = 22400 × 10-6m3 (∵ 1 ml = 1 cm3)
r = Radius of an oxygen molecule = 3Å = 3 × 10-10 m
Molecular volume of one mole of oxygen, V’
= Volume of one molecule of O2 × Avogadro’s number (N)
= \(\frac{4}{3}\)πr3 × N
or V’ = \(\frac{4}{3}\)π × (3 × 10-10)3 × 6.023 × 1023
∴ Fraction of molecular volume of the actual volume occupied by oxygen = Ratio of two volumes
= \(\frac{V}{V’}\)

= 4 × 10-4
![]()
Question 2.
Molar volume is the volume occupied by 1 mole of any (ideal) gas at standard temperature and pressure (STP : 1 atmospheric pressure, 0°C). Show that it is 22.4 litres.
Answer:
Here, at STP conditions
P = 1 atm = 7.6 m of Hg column
= 0.76 × 13.6 × 103 × 9.8
= 1.013 × 105 Nm-2
T = 0°C = 273 K
R = 8.31 J mol-1 K-1
n = 1 mole, To prove V = 22.4 litre
∴ Using the gas equation,
PV = nRT, we get
V = \(\frac{nRT}{P}\) = \(\frac{1 \times 8.31 \times 273}{1.013 \times 10^{5}}\)
= 22.4 × 10-3m3 = 22.4 litre.
Hence proved.
![]()
Question 3.
Figure below shows plot of PV/T versus P for 1.00 × 10-3 kg of oxygen gas at two different temperatures?

(a) What does the dotted plot signify?
(b) Which is true T1 > T2 or T1 > T2?
(c) What is the value of PV/T where the curves meet on the Y-axis?
(d) If we obtained similar plots for 1.00 × 10-3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the Y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low pressure – high temperature region of the plot)? Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mol-1 K-1).
(a) The dotted plot corresponds to ‘ideal’ gas behaviour as it is parallel to P-axis and it tells that value of PV/T remains same (= nR) even when P is changed.
(b) The upper position of PV/T shows that its value is lesser for T1, thus T1 > T2. This is because the curve at T1 is more close to dotted plot than the curve at T2. Since the behaviour of a real gas approaches the perfect gas behaviour, as the temperature is increased.
(c) Where the curve meets PV/T axis, the ideal gas curve also meets the same as PV = nRT applicable at this point i.e. if the amount of gas under consideration is 1 mole, then the value of PV/T will be R(= 8.31 J mol-1k-1).
∴ The value of \(\frac{PV}{T}\) = nR
To find n:
We know that 3.2 × 10-3 kg of O2 = 1 mole
∴ 1.00 × 10-3 kg of O2 = \(\frac{1}{32 \times 10^{-3}}\) × 1 × 103
i.e. n = \(\frac{1}{32}\)
R = 8.32 JK-1 mol-1
∴ \(\frac{PV}{T}\) = \(\frac{1}{32}\) × 8.31 = 0.26 JK-1.
(d) No, the same value of PV/T will not be obtained for H2 as its value depends on mass and mass of H2 is lesser than O2.
Let m kg be the required mass of hydrogen which yields the same value of PV/T.
∴ n = \(\frac{\mathrm{m}}{2.02 \times 10^{3}}\) ………………. (i)
for \(\frac{PV}{T}\) = nR = 2.26 JK-1, n is given by
n = \(\frac{0.26}{R}\) = \(\frac{0.26 \mathrm{JK}^{1}}{8.31 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}}\)
= 0.0313 mol ……………………. (ii)
∴ From (i) and (ii), we get
m = 2.02 × 10-3 n
= 2.02 × 10-3 × 0.313
= 0.0632 × 10-3 kg
= 6.32 × 10-5 kg.
![]()
Question 4.
An oxygen cylinder of volume 30 litres has anlnitial gauge pressure of 15 atm and a temperature of 27°C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17°C. Estimate the mass of oxygen taken out of the cylinder. (R = 8.31 JK-1 mol-1, molecular mass of O2 = 32 u.)
Answer:
Here, initially in the oxygen cylinder,
V1 = 30 litres
= 30 × 10-3 m3
P1 = 15 atm = 15 × 1.013 × 105 Pa
T1 = 27+ 273
= 300 K
R = 8.31 JK-1 mol-1
If n1 be the moles of oxygen gas contained in the cylinder, then using the gas equation PV = nRT, we get
n = \(\frac{P_{1} V_{1}}{R T_{1}}\) = \(\frac{15 \times 1.013 \times 10^{5}}{8.31 \times 300}\)
= 18.253
For oxygen, molecular weight,
M = 32 g = 32 × 10-3 kg
= 584.1 × 10-3 kg
Finally in the oxygen cylinder let n, moles of oxygen be left
Here, V2 = 30 × 10-3 m3
P2 = 11 atm= 11 × 1.013 × 105 Pa
T2 = 17+ 273
= 290 K
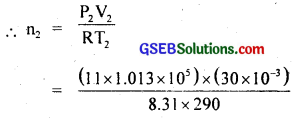
= 13. 847
∴ Final mass of oxygen gas in the cylinder,
m2 = 13.847 × 32 × 103
= 453.1 × 10-3 kg
∴ Mass of oxygen taken out of the cylinder
= m1 – m2
= (584.1 – 453.1) × 10-3 kg
= 141 × 103 kg
= 0.141 kg.
Question 5.
An air bubble of volume 1.0 cm3 rises from the bottom of a lake 40 m deep at a temperature of 12°C. To what volume does it grow when it reaches the surface, which is at a temperature 35°C?
Answer:
When the air bubbles is at a depth of 40 m,
then V1 = 1.0 cm3
= 1.0 × 106 m3
T1 = 12°C = 12 + 273 = 285 K
P1 = 1 atm + 40 m depth of water
= 1 atm + h1ρg
= 1.013 × 105 + 40 × 103 × 9.8
= 493000 Pa = 4.93 × 105 Pa.
When the air bubble reaches at the surface of lake, then
V2 = ?
T2 = 35°C
= 35 + 273
= 308 K
P2 = 1 atm
= 1.013 × 105 Pa

= 5. 275 × 10-6m3
= 5.3 × 106m3.
![]()
Question 6.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27°C and 1 atm pressure.
Answer:
Here, V = 25.0 m3
T = 27°C = 27 + 273
= 300 K
k = 1.38 × 1023 JK-1
P = 1 atm
= 1.013 × 105 Pa
Now the gas equation, PV = nRT may be written as
P = \(\frac{nRT}{V}\)
= \(\frac{n}{V}\)(Nk)T (∵ \(\frac{R}{N}\) = k)
= (nV) \(\frac{kT}{V}\) = N \(\frac{kT}{V}\)
Where N’ = nN = total number of air molecules in the given gas
∴ N’ = \(\frac{PV}{kT}\) = \(\frac{\left(1.013 \times 10^{5}\right) \times 25}{1.38 \times 10^{-23} \times 300}\)
= 6.10 × 1026.
Question 7.
Estimate the average thermal energy of helium atom of
- room temperature (27°C),
- the temperature on the surface of the Sun (6000 K),
- the temperature of 10 million kelvin (the typical core temperature in the case of a star).
Answer:
According to kinetic theory of gases, the average kinetic energy of the gas at a temperature T (i.e. average thermal energy) is given by
E = \(\frac{3}{2}\) kT
Here k = 1.38 × 1023 JK-1.
Now
1. At T = 27°C = 273 + 27 = 300 K
E = \(\frac{3}{2}\) × 1.38 × 10-23 × 300
= 621 × 1023 J
= 6.21 × 1023 J.
2. Here, T = 6000 K
∴ E = \(\frac{3}{2}\) × 1.38 × 10-23 × 6000
= 1.24 × 1019 J
3. Here T = 10 × 106 K = 107 K
∴ E = \(\frac{3}{2}\) × 1.38 × 10-23 × 107
= 2.07 × 1016J = 2.1 × 10-16 J.
![]()
Question 8.
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monoatomic gas) the secqnd contains chlorine (diatomic) and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is vrms the largest?
Answer:
Yes. According to Avogadro’s hypothesis, the condition of temperature and pressure remain same, the equal volumes of all gases have equal number of molecules. So the number of molecules in the three vessels containing different gases must be same i.e. the three vessels contain equal no. of respective molecules.
No. r.m.s. speed of molecules is not same in three cases as explained below:
We know that the rms velocity of a gas is given by:
Vr.m.s = \(\sqrt{\frac{3 R T}{M}}\) or Vr.m.s ∝ \(\frac{1}{\sqrt{\mathrm{M}}}\) where M = Molecular mass and is different gases, therefore Vr.m.s of three gases will be different.
As Vr.m.s is inversely proportional to mass of molecules of the gas and since neon is the lightest of the three gases, therefore Vr.m.s for neon gas is largest.
Question 9.
At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at – 20°C? (Atomic mass of Ar = 39.9 u of He = 4.0 u).
Answer:
Let C1 and C2 be the r.m.s. speed of argon and helium gas atoms at temperature T1 and T2 respectively.
Here, M1 = 39.9 × 103 kg
M2 = 4.0 × 10-3 kg
T1 = ?
T2 = – 20 + 273
= 253 K
Now we know that r.m.s. speed is given by

or T = 2523.7 K = 2524 K
= 2.524 × 103 K.
![]()
Question 10.
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nigrogen at 2.0 atm and temperature 17°C. Take the radius of a nitrogen molecule to be roughtly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (molecular mass of N2 = 28.0 u).
Answer:
According to Maxwell’s correction, the mean free path (λ) of a gas molecule is given by
λ = \(\frac{1}{\sqrt{2} \pi \mathrm{nd}^{2}}\)
where d = diameter of a molecule
and n = \(\frac{N}{V}\) = image 6
At 2 atm pressure, the volume of the gas of mass M is given by
V = \(\frac{RT}{P}\)
T = 273 + 17° = 290 K
∴ n = \(\frac{N}{V}\) = \(\frac{N.P}{RT}\)
Now N = 6.023 × 1023 mol-1
P = 2 atm = 2 × 1.013 × 105 Nm-2
R = 8.3 JK-1 mol-1

The r.m.s. velocity is given by
C = \(\sqrt{\frac{3 R T}{M}}\)
Putting R = 8.31 J mol-1 k-1
T = 290 K
M = 28 × 10-3 kg
we get, C = \(\sqrt{\frac{3 \times 8.31 \times 290}{28 \times 10^{-3}}}\) = 5.08 × 102 ms-1
= 5.10 × 102 ms-1
∴ Collision frequency (v) is given by
v = \(\frac{C}{λ}\) = \(\frac{5.1 \times 10^{2}}{1.0 \times 10^{-7}}\) = 5.1 × 109s-1
Ler τ be the time between two successive collisions
∴ τ = \(\frac{λ}{C}\) = \(\frac{1.0 \times 10^{-7} \mathrm{~m}}{5.1 \times 10^{2} \mathrm{~ms}^{-1}}\)
= 2.0 × 10-10s ……………………….. (i)
Also let t = time taken for the collision,
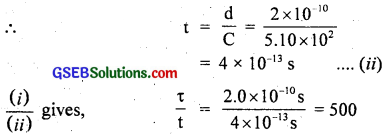
or τ = 500 t i.e. the time taken between successive collisions is 500 times the time taken for a collision to take place i.e. the two molecules are in contact. This shows that the molecule in a gas moves nearly free for most of the time.