Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.2
In questions 1 to 7, find the equations of the line, which satisfy the given conditions:
1. Write the equations for x and y-axis.
2. passing through (- 4, 3) with slope \(\frac{1}{2}\).
3. Passing through (0, 0) with slope m.
4. Passing through (2, 2\(\sqrt{3}\)) and inclined with the x-axis at an angle of 75°.
5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope – 2.
6. Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
7. Passing through the points (- 1, 1) and (2, – 4).
Solutions to questions 1 to 7:
1. Equation of the x-axis is y = 0.
Equation of the y-axis is x = 0.
![]()
2. Equation of a line passing through (x1, y1) with slope m is (y – y1) = m(x – x1).
Here, x1 = – 4, y1 = 3, m = \(\frac{1}{2}\).
∴ Equation of the required line is
(y – 3) = \(\frac{1}{2}\) (x + 4)
or 2y – 6 = x + 4 or x – 2y + 10 = 0
3. x1 = 0, y1 = 0, Slope = m.
Equation of the required line is
(y – 0) = m(x – 0)
or y = mx.
![]()
4. Here, x1 = 2, y1 = 2\(\sqrt{3}\)
m = tan 75° = tan (45° + 30°)
= \(\frac{tan 45° + tan 30°}{1 – tan 45° tan 30°}\) [∵ tan(A + B) = \(\frac{tan A + tan B}{1 – tan A tan B}\)

Equation of the required line is
y – 2\(\sqrt{3}\) = \(\frac{\sqrt{3}+1}{\sqrt{3}-1}\) (x – 2).
(\(\sqrt{3}\) – 1)y – 2\(\sqrt{3}\)(\(\sqrt{3}\) – 1) = (\(\sqrt{3}\) + 1)x – 2(\(\sqrt{3}\) + 1)
or (\(\sqrt{3}\) – 1)y – 6 + 2\(\sqrt{3}\) = (\(\sqrt{3}\) + 1)x – 2\(\sqrt{3}\) – 2.
or (\(\sqrt{3}\) + 1)x – (\(\sqrt{3}\) – 1)y = – 6 + 2\(\sqrt{3}\) + 2\(\sqrt{3}\) + 2.
= 4\(\sqrt{3}\) – 4 = 4(\(\sqrt{3}\) – 1).
∴ Then, equation of required line is
(\(\sqrt{3}\) + 1)x – (\(\sqrt{3}\) – 1)y = 4(\(\sqrt{3}\) – 1).
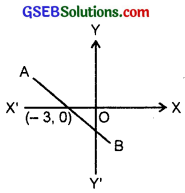
5. The line AB meets x-axis at (- 3, 0) and slope of the line = – 2.
∴ Equation of the line is y – 0 = – 2(x + 3)
or 2x + y + 6 = 0.
![]()
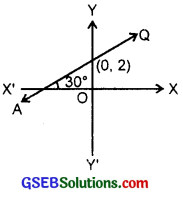
6. The line PQ intersects y-axis at (0, 2).
Slope of PQ = tan 30° = \(\frac{1}{\sqrt{3}}\)
Equation of PQ is
y – 2 = \(\frac{1}{\sqrt{3}}\)(x – 0).
or \(\sqrt{3y}\) – 2\(\sqrt{3}\) = x
or x – \(\sqrt{3}\)y + 2\(\sqrt{3}\) = 0.
7. The line passes through the points A(- 1, 1) and B(2, – 4). Equation of the line passing through (x1, y1) and (x2, y2) is
y – y1 = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)(x – x1)
Here, x1 = – 1, y1 = 1, x2 = 2, y2 = – 4.
∴ Equation of AB is
y – 1 = \(\frac{-4-1}{2+1}\)(x + 1) = \(\frac{-5}{3}\)(x + 1).
or 3(y – 1) = – 5(x + 1).
or 3y – 3 = – 5x – 5.
or 5x + 3y – 3 + 5 = 0
or 5x + 3y + 2 = 0.
![]()
Question 8.
Find the equation of a line whose perpendicular distance from the origin is 5 units and the angle made by the perpendicular with positive x-axis is 30°.
Solution:
If a line is at a distance p from the origin and perpendicular makes an angle to with positive direction of x-axis, its equation is
xcos ω + ysin ω – p.
Here, p = 5, ω = 30°.
∴ Equation of the required line is
x cos 30° + y sin 30° = 5.
or \(\frac{\sqrt{3}}{2}\)x + \(\frac{1}{2}\)y = 5
or \(\sqrt{3x}\) + y = 10.
Question 9.
The vertices of a triangle PQR are P(2, 1), Q(- 2, 3) and R(4, 5). Find the equation of the median through the vertex R.
Solution:
The vertices P and Q are (2,1) and (- 2, 3).
The middle point of PQ is S (\(\frac{2-2}{0}\), \(\frac{1+3}{2}\)) or S(0, 2).
∴ Equation of the median RS, where R is (4, 5) and S is the point (0, 2) is
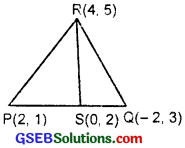
y – 5 = \(\frac{2-5}{0-4}\)(x – 4).
[Apply formula y – y1 = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)(x – x1)
or y – 5 = \(\frac{-3}{-4}\)(x – 4).
or 4(y – 5) = 3(x – 4) or 4y – 20 = 3x – 12.
i.e; 3x – 4y = – 20 + 12 – 8
∴ Equation of median RS is 3x – 4y + 8 = 0.
![]()
Question 10.
Find the equation of the line passing through the point (- 3, 5) and perpendicular to the line through the points (2, 5) and (- 3, 6).
Solution:
Slope of the line joining A(2, 5) and B(- 3, 6) = \(\frac{6-5}{-3-2}\) = \(\frac{1}{-5}\).
∴ m = slope of any line ⊥ to AB = 5 [m1 = \(\frac{-1}{m_{2}}\).
The equation of the line passing through (- 3, 5) and perpendicular to AB is
y – 5 = 5(x + 3)
⇒ 5x – y + 20 = 0.
Question 11.
A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1 : n. Find the equation of the line.
Solution:
Slope of the line joining the points A(1, 0) and B(2, 3)
= \(\frac{3-0}{2-1}\) = \(\frac{3}{1}\) = 3.
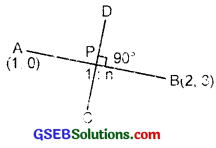
∴ Slope of the CD perpendicular to AB = – \(\frac{1}{3}\) [The lines are ⊥, so m1m2 = – 1]
The point P divides AB in the ratio 1 : n.
∴ Coordinates of P are
(\(\frac{1×2+1×n}{1+n}\), \(\frac{1×3+0×n}{1+n}\)) or (\(\frac{n+2}{n+1}\), \(\frac{3}{n+1}\)).
∴ Equation of the line CD which is ⊥ to AB and passes through P is
y – \(\frac{3}{n+1}\) = – \(\frac{1}{3}\)(x – \(\frac{n+2}{n+1}\))
[Using the formula y – y1 = m(x – x1)]
or 3(n + 1)y – 9 = – (n + 1) (x – \(\frac{n+2}{n+1}\))
= – (n + 1)x + (n + 2)
or (n + 1)x + 3(n + 1)y = n + 2 + 9
or (n + 1)x + 3(n + 1)y = r + 11.
![]()
Question 12.
Find the equation of a line that cuts off equal intercepts on the co-ordinate axes and passes through (2, 3).
Solution:
The line making equal intercepts has the slope either 1 or – 1.
∴ tan 45° – 1
or tan 135° = – 1.
Now(i) slope = 1, P(2, 3)
∴ Equatirn of the line PR of slope 1 and passing through P(2, 3) is
y – 3 – 1(x – 2)
[Using the formula y – y1 = m(x – x1)]
or x – y + 1 = 0.
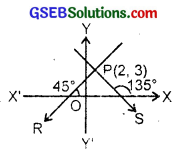
(ii) When the slope = – 1.
Equation of the lire with slope – 1 and passing through P(2, 3) is
y – 3 = – 1 × (x – 2).
or x + y – 3 – 2 = 0,
or x + y – 5 = 0.
![]()
Question 13.
Find the equations of the lines passing through the point (2, 2), such that the sum of their intercepts on the axes is 9.
Solution:
Let the intercepts along x-axis and y-axis be a and b.
∴ a + b = 9.
or b = 9 – a …………….. (1)
∴ Equation of the line in intercepts form is
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1 ………………….. (2)
⇒ \(\frac{x}{a}\) + \(\frac{y}{9-a}\) = 1 [Using (1)]
Since point A(2, 2) lies on it, therefore
\(\frac{2}{a}\) + \(\frac{2}{9-a}\) = 1.
⇒ \(\frac{2(9-a)+2a}{a(9-a)}\) = 1.
⇒ 18 – 2a + 2a = a(9 – a)
⇒ 18 = 9a – a2
⇒ a2 – 9a + 18 = 0 ⇒ (a – 3)(a – 6) = 0.

Hence, the required equations of straight lines are 2x + y = 6 and x + 2y = 6.
![]()
Question 14.
Find the equation of the line through the point (0, 2) making an angle \(\frac{2π}{3}\) with the positive x-axis. Also, find the equation of the line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
Solution:
Slope of the line = tan \(\frac{2π}{3}\)
= tan (π – \(\frac{π}{3}\))
= – \(\frac{π}{3}\) = – \(\sqrt{3}\).
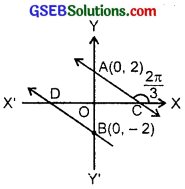
Equation of the line AC passing through (0, 2) and having the slope – \(\sqrt{3}\) is
y – 2 = – \(\sqrt{3}\) (x – 0).
[Using the formula y – y1 = m(x – x1)]
⇒ \(\sqrt{3}\)x + y – 2 = 8.
Another line BD is parallel to AC.
∴ Slope of BD = Slope of AC = – \(\sqrt{3}\).
BD is passing through the point B(0, – 2).
∴ Equation of BD is
y + 2 = – \(\sqrt{3}\)(x – 0).
or \(\sqrt{3x}\) + y + 2 = 0.
Thus, equations of AC and BD are
\(\sqrt{3x}\) + y – 2 = 0 and \(\sqrt{3x}\) + y + 2 = 0.
![]()
Question 15.
The perpendicular from the origin to a line meets at the point (- 2, 9). Find the equation of the line.
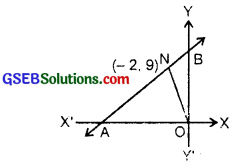
Solution:
Let ON be the perpendicular to AB.
The point N is (- 2, 9).
∴ Slope of ON = \(\frac{9-0}{-2-0}\) = \(\frac{- 9}{2}\) [Slope = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)]
Slope of AB which is ⊥ ON = \(\frac{2}{9}\) [∵ Lines are ⊥ if m1m2 = – 1]
Now AB passes through (- 2, 9) and has the slope \(\frac{2}{9}\)
∴ Equation of AB is y – 9 = \(\frac{2}{9}\)(x + 2) [y – y1 = m(x – x1)]
or 9y – 81 = 2x + 4
or 2x – 9y + 85 = 0.
Question 16.
The length L (in centimetres) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942, when C = 20 and L = 125.134, when C = 110, express L in terms of C.
Solution:
L is a linear function of C.
∴ L = a + bC.
For L = 124.942, C = 20.
∴ 124.942 = a + 20b …………….. (1)
For L = 125.134, C = 110.
∴ 125.134 = a + 110b …………….. (2)
Subtracting (1) from (2), we get
0.192 = 90b.
∴ b = \(\frac{0.192}{90}\) = 0.00213.
From (1), 124.942 = a + 20 × 0.00213
= a + 0.0426.
∴ a = 124.942 – 0.0426
= 124.8994.
Now, L in terms of C is
L = a + bC
⇒ L = 124.8994 + 0.00213C
![]()
Question 17.
The owner of a milk store finds that he can sell 980 litres of milk each week at ₹ 14/litre and 1220 litres of milk each week at ₹ 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at ₹ 17/litre.
Solution:
Let y litres milk is sold at ₹ x/litre.
x and y have linear relationship, i.e.,
y = a + bx, i.e., it is a straight line.
Now, y1 = 980 litres, x1 = ₹ 14/litre.
y2 = 1220 litres, x2 = ₹ 16/litre.
Slope of the line = \(\frac{1220 – 980}{16 – 14}\) = \(\frac{240}{2}\) = 120.
∴ Equation of the line is
y – 980 = 120(x – 14).
When x = 17, y = 980 + 120(17 – 14)
= 980 + 120 × 3
= 980 + 360 = 1340.
Hence, 1340 litres milk may be sold at ₹ 17/litre.
![]()
Question 18.
P(a, b) is the mid-point of a line segment between axes. Show that the equation of the corresponding line is \(\frac{x}{a}\) + \(\frac{x}{b}\) = 2.
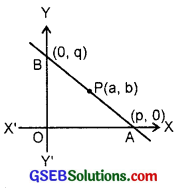
Solution:
Let the line AB makes intercepts p and q on the axes.
∴ A is (p, 0) and B is (0, q).
Now, P(a, b) is the mid-point of AB.
∴ \(\frac{p+0}{2}\) = a, \(\frac{0+q}{2}\) = b.
∴ p = 2a, q = 2b.
Intercepts form of the line AB
\(\frac{x}{p}\) + \(\frac{x}{q}\) = 1.
or \(\frac{x}{2a}\) + \(\frac{y}{2b}\) = 1 or \(\frac{x}{a}\) + \(\frac{y}{b}\) = 2.
Question 19.
Point (h, k) divides a line segment between the axes in the ratio 1 : 2. Find equation of the corresponding line.
Solution:
Let the line AB makes intercepts a and b on the axes. The point R(h, k) divides line segment AB in the ratio 1 : 2.
So, h = \(\frac{1×0+2×a}{1+2}\)
= \(\frac{2a}{3}\)
∴ a = \(\frac{3}{2}\)h
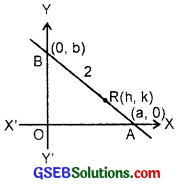
and k = \(\frac{1×b+2×0}{1+2}\) = \(\frac{b}{3}\).
∴ b = 3k.
Intercepts form of the line AB is
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1.
or \(\frac{x}{3/2h}\) + \(\frac{y}{3k}\) = 1 or \(\frac{2x}{3h}\) + \(\frac{y}{3k}\) = 1.
or 2kx + hy = 3kh.
![]()
Question 20.
By using the concept of equation of a line, prove that the three points (3, 0), (- 2, – 2) and (8, 2) are collinear.
Solution:
Equation of the line passing through (3, 0) and (- 2, – 2) is
y – 0 = \(\frac{-2-0}{-2-3}\)(x – 3)
[Apply y – y1 = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)(x – x1)
= \(\frac{2}{5}\)(x – 3)
or 5y = 2x – 6 or 2x – 5y = 6.
If the point (8, 2) lies on it, (8, 2) will satisfy the equation of the line.
∴ 2 × 8 – 5 × 2
= 16 – 10 = 6.
Hence, (8, 2) lies on it.
Thus, (3, 0), (- 2, – 2) and (8, 2) are collinear.