Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.1
Question 1.
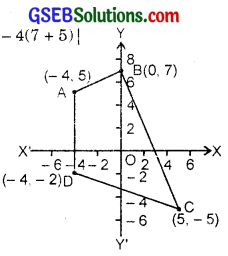
Draw a quadrilateral in the cartesian plane, whose vertices are (- 4, 5), (0, 7), (5, – 5) and (- 4, – 2). Also, find its area?
Solution:
Given points (- 4, 5), (0, 7), (5, – 5) and (-4, -2) are plotted. They are denoted by A, B, C and D respectively.
Now divide the quadrilateral into two triangles viz. ∆ABD and ∆BCD.
Area of a triangle = \(\frac{1}{2}\) |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)
The vertices of ∆ABD are (- 4, 5), (0, 7) and (- 4, – 2).
∴ Area of ∆ ABD = \(\frac{1}{2}\) |- 4(7 + 2) + 0(- 2 – 5) + (- 4)(5 – 7)|
= \(\frac{1}{2}\) |- 36 + 8| = \(\frac{28}{2}\) = 14 ……………… (1)
The vertices of ∆ BCD are (0, 7), (5, – 5) and (- 4, – 2).
∴ Area of ∆ BCD
= \(\frac{1}{2}\) |0(- 5 + 2) + 5(- 2 – 7) – 4(7 + 5)|
= \(\frac{1}{2}\) |- 45 – 48| = \(\frac{93}{2}\) ………………….. (2)
∴ Area of quadrilateral ABCD = Area of ∆ ABD + Area of ∆ BCD
= 14 + \(\frac{93}{2}\) [From (1) and (2)]
= \(\frac{28+93}{2}\) = \(\frac{121}{2}\) = 60.5 sq units.
Area Under Curve Calculator solves the input function and gives the output in the blink of an eye.
![]()
Question 2.
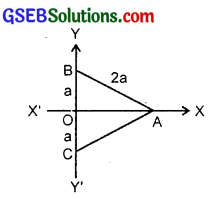
The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle.
Solution:
BC is the base of ∆ ABC such that BO = OC = a.
and AB = AC = 2a
Now, AO2 = AB2 – BO2
∴ AO = \(\sqrt{4 a^{2}-a^{2}}\) = \(\sqrt{3}\)a.
∴ The point A lying on x-axis is (\(\sqrt{3}\)a, 0).
The point B is (0, a) and the point C is (0, – a). When A lies on the left of y-axis, the vertices of triangle are (- \(\sqrt{3}\)a, 0), (0, a) and (0, – a)
Question 3.
Find the distance between P(x1, y1) and Q(x2, y2), when
(i) PQ is parallel to y-axis
(ii) PQ is parallel to x-axis.
Solution:
(i) When PQ is parallel toy-axis, every point on this line has the same abscissa. Let x2 = x1
∴ The points P and Q are P(x1, y1), Q(x1, y2)
∴ PQ = |y2 – y1|.
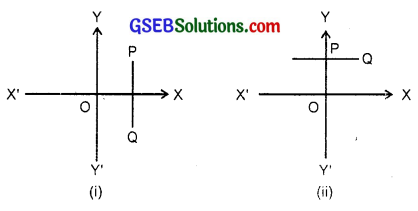
(ii) When PQ is parallel to x-axis. Every point on the line has the same ordinate. Let y2 = y1
∴ The coordinates of points P and Q are P(x1, y1), P(x2, y1)
∴ PQ = |x2 – x1|.
![]()
Question 4.
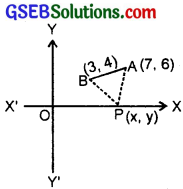
Find a point on the x-axis which is equidistant from the points (7, 6) and (3, 4).
Solution:
Let the point on the x-axis be (x1, 0).
The other two points A and B are A(7, 6) and B(3, 4).
W6 have: PA = PB or PA2 = PB2
or (x1 – 7)2 + 62 = (x1 – 32 + 42.
or x12 – 14x1 + 49 + 36 = x12 – 6x1 + 9 + 16
or – 14x1 + 85 = – 6x1 + 25.
or 8x1 = 60.
∴ x1 = \(\frac{60}{8}\) = \(\frac{15}{2}\).
∴ The point P on x-axis, equidistant from A and B is (\(\frac{15}{2}\), 0).
Question 5.
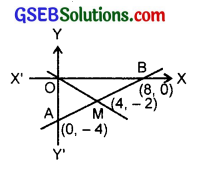
Find the slope of a line which passes through the origin and mid-point of the line segment joining the points P(0, – 4) and B(8, 0).
Solution:
Coordinates of mid-point of two points (x1, y1) and (x2, y2) are (\(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\)).
The mid-point A(0, – 4) and B(8, 0) is (\(\frac{8+0}{2}\), \(\frac{0-4}{2}\)) i.e; (4, – 2).
∴ The slope of line joining the points (x1, y1) and (x2, y2)
= \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
Here, the two points are O(0, 0) and M(4, – 2).
∴ Slope = \(\frac{-2-0}{4-0}\) = – \(\frac{1}{2}\).
![]()
Question 6.
Without using the pythagoras theorem, show that the points (4, 4), (3, 5) and (- 1, – 1) are the vertices of a right angled traingle.
Solution:
We have three points A(4, 4), B(3, 5) and C(- 1, – 1).
∴ Slope of AB = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)

= \(\frac{5-4}{3-4}\) = \(\frac{1}{-1}\) = – 1.
Slope of AC = \(\frac{-1-4}{-1-4}\) = \(\frac{-5}{-5}\) = 1.
Product of slopes of AB and AC = 1 × (- 1) = – 1.
∴ AB ⊥ AC
Hence, ∆ ABC is a right angled triangled.
Question 7.
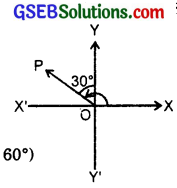
Find the slope of the line which makes an angle of 30° with the positive direction of y-axis (measured anticlockwise).
Solution:
The line OP makes an angle of 30° with y-axis measured anti-clockwise.
∴ OP makes an angle of 90° + 30°
= 120° with positive direction of x-axis.
∴ Slope of OP = tan 120° = tan (180° – 60°)
= – tan 60° = – \(\sqrt{3}\).
![]()
Question 8.
Find the value of x for which the points (x, – 1), (2, 1) and (4, 5) are collinear.
Solution:
We have the points A(x, – 1), B(2, 1) and C(4, 5).
A, B and C are collinear, if the slope of AB = slope of BC.
Slope of AB = \(\frac{1+1}{2-x}\) = \(\frac{2}{2-x}\).
Slope of BC = \(\frac{5-1}{4-2}\) = \(\frac{4}{2}\) = 2.
∴ \(\frac{2}{2-x}\) = 2
∴ 2 – x = 1 ⇒ x = 1.
Question 9.
Without using distance formula, show that the points (- 2, 1), (4, 0), (3, 3) and (- 3, 2) are the vertices of a parallelogram.
Solution:
The given points are A(- 2, – 1), B(4, 0), C(3, 3) and D(- 3, 2).
Slope of AB = \(\frac{1}{4+2}\) = \(\frac{1}{6}\)
Slopw of DC = \(\frac{3-2}{3+3}\) = \(\frac{1}{6}\)

∴ Slope of AB = Slope of DC
⇒ AB || DC.
Slope of AD = \(\frac{2+1}{-3+2}\) = \(\frac{3}{-1}\)
Slope of BC = \(\frac{3-0}{3-4}\) = \(\frac{3}{-1}\)
∴ Slope of AD = Slope of BC.
⇒ AD || BC.
Hence, ABCD is a parallelogram.
![]()
Question 10.
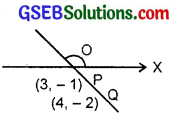
Find the angle between x-axis and the line joining the points (3, – 1) and (4, – 2).
Solution:
Slope of the line joining the points P(3, – 1) and Q(4, – 2)
= \(\frac{-2+1}{4-3}\) = \(\frac{-1}{1}\) = – 1.
⇒ tan θ = – 1 ⇒ θ = 135°.
So, required angle is 135°.
Question 11.
The slope of a line is double of the slope of another line. If tangent of the angle between them is \(\frac{1}{3}\), find the slopes of the lines?
Solution:
Let m1 and m2 be the slopes of the two lines.
Given that m1 = 2m2.
Let θ be the angle between the lines.
∴ tan θ = \(\frac{1}{3}\) = \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\).
Putting m1 = 2m2, we get
∴ \(\frac{1}{3}\) = \(\frac{2 m_{2}-m_{2}}{1+2 m_{2} \cdot m_{2}}\) = \(\frac{m_{2}}{1+2 m_{2}^{2}}\)
or 3m2 = 1 + 2m22 or 2m22 – 3m2 + 1 = 0.
or (2m2 – 1) × (m2 – 1) = 0
∴ m2 = 1 or \(\frac{1}{2}\)
m1 = 2m2.
∴ For m2 = 1, m1 = 2.
For m2 = \(\frac{1}{2}\), m1 = 2 × \(\frac{1}{2}\) = 1.
∴ Slopes of these lines are 1, \(\frac{1}{2}\) or 2, 1.
![]()
Question 12.
A line passes through the points (x1, y1) and (h, k). If the slope of the line is m, show that
k – y1 = m(h – x1).
Solution:
Slope of the line joining the points A(x1, y1) and B(h, k)
= \(\frac{k-y_{1}}{h-x_{1}}\) = m [Given]
∴ Cross multiplying, we get
k – y1 = m(h – x1).
Question 13.
If three points (h, 0), (a, b) and (0, k) lie on a line, show that \(\frac{a}{h}\) + \(\frac{b}{k}\) = 1.
Solution:
The given points are A(h, 0), B(a, b) and C(0, k).
They lie on the same line.
∴ Slope of AB = Slope of BC.
∴ Slope of AB = \(\frac{b-0}{a-h}\) = \(\frac{b}{a-h}\).
Slope of BC = \(\frac{k-b}{0-a}\) = \(\frac{k-b}{-a}\).
∴ \(\frac{b}{a-h}\) = \(\frac{k-b}{-a}\)
So, by cross multiplication, we get
– ab = (a – h)(k – b).
or – ab = ak – ab – hk + hb
or 0 = ak – hk + hb
or ak + hb = hk.
Dividing by hk, we get
\(\frac{ak}{hk}\) + \(\frac{hb}{hk}\) = 1
or \(\frac{a}{h}\) + \(\frac{b}{k}\) = 1.
![]()
Question 14.
Consider the following population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
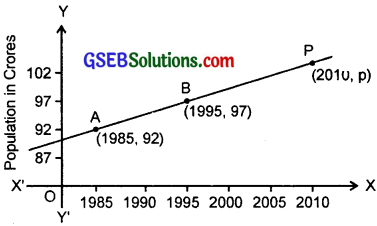
Solution:
Slope of the line joining the points A(1985, 92) and B(1995, 97)
= \(\frac{97-92}{1995-1985}\) = \(\frac{5}{10}\) = \(\frac{1}{2}\).
Let p be the population in the year 2010.
∴ The point P(2010, p) lies on it ⇒ Slope of BP = Slope of AB.
∴ Slope of BP = \(\frac{p-97}{2010-1995}\) = \(\frac{1}{2}\).
or 2(p – 27) = 2010 – 1995 = 15.
⇒ p – 97 = \(\frac{15}{2}\).
or p = 97 + 7.5 = 104.5 crores.