Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 10 Straight Lines Ex 10.3
Question 1.
Reduce the following equations into slope-intercept form and find their slopes and the intercept:
(i) x + 7y = 0
(ii) 6x + Sy – 5 = 0
(iii) y = 0
Solution:
(i) x + 7y = 0 or y = – \(\frac{1}{7}\)x + 0.
∴ Slope = – \(\frac{1}{7}\) and y-intercept = 0.
(ii) 6x + 3y – 5 = 0 or 3y = – 6x + 5
y = – 2x + \(\frac{5}{3}\).
∴ Slope = – 2 and y – intercept = \(\frac{5}{3}\).
(iii) y = 0 or y = 0x + 0.
∴ Slope = 0, y-intercept = 0.
![]()
Question 2.
Reduce the following equations into intercepts form and find their intercepts on the axes.
(i) 3x + 2y – 12 = 0
(ii) 4x – 3y = 6
(iii) 3y + 2 = 0
Solution:
(i) 3x + 2y – 12 = 0 or 3x + 2y = 12.
Dividing by 12, we get
\(\frac{x}{4}\) + \(\frac{y}{6}\) = 1.
∴ Intercepts on the axes are 4 and 6.
(ii) 4x – 3y = 6 or \(\frac{4}{6}\)x – \(\frac{y}{2}\) = 1.
or \(\frac{x}{3/2}\) + \(\frac{y}{-2}\) = 1.
Intercepts on the axes are \(\frac{3}{2}\) and – 2.
(iii) 3y + 2 = 0 or 3y = – 2.
or \(\frac{y}{-2/3}\) = 1 or \(\frac{x}{0}\) + \(\frac{y}{-2/3}\) = 1.
Intercepts on the axes are 0 and – \(\frac{2}{3}\).
Question 3.
Reduce the following equations into the normal form. Find their perpendicular distance from the origin and angle between perpendicular and positive direction of x-axis.
(i) x – \(\sqrt{3}\)y + 8 = 0
(ii) y – 2 = 0
(iii) x – y = 4
Solution:
(i) x – \(\sqrt{3}\)y + 8 = 0 or x – \(\sqrt{3}\)y = – 8.
or – x + \(\sqrt{3}\)y = 8.
Put rcos ω = – 1 and rsin ω = \(\sqrt{3}\).
Squaring and adding r2 = 1 + 3 = 4, ∴ r = 2.
cos ω = \(\frac{1}{2}\), sin ω = \(\frac{\sqrt{3}}{2}\) ∴ ω = 120° = \(\frac{2π}{3}\).
∴ xcos ω + y sin ω = \(\frac{8}{2}\) = 4.
∴ p = 4 and ω = \(\frac{2π}{3}\).
(ii) y – 2 = 0
Comparing it with Ax + By = C, we get
A = 0, B = 1, r = \(\sqrt{0+1^{2}}\) = 1.
∴ cos ω = 0, sin ω = \(\frac{8}{2}\) = 4.
∴ y = 2 ⇒ x cos \(\frac{π}{2}\) + ysin \(\frac{π}{2}\) = 2
∴ ω = \(\frac{π}{2}\), p = 2.
(iii) x – y = 4 ………………… (1)
Put r cos ω = 1, r sin ω = – 1.
So, r = \(\sqrt{1^{2}+(-1)^{2}}\) = \(\sqrt{2}\)
and cos ω = \(\frac{1}{\sqrt{2}}\), sin ω = \(\frac{1}{\sqrt{2}}\).
⇒ ω = 360° – 45° = 315°.
Dividing (1) by \(\sqrt{2}\), we get
\(\frac{1}{\sqrt{2}}\)x + (- \(\frac{1}{\sqrt{2}}\)y) = \(\frac{y}{\sqrt{2}}\) = 2\(\sqrt{2}\).
∴ Normal form of the given line is
xcos 315° + ysin 315° = 2\(\sqrt{2}\).
∴ ω = 315°, p = 2\(\sqrt{2}\).
![]()
Question 4.
Find the distance of the point (- 1, 1) from the line 12(x + 6) = 5(y – 2).
Solution:
The given line is
12(x + 6) = 5(y – 2)
or 12x + 72 = 5y – 10
or 12x – 5y + 72 + 10 = 0
or 12x – 5y + 82 = 0.
∴ The perpendicular distance from (x1, y1) to the line ax + by + c = 0 is \(\frac{\left(a x_{1}+b y_{1}+c\right)}{\sqrt{a^{2}+b^{2}}}\).
The point (x1, y1) is (- 1, 1).
∴ Perpendicular distances from (- 1, 1) to the line 12x – 5y + 82 = 0
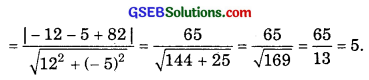
Question 5.
Find the points on the x-axis, whose distances from \(\frac{x}{3}\) + \(\frac{y}{4}\) = 1 are 4 units.
Solution:
The given line is \(\frac{x}{3}\) + \(\frac{y}{4}\) = 1.
Multiplying by 12, we get
4x + 3y = 12 or 4x + 3y – 12 = 0.
Any point on the x-axis is (x, 0).
∴ Perpendicular distance from (x, 0) to the given line
= \(\frac{|4 x-12|}{\sqrt{4^{2}+3^{2}}}\) = 4.
or \(\frac{|4 x-12|}{\sqrt{25}}\) = 4 or |4x – 12| = 5 × 4 = 20.
Taking (+ve) sign, 4x – 12 = 20 or 4x = 20 + 12 = 32
⇒ x = \(\frac{32}{4}\) = 8.
Taking (- ve) sign, 4x – 12 = – 20.
⇒ 4x = – 20 + 12 = – 8
∴ x = – 2.
∴ Required points on the x-axis are (8, 0) and (- 2, 0).
![]()
Question 6.
Find the distance between the parallel lines:
(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0.
(ii) l(x + y) + p = 0 and lx + ly – r = 0.
Solution:
One of the lines is
15x + 8y – 34 = 0.
Putting y = 0, 15x = 34 or x = \(\frac{34}{15}\).
∴ The point (\(\frac{34}{15}\), 0) lies on 15x + 8y – 34 = 0.
∴ Perpendicular distance from (\(\frac{34}{15}\), 0) to 15x + 8y + 31 = 0 is

Alternative method:
Perpendicular distance from the origin of these lines are p1 = \(\frac{-34}{\sqrt{15^{2}+8^{2}}}\) = \(\frac{- 34}{17}\) and p2 = \(\frac{31}{17}\).
∴ Perpendicular distance between the given parallel lines = |p2 – p1|
= |\(\frac{-34}{17}\) – \(\frac{31}{17}\)| = |\(\frac{-65}{17}\)| = \(\frac{65}{17}\).
(ii) The parallel lines are
l(x + y) + p = 0, lx + ly – r = 0.
Perpendicular distances from origin are
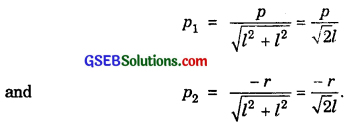
∴ Perpendicular distance between the given parallel lines are
|\(\frac{p}{\sqrt{2l}}\) – \(\frac{- r}{\sqrt{2l}}\)| = \(\frac{p+r}{\sqrt{2l}}\).
Question 7.
Find the equation of a line parallel to the line 3x – 4y + 2 = 0 and passing through the point (- 2, 3).
Solution:
The given line is 3x – 4y + 2 = 0.
∴ Slope of the line = \(\frac{3}{4}\).
∴ Slope of a parallel line = \(\frac{3}{4}\).
∴ The line passing through (- 2, 3) and parallel to 3x – 4y + 2 = 0 is
y – 3 = \(\frac{3}{4}\)(x + 2).
or 4y – 12 = 3x + 6
or 3x – 4y + 12 + 6 = 0 or 3x – 4y + 18 = 0.
Alternative Method.
Any line parallel to 3x – 4y + 2 = 0 is 3x – 4y = k.
[Note that the coeffs. of x and y are the same for parallel lines]
The line passes through (- 2, 3).
So, 3(- 2) – 4(3) = k
or k = – 6 – 12 = – 18
∴ Equation of the required line is 3x – 4y = – 18
or 3x – 4y + 18 = 0.

![]()
Question 8.
Find the equation of the line perpendicular to the line x – 7y + 5 = 0 and having x-intercept 3.
Solution:
The line having the x-intercept 3, passes through the point (3, 0).
The given line is x – 7y + 5 = 0.
∴ Slope of it = \(\frac{1}{7}\).
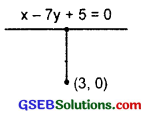
∴ Slope of perpendicular line = – 7.
∴ The line passing through (3, 0) and slope – 7 is
y – 0 = – 7(x – 3)
or y = – 7x + 21
∴ 7x + y – 21.
Alternative Method.
Any line perpendicular to ax + by + c = 0 is bx – ay + k – 0.
Note that here coefficients of x and y are interchanged and sign between them also changes from + to – and – to + in between.
∴ The line perpendicular to x – 7y + 5 = 0 is
7x + y = k.
Putting x = 3, y = 0 in it, we get 21 = k.
∴ Equation of the required line is
7x + y = 21.
Question 9.
Find the angles between the lines \(\sqrt{3x}\) + y = 1 and z + \(\sqrt{3}\)y = 1.
Solution:
The first line is \(\sqrt{3}\)x + y = 1 or y = – \(\sqrt{3x}\) + 1.
∴ The slope m1 = – \(\sqrt{3}\)
∴ m1 = – \(\sqrt{3}\).
The other line is x + \(\sqrt{3y}\) = 1.
or y = – \(\frac{1}{\sqrt{3}}\)x + \(\frac{1}{\sqrt{3}}\).
∴ The slope m2 of the line x + \(\sqrt{3y}\) = 1 is – \(\frac{1}{\sqrt{3}}\).
∴ m2 = – \(\frac{1}{\sqrt{3}}\).
If θ is the angle between two lines, then

So, acute angle between the lines is \(\frac{π}{6}\).
![]()
Question 10.
The line through the points (h, 3) and (4, 1) intersects the line 7x – 9y – 19 = 0 at right angles. Find the value of h?
Solution:
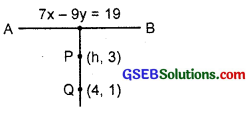
Slope of the line PQ passing through P(h, 3) and Q(4, 1).
= \(\frac{3-1}{h-4}\) = \(\frac{2}{h-4}\).
Slope of the line AB, i.e; 7x – 9y – 19 = 0 is \(\frac{7}{9}\).
The lines AB and PQ are perpendicular to each other.
∴ m1m2 = – 1 or \(\frac{2}{h-4}\) × \(\frac{7}{9}\) = – 1.
∴ 14 = – 9(h – 4) = – 9h + 36
∴ 9h = 36 – 14 = 22.
∴ h = \(\frac{22}{9}\).
Question 11.
Prove that the line through the point (x1, y1) and parallel to the line Ax + By + C = 0 is
A(x – x1) + B(y – y1) = 0.
Proof:
The given line is Ax + By + C = 0
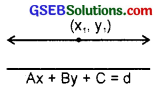
of y = – \(\frac{A}{B}\)x – \(\frac{C}{B}\)
∴ Slope of the parallel line = – \(\frac{A}{B}\)
The parallel line passes through (x1, y1) is
y – y1 = – \(\frac{A}{B}\)(x – x1)
or B(y – y1) = – A(x – x1)
or A(x – x1) + B(y – y1) = 0.
Alternatively. The line parallel to Ax + By + C = 0 is
Ax + By + k = 0 ………………. (1)
It passes through (x1y1)
∴ Ax1 + By1 + k = 0 ……………… (2)
Subtracting (2) from (1), we get
A(x – x1) + B(y – y1) = 0.
![]()
Question 12.
Two lines passing through the point (2, 3) intersects each other at an angle of 60°. If slope of one line is 2, find the equation of the other line.
Solution:
Let m be the slope of the other line.
Slope of one line = 2.
Angle between them = 60°.
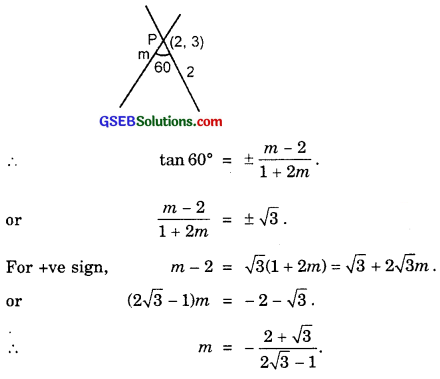
Equation of the line passing through P(2, 3) with slope
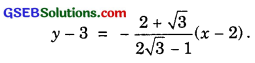
or (1 + 2\(\sqrt{3}\))y – 3(1 + 2\(\sqrt{3}\)) = (2 – \(\sqrt{3}\)x – 2(2 – \(\sqrt{3}\)).
or (1 + 2\(\sqrt{3}\))y – 3 – 6\(\sqrt{3}\) = (2 – \(\sqrt{3}\))x – 4 + 2\(\sqrt{3}\)
∴ (2 – \(\sqrt{3}\))x – (1 + 2\(\sqrt{3}\))y – 4 + 2\(\sqrt{3}\) + 3 + 6\(\sqrt{3}\) = 0.
or (2 – \(\sqrt{3}\))x – (1 + 2\(\sqrt{3}\))y – 1 + 8\(\sqrt{3}\) = 0.
∴ Required lines are
(\(\sqrt{3}\) + 2)x + (2\(\sqrt{3}\) – 1)y – 8\(\sqrt{3}\) – 1 = 0.
and (2 – \(\sqrt{3}\))x – (1 + 2\(\sqrt{3}\))y + 8\(\sqrt{3}\) – 1 = 0.
![]()
Question 13.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (- 1, 2).
Solution:
Slope of the line joining the points A(- 1, 2) and B(3, 4)
= \(\frac{4-2}{3+1}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\).

Right bisector PQ is perpendicular to AB.
∴ Slope of PQ = – 2.
Middle point of AB is (\(\frac{-1+3}{2}\), \(\frac{2+4}{2}\)), i.e; (1, 3).
Right bisector passes through M(1, 3).
∴ Equation of right bisector PQ is
y – 3 = – 2(x – 1) = – 2x + 2.
or 2x + y – 3 – 2 = 0
or 2x + y – 5 = 0.
Question 14.
Find the co-ordinates of the foot of the perpendicular from a point (- 1, 3) to the line 3ax – 4y – 16 = 0.
Solution:
The equation of the given line is 3x – Ay – 16 = 0.
The equation of a line perpendicular to the given line is
4x + 3y + k = 0, where k is a constant.
If this line passes through the point (- 1, 3), then
– 4 + 9 + k = 0 ⇒ k = – 5.
∴ The equation of the line passing through the point (- 1, 3) and perpendicular to the given line is
4x + 3y – 5 = 0.
∴ The required foot of the perpendicular is the point of intersection of the lines
3x – 4y – 16 = 0 …………… (1)
and 4x + 3y – 5 = 0 ……………….. (2)
Solving (1) and (2), by cross-multiplication, we have:
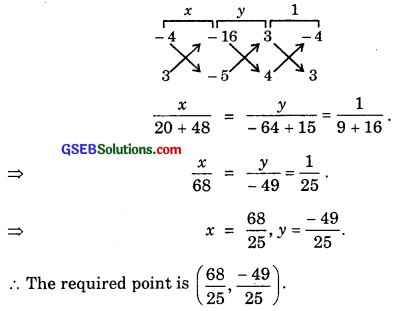
![]()
Question 15.
The perpendicular from the origin to the line y = mx + c meets it at the point (- 1, 2). Find the value of m and c.
Solution:
Let the perpendicular OM is drawn from the origin to AB. M is the foot of the perpendicular.
Slope of OM = \(\frac{2-0}{-1-0}\) = \(\frac{2}{-1}\).
Slope of AB = m
OM ⊥ AB.
∴ m × (- 2) = – 1
∴ m = \(\frac{1}{2}\).
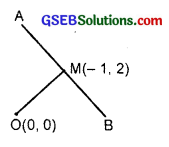
M(- 1, 2) lies on y = mx + c or y = \(\frac{1}{2}\)x + c.
∴ 2 = \(\frac{1}{2}\) × (- 1) + c, c = 2 + \(\frac{1}{2}\) = \(\frac{5}{2}\).
∴ m = \(\frac{1}{2}\) and c = \(\frac{5}{2}\).
Question 16.
If p and q are the lengths of perpendiculars from the origin to the lines xcos θ – ysin θ = kcos 2θ and x sec θ + y cosec θ = k respectively, prove that p2 + 4q2 = k2.
Solution:
The perpendicular distance from the origin to the line xcos θ – ysin θ = kcos 2θ ………………. (1)
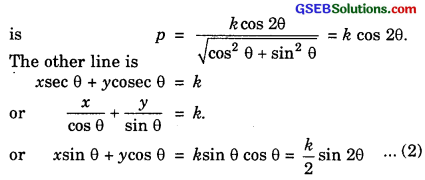
∴ The perpendicular distance q from the origin to the line (2) is

![]()
Question 17.
In the triangle ABC with vertices A(2, 3), B(4, – 1) and C(1, 2), find the equation and length of altitude from the vertex A.
Solution:
The vertices of ∆ ABC are A(2, 3), B(4, – 1) and C(1, 2) and AM is the altitude.
Slope of BC = \(\frac{2+1}{1-4}\) = \(\frac{3}{-3}\) = – 1.
∴ Slope of altitude AM = 1. [∵ m1m2 = – 1]

Now, altitude passes through A(2, 3) and has the slope 1.
∴ Equation of AM is
y – 3 = 1(x – 2).
or x – y + 3 – 2 = 0
or y – x = 1.
Equation of BC passing through B(4, – 1) and C(1, 2) is
y + 1 = – (x – 4).
or x + y = 3
or x + y – 3 = 0.
∴ Length of altitude = AM
= Perpendicular distance from A(2, 3) to BC
= \(\frac{2+3-3}{\sqrt{1^{2}+1^{2}}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
∴ Equation of altitude is y – x = 1 and length of altitude = \(\sqrt{2}\).
![]()
Question 18.
If p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that \(\frac{1}{p^{2}}\) = \(\frac{1}{a^{2}}\) + \(\frac{1}{b^{2}}\).
Solution:
Equation of the line which makes intercepts a and b on the axes is
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1.
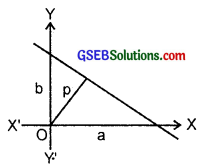
∴ The perpendicular distance p from the origin is given by
