Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 4 Principle of Mathematical Induction Ex 4.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 4 Principle of Mathematical Induction Ex 4.1
Prove the following by using the principle of mathematical induction for all n ∈ N?
1. 1 + 3 + 32 + … + 3n-1 = \(\frac{3^{n}-1}{2}\).
2. 13 + 23 + 33 + ………………. + n3 = (\(\frac{n(n+1)}{2}\)2.
3. 1 + \(\frac{1}{1+2}\) + \(\frac{1}{1+2+3}\) + ………….. + \(\frac{1}{1+2+3+………..+n}\) = \(\frac{2n}{n+1}\).
4. 1.2.3 + 2.3.4 + 3.4.5 + … + n(n + 1)(n + 2)
= \(\frac{n(n + 1)(n + 2)(n + 3)}{4}\).
5. 1.3 + 2.32 + 3.32 + ……………. + n.3n = \(\frac{(2 n-1) \cdot 3^{n+1}+3}{4}\)
6. 1.2 + 2.3 + 3.4 + ……………… + n(n + 1) = \(\frac{n(n + 1)(n + 2)}{3}\).
7. 1.3 + 3.5 + 5.7 + …………….. + (2n – 1)(2n + 1) = \(\frac{n\left(4 n^{2}+6 n-1\right)}{3}\).
8. 1.2 + 2.22 + 3.22 + …………….. + n.2n = (n – 1).2n+1 + 2.
9. \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{8}\) + ……………. + \(\frac{1}{2^{n}}\) = 1 – \(\frac{1}{2^{n}}\).
10. \(\frac{1}{2.5}\) + \(\frac{1}{5.8}\) + \(\frac{1}{8.11}\) + ………………. + \(\frac{1}{(3n – 1)(3n + 2)}\) = \(\frac{n}{6n + 4}\).
11. \(\frac{1}{1.2.3}\) + \(\frac{1}{2.3.4}\) + \(\frac{1}{3.4.5}\) + …………….. + \(\frac{1}{n(n + 1)(n + 2)}\) = \(\frac{n(n + 3)}{4(n + 1)(n + 2)}\).
12. a + ar + ar2 + …………… + arn-1 = \(\frac{a\left(1-r^{n}\right)}{1-r}\).
13. (1 + \(\frac{3}{1}\)) (1 + \(\frac{5}{4}\)) (1 + \(\frac{7}{9}\)) ……………. (1 + \(\frac{2 n+1}{n^{2}}\)) = (n + 1)2
14. (1 + \(\frac{1}{1}\)) (1 + \(\frac{1}{2}\)) (1 + \(\frac{1}{3}\)) …………….. (1 + \(\frac{1}{n}\)) = n + 1.
15. 12 + 32 + 52 + ………….. + (2n – 1)2 = \(\frac{n(2n – 1)(2n + 1)}{3}\).
16. \(\frac{1}{1.4}\) + \(\frac{1}{4.7}\) + \(\frac{1}{7.10}\) + …………….. + \(\frac{1}{(3n – 2)(3n + 1)}\) = \(\frac{n}{3n+1}\).
17. \(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + \(\frac{1}{7.9}\) + …………… + \(\frac{1}{(2n + 1)(2n + 3)}\) = \(\frac{n}{3(2n + 3)}\)
18. 1 + 2 + 3 + …………….. + n < \(\frac{1}{8}\) (2n + 1)2.
19. n(n + 1)(n + 5) is a multiple of 3.
20. 102n-1 + 1 is divisible by 11.
21. x2n – y2n is divisible by x + y.
22. 32n+2 – 8n – 9 is divisible by 8.
23. 41n – 14n is a multiple of 27.
24. (2n + 7) < (n + 3)2.
Solutions to Questions 1 – 24:
1. Let P(n) be the given statement
i.e. P(n) : 1 + 3 + 32 + ……………… + 3n-1 = \(\frac{3^{n}-1}{2}\).
Putting n = 1, P(1) = \(\frac{3 – 1}{2}\) = 1.
∴ P(n) is true for n = 1
Assume that P(k) is true.
So, P(k) : 1 + 3 + 32 + ……………. + 3k-1 = \(\frac{3^{k}-1}{2}\)
We shall prove that P(k + 1) is true whenever P(k) is true.
Adding 3k to both sides, we get
1 + 3 + 32 + ……………….. + 3k-1 + 3k = \(\frac{3^{k}-1}{2}\) + 3k

∴ P(k + 1) is also true whenever P(k) is true.
Hence, by principal of mathematical induction P(n) is true for all n ∈ N.
![]()
2. Let P(n) : 13 + 23 + 33 + ……………. + n3 = \(\frac{n^{2}(n+1)^{2}}{4}\).
For n = 1, L.H.S. = 13 = 1
and R.H.S. = \(\frac{1^{2}(1+1)^{2}}{4}\) = \(\frac{1×4}{4}\) = 1.
∴ L.H.S. = R.H.S., i.e; P(1) is true.
Let us suppose that P(k) is true,
∴ Putting n = k in (1), we have:
P(k) : 13 + 23 + 33 + ……………… + k3 = \(\frac{k^{2}(k+1)^{2}}{4}\) …………….. (2)
Adding (k + 1)3 to both sides, we get

Thus, P(n) is true for n = k + 1, i.e., P(k + 1) is true.
∴ By Principle of Mathematical Induction, P(n) is true for all natural numbers n.
3. Let P(n) : 1 + \(\frac{1}{1+2}\) + \(\frac{1}{1+2+3}\) + ………….. + \(\frac{1}{1+2+3+………….+n}\) = \(\frac{2n}{n+1}\) ………………. (1)
Putting n = 1, L.H.S. = 1, R.H.S. = \(\frac{2.1}{1+1}\) = \(\frac{2}{2}\) = 1.
L.H.S. = R.H.S. ∴ P(1) is true.
Let P(k) be true.
∴ Putting n = k, we get
P(k) : 1 + \(\frac{1}{1+2}\) + \(\frac{1}{1+2+3}\) + ………………. + \(\frac{1}{1+2+3+………….+k}\) = \(\frac{2k}{k+1}\)
Now we shall prove that P(k + 1) is true, whenever P(k) is true.
Adding \(\frac{1}{1 + 2 + 3 + ………….. + (k + 1)}\) to both sides, we get

∴ P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
4. Let P(n) : 1.2.3 + 2.3.4 + 3.4.5 + … + n(n + 1)(n + 2)
= \(\frac{n(n+1)(n+2)(n+3)}{4}\) ……………….. (1)
For n = 1, L.H.S. = 1.23 = 6
and R.H.S. = \(\frac{1(1 + 1)(1 + 2)(1 + 3)}{4}\) = \(\frac{1×2×3×4}{4}\) = 6.
∴ L.H.S. = R.H.S., i.e., P(1) is true.
∴ Putting n = k in (1), we have:
P(k) : 1.2.3 + 2.3.4 + 3.4.5 + …………… + k(k + 1)(k + 2) = \(\frac{k(k + 1)(k + 2)(k + 3)}{4}\) ……………. (2)
We assume that P(k) is true.
Adding (k + 1)(k + 2)(k + 3) to both sides of (2), we have:
1.2.3 + 2.3.4 + 3.4.5 + ………….. + k(k + 1)(k + 2) + (k + 1)(k + 2)(k + 3)

∴ P(n) is true for n = k + 1, i.e., P(k + 1) is true.
∴ By Principle of Mathematical Induction, P(n) is true for all natural numbers n.
5. Let P(n) : 1.3 + 2.32 + 3.33 + … + n.3n = \(\frac{(2 n-1) \cdot 3^{n+1}+3}{4}\)
Putting n = 1, L.H.S.= 1.3 = 3
and R.H.S. = \(\frac{(2-1) \cdot 3^{2}+3}{4}\) = \(\frac{12}{4}\) = 3.
∴ L.H.S. = R.H.S.
This shows that P(n) is true for n = 1.
Let P(n) be true for n = k.
∴ P(k) : 1.3 + 2.32 + 3.32 + ………… + k.3k = \(\frac{(12 k-1) \cdot 3^{k+1}+3}{4}\) is true. ………………. (1)
Adding (k + 1).3k+1 to both sides of (1), we get
L.H.S. = 1.3 + 2.32 + k.32 + … + k.3k + (k + 1).3k+1

This shows P(n) is true for n = k + 1.
i.e., P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction P(n) is true for all values of n ∈ N.
![]()
6. Let P(n) : 1.2 + 2.3 + 3.4 + ………….. + n(n + 1) = \(\frac{n(n+1)(n+2)}{3}\)
For n = 1, L.H.S. = 1.2 = 2
and R.H.S. = \(\frac{n(n + 1)(n + 2)}{3}\) = \(\frac{1.2.3}{3}\) = 1.2 = 2.
i.e., L.H.S. = R.H.S.
So, P(1) is true.
We assume that P(n) is true for n = k.
i.e., 1.2 + 2.3 + 3.4 + … + k(k + 1) = \(\frac{k(k + 1)(k + 2)}{3}\)
Last term in L.H.S. is k(k + 1)
Replacing k by k + 1, we get (k + 1)(k + 2)
Adding it to both sides, we get
L.H.S. = 1.2 + 2.3 + 3.4 + … + k(k + 1) + (k + 1)(k + 2)

Thus, P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all values of n ∈ N.
7. Let P(n) be the given statement.
i.e., P(n) = 1.3 + 3.5 + 5.7 + … + (2n – 1)(2n + 1)
= \(\frac{n\left(4 n^{2}+6 n-1\right)}{3}\)
Putting n = 1,
L.H.S. = 1.3 = 3
and R.H.S. = \(\frac{1 .\left(4.1^{2}+6.1-1\right)}{3}\) = \(\frac{4+6-1}{3}\) = \(\frac{9}{3}\) = 3.
L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Assume that P(n) is true for n = k, i.e., P(k) is true.
i.e., 1.3 + 3.5 + 3.7 + … + (2k – 1)(2k + 1) =\(\frac{k\left(4 k^{2}+6 k-1\right)}{3}\)
Last term in L.H.S. = (2k – 1)(2k + 1)
Replacing k by k + 1, we get
[2(k + 1) – 1][2(k + 1) + 1] = (2k + 1)(2k + 3)
Adding (2k + 1)(2k + 3) to both sides, we get
∴ L.H.S. = 1.3 + 3.5 + 5.7 + … + (2k – 1)(2k + 1) + (2k + 1)(2k + 3)

Thus, P(n) is true for n = k + 1.
∴ P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
8. Let P(n) be the given statement.
i.e., P(n) : 1.2 + 2.22 + 3.23 + … + n.2n = (n – 1)2n+1 + 2
Putting n = 1, L.H.S. = 1.2 = 2
and R.H.S. = 0 + 2 = 2.
∴ P(n) is true for n = 1.
Assume that P(n) is true for n = k, i.e., P(k) is true, i.e.,
1.2 + 2.3 + 3.4 + … + k.2k = (k – 1).2k+1 + 2
Last term in L.H.S. = k.2k.
Replacing k by k + 1, we get the next term = (k + 1).2k+1
Adding it to both sides, we get
L.H.S. = 1.2 + 2.22 + 3.23 + … + k.2k+1 + 1 + (k + 1).2k+1
and R.H.S. = (k – 1).2k+1 + 2 + (k + 1).2k+1
= 2k+1.[k – 1 + k + 1] + 2 = 2k.2k+1 + 2
= k.2k+2 + 2.
This proves P(n) is true for n = k + 1.
Thus, P(k + 1) is true, whenever P(k) is true.
∴ By principle of mathematical induction, P(k) is true for all n ∈ N.
![]()
9. Let P(n) be the given statement.
i.e., P(n): \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{8}\) + ………….. + \(\frac{1}{2^{n}}\) = 1 – \(\frac{1}{2^{n}}\).
Putting n = 1, L.H.S. = \(\frac{1}{2}\)
and R.H.S. = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\).
∴ P(n) is true for n = 1.
Suppose P(n) is true for n = k.
∴ \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{8}\) + …………… + \(\frac{1}{2^{k}}\) = 1 – \(\frac{1}{2^{k}}\)
Last term in L.H.S. = \(\frac{1}{2^{k}}\).
Replacing k by k + 1,
last term becomes \(\frac{1}{2^{k+1}}\).
Adding \(\frac{1}{2^{k+1}}\) to both sides, we get
L.H.S. = \(\frac{1}{2}\) + \(\frac{1}{4}\) + \(\frac{1}{8}\) + ……………… + \(\frac{1}{2^{k}}\) + \(\frac{1}{2^{k+1}}\)
and R.H.S. = 1 – \(\frac{1}{2^{k}}\) + \(\frac{1}{2^{k+1}}\) = 1 – \(\frac{1}{2^{k}}\) (1 – \(\frac{1}{2}\))
= 1 – \(\frac{1}{2^{k}}\).\(\frac{1}{2}\) = 1 – \(\frac{1}{2^{k+1}}\).
This shows P(n) is true for n = k + 1.
Thus, P(k + 1) is true, whenever P(k) is true.
Thus, by principle of mathematical induction, P(n) is true for all n ∈N.
10. Let the given statement be P(n) i.e.,
P(n) : \(\frac{1}{2.5}\) + \(\frac{1}{5.8}\) + \(\frac{1}{8.11}\) + ………….. + \(\frac{1}{(3n – 1)(3n + 2)}\) = \(\frac{n}{6n + 4}\).
Putting n = 1, L.H.S. = \(\frac{1}{2.5}\) = \(\frac{1}{10}\)
and R.H.S. = \(\frac{1}{6 + 4}\) = \(\frac{1}{10}\).
∴ P(n) is true for n = 1.
Assuming P(n) is true for n = k, i.e., P(k) is true, i.e.,
\(\frac{1}{2.5}\) + \(\frac{1}{3.8}\) + \(\frac{1}{8.11}\) + ………… + \(\frac{1}{(3k – 1)(3k
+ 1)}\) = \(\frac{k}{6k + 4}\).
Now, kth term = \(\frac{1}{(3k – 1)(3k + 2)}\).
∴ (k + 1)th term = \(\frac{1}{[3(k + 1) – 1][3(k + 1) + 1]}\) = \(\frac{1}{(3k + 2)(3k + 5)}\).
Adding this term to both sides, we get
L.H.S. = \(\frac{1}{2.5}\) + \(\frac{1}{3.8}\) + \(\frac{1}{8.11}\) + ………………. + \(\frac{1}{(3k – 1)(3k + 2)}\) + \(\frac{1}{(3k + 2)(3k + 5)}\)
and R.H.S.

This shows that P(n) is true for n = k + 1.
∴ P(k + 1) is true, whenever P(k) is true. So, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
11. Let P(n) be the given statement, i.e.,
P(n) : \(\frac{1}{1.2.3}\) + \(\frac{1}{2.3.4}\) + \(\frac{1}{3.4.5}\) + ………….. + \(\frac{1}{n(n + 1)
(n + 2)}\) = \(\frac{n(n + 3)}{4(n + 1)(n + 2)}\).
Putting n = 1, L.H.S. = \(\frac{1}{1.2.3}\) = \(\frac{1}{6}\)
and R.H.S = \(\frac{1(1 + 3)}{4(1 + 1)(1 + 2)}\) = \(\frac{4}{4.2.3}\) = \(\frac{1}{6}\).
∴ P(n) is true for n = 1.
Assuming P(n) is true for n = k, i.e., P(k) is supposed to be true

Adding this term to both sides, we get

This shows P(n) is true for n = k + 1, i.e., P(k + 1) is true whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
12. Let P(n) : a + ar + ar2 + … + arn-1 = \(\frac{a\left(1-r^{n}\right)}{1-r}\), r ≠ 1 ………………. (1)
For n = 1, L.H.S. = a
and R.H.S. = \(\frac{a(1-r)}{1-r}\) = a.
∴ L.H.S. = R.H.S., i.e., P(1) is true.
Let us suppose that P(k) is true.
Putting n = k in (1), we have:
a + ar + ar2 + … + arn-1 = \(\frac{a\left(1-r^{n}\right)}{1-r}\) …………….. (2)
Adding ark to both sides of (2), we have:
a + ar + ar2 + ……………… + ark-1 + ark

∴ P(n) is true for n = k + 1, i.e., P(k + 1) is true.
Thus, P(k + 1) is true, whenever P(&) is true.
∴ By principle of mathematical induction, P(n) is true for all natural numbers n.
13. Let the given statement be denoted by P(n), i.e.,
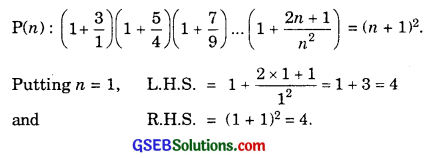
L.H.S. = R.H.S.
∴ P(n) is true for n = 1.
Suppose P(k) is true.

∴ P(n) is true for n = k + 1, i.e., P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
14. Let the given statement be P(n), i.e.,
P(n) : (1 + \(\frac{1}{1}\))(1 + \(\frac{1}{2}\))(1 + \(\frac{1}{3}\)) ……………. (1 + \(\frac{1}{n}\)) = n + 1.
For n = 1, L.H.S. = 1 + \(\frac{1}{1}\) = 2
and R.H.S. = 1 + 1 = 2.
∴ P(n) is true for n = 1.
Let P(&) be true, i.e.,
(1 + \(\frac{1}{1}\))(1 + \(\frac{1}{2}\))(1 + \(\frac{1}{3}\)) …………… (1 + \(\frac{1}{k}\)) = k + 1 is true.
Multiplying both sides by (1 + \(\frac{1}{k+1}\)), we get
L.H.S. = (1 + \(\frac{1}{1}\))(1 + \(\frac{1}{2}\))(1 + \(\frac{1}{3}\)) ………………. (1 + \(\frac{1}{k}\))(1 + \(\frac{1}{k+1)}\)
and R.H.S = (k + 1) (1 + \(\frac{1}{k + 1}\) = (k + 1)(\(\frac{k+1+1)}{k+1}\) = (k + 2)
= (\(\sqrt{k+1}\) + 1)
Therefore P(k + 1) is also true, whenever P(k) is true. Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
15. Let the given statement be P(n), i.e.,
P(n) : 12 + 32 + 52 + … + (2n – 1)2 = \(\frac{n(2n – 1)(2n + 1)}{3}\).
For n = 1, L.H.S. = 12 = 1
and R.H.S. = \(\frac{1.(2 – 1)(2 + 1)}{3}\) = \(\frac{1.1.3}{3}\) = 1.
∴ P(n) is true for n – 1.
Suppose P(&) is true for n = k i.e.,
12 + 32 + 52 + …………… + (2k – 1)2 = \(\frac{k(2k – 1)(2k + 1)}{3}\).
Adding (2k + 1)2 to both sides, we get
L.H.S. = 12 + 32 + 52 + ……………. + (2k – 1)2 + (2k + 1)2

Thus, P(k + 1) is true.
∴ P(k + 1) is true, whenever P(k) is true.
∴ By principle of mathematical induction, Pin) is true for all values of n ∈ N.
![]()
16. Let the given statement be P(n), i.e.,
P(n) : \(\frac{1}{1.4}\) + \(\frac{1}{4.7}\) + \(\frac{1}{7.10}\) + …………….. + \(\frac{1}{(3n – 2)(3n + 1)}\) = \(\frac{n}{3n + 1}\).
For n = 1, L.H.S. = \(\frac{1}{1.4}\) = \(\frac{1}{4}\)
and R.H.S. = \(\frac{1}{3.1+1}\) = \(\frac{1}{4}\).
∴ P(n) is true for n = 1.
Assuming P(k) is true for some value of n = k.
∴ \(\frac{1}{1.4}\) + \(\frac{1}{4.7}\) + \(\frac{1}{7.10}\) + ………………. + \(\frac{1}{(3k – 2)(3k + 1)}\) = \(\frac{k}{3k + 1}\).
Adding \(\frac{1}{(3k + 1)(3k + 2)}\) both sides, we get

Therefore, P(k + 1) is true for n = k + 1, i.e., P(k + 1) is true, whenever P(k) is true. Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
17. Let P(n) be the given statement, i.e.,
P(n) : \(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + \(\frac{1}{7.9}\) + …………….. + \(\frac{1}{(2n + 1)(2n + 3)}\) = \(\frac{n}{3(2n + 3)}\).
For n = 1, L.H.S. = \(\frac{1}{3.5}\) = \(\frac{1}{15}\)
and R.H.S. = \(\frac{1}{3.(2 + 3)}\) = \(\frac{1}{3.5}\) = \(\frac{1}{15}\).
Thus, P(x) is true for n = 1.
Suppose P(k) be true for n = k, i.e.,
\(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + \(\frac{1}{7.9}\) + ………….. + \(\frac{1}{(2k + 1)(2k + 3)}\) = \(\frac{k}{3(2k + 3)}\).
Adding \(\frac{1}{2(k + 3)(2k + 5)}\) to both sides, we get
L.H.S. = \(\frac{1}{3.5}\) + \(\frac{1}{5.7}\) + \(\frac{1}{7.9}\) + ……………. + \(\frac{1}{(2k + 1)(2k + 3)}\) + \(\frac{1}{(2k + 3)(2k + 5)}\)

Hence, P(k + 1) is true for n = k + 1, i.e., P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
18. Let P(n) : 1 + 2 + 3 + …………. + n < \(\frac{1}{8}\) (2n + 1)2 ………………. (1)
For n = 1, (1) becomes 1 < \(\frac{1}{8}\) (2 + 1)2 ⇒ 1 < \(\frac{9}{8}\) ⇒ 1 < 1 \(\frac{1}{8}\)
which is true, i.e., P(1) is true.
Let us suppose that P(k) is true.
∴ Putting n = k in (1), we have:
1 + 2 + 3 + ………….. + k < \(\frac{1}{8}\) (2k + 1)2
Adding (k + 1) to both sides of (2), we have:

⇒ 1 + 2 + 3 + …………… + k + (k + 1) < \(\frac{1}{8}\) (4k2 + 12k + 9)
⇒ 1 + 2 + 3 + ……………… + k + (k + 1) < \(\frac{1}{8}\) (2k + 3)2
⇒ 1 + 2 + 3 + ……………. + k + (k + 1) < \(\frac{1}{8}\) [2(k + 1) + 1]2 ……………… (3)
∴ P(k + 1) is true.
∴ By principle of mathematical induction, P(n) is true for all natural numbers n.
19. Let the statement be denoted by P(n), i.e.,
P(n) : n(n + 1)(n + 5) is a multiple of 3.
For n = 1, n(n + 1 )(n + 5) = 1.2.6 = 12 = 3.4.
P(n) is true for n = 1.
Suppose P(k) is true for n = k i.e.
k(k + 1)(k + 5) = 3m (say)
or k3 + 6k2 + 5k = 3m …………………… (1)
Replacing k by k + 1 in L.H.S. of (1), we get
(k + 1)(k + 2)(k + 6) = k(k2 + 8k + 12) + (k2 + 8k + 12)
= k3 + 9k2 + 20k + 12
= (k3 + 6k2 + 5k) + (3k2 – 15k + 12)
= 3m + 3k2 + 15k + 12 [From (1)]
= 3(m + k2 + 5k + 4).
i.e., (k + 1)(k + 2)(k + 6) is a multiple of 3, i.e.,
P(k + 1) is a multiple of 3, if P(k) is a multiple of 3.
i.e., P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
20. Let P(n) : 10(2n – 1) + 1 is divisible by 11 for every natural number n.
For n = 1, P(1) = 102-1 + 1 = 10 + 1 = 11,
which is divisible by 11
∴ P(1) is true.
Put n = k in (1), we have:
102k-1 + 1 is divisible by 11.
∴ 102k-1 + 1 = 11m, for some integer m.
⇒ 102k-1 = 11m – 1 …………………. (1)
Putting n = k + 1(k + 1) in 102n-1 + 1, it becomes
102(k+1)-1 + 1 = 102k+1 + 1 = 102k-1 = 102 + 1
= 100.102k-1 + 1 = 100(11m – 1) + 1 [Using (1)]
= 100 × 11m – 100 + 1
= 100 × 11m – 99
= 11(100m – 9), which is divisible by 11. [∵ 11 is a factor of R.H.S]
∴ 102(k+1)-1 + 1 is divisible by 11.
∴ P(n) is true for n = k + 1, i.e; P(k + 1) is true.
∴ By principle of mathematical induction, P(n) is true for all natural numbers n.
21. Let the statement be P(n), i.e.,
P (n) : x2n – y2n is divisible by x + y. ………………. (1)
Putting n = 1, x2n – y2n = x2 – y2 = (x + y)(x – y),
which is divisible by x + y.
⇒ P(n) is true for n = 1.
Let P(k) be true, i.e,
x2k – y2k is divisible by x + y
or x2k – y2k = m(x + y).
or x2k = m(x + y) + y2k ………………… (2)
Replace k by k + 1 in x2k from (2), we get
x2(k + 1) – y2(k + 1) = x2k+2 – y2k+2
= x2.x2k – y2k+2.
Putting the value of x2k from (2), we get
x2(k + 1) – y2(k + 1) = x2[m (x + y) + y2k] – y2k + 2
= m(x + y)x2 + x2y2k – y2k + 2
= m(x + y)2 + y2k)(x2 – y2)
= m(x + y)x2 + (x + y)(x – y)y2k
Therefore x2(k+1) – y2(k + 1) is divisible by (x + y).
i.e., P(k + 1) is true whenever P(k) is true.
By principle of mathematical induction, P(n) is true for all n ∈ N.
![]()
22. Let the statement be denoted by P(n), i.e;
P(n) : 32n+2 – 8n – 9 is divisible by 8.
For n = 1, 32n+2 – 8n – 9 = 32+2 – 8.1 – 9
= 34 – 8 – 9 = 81 – 17 = 64,
which is divisible by 8.
Let P(k) be the true statement for some value of n = k.
∴ 32k+2 – 8k – 9 is divisible by 8.
or 32k+2 – 8k – 9 = 32(k + 1) + 2 – 8(k + 1) – 9
= 32k + 2 + 2 – 8k – 8 – 9
= 32. 32k+2 – 8k – 17
= 9.32k+2 – 8k – 17.
Putting the value of 32k+2 from (1), we get
22k+4 – 8k – 17 = 9(8m + 8k + 9) – 8k – 17
= 72m + 72k + 81 – 8k – 17
= 72m + 64k + 64
= 8(9m + 8k + 8)
Hence, 32k+4 – 8(k + 1) – 9 is divisible by 8.
i.e; P(k + 1) is true, whenever P(k) is true.
Hence, by principle of mathematical induction, P(n) is true for all n ∈ N.
23. Let P(n) be the given statement, i.e;
P(n) : 41n – 14n is a multiple of 27.
For n = 1, 41n – 14n = 41 – 14 = 27.
∴ P(n) is true for n = 1.
Let P(k) be true for some value of n = k.
P(k) : 41k – 14k = 27m, where m is a positive integer.
41k = 27 + 14k ……………… (1)
Replacing k by k + 1 in L.H.S. of (1), we get
41k + 1 – 14k + 1 = 41.41k – 14k + 1
= 41. (27m + 14k) – 14k + 1 [From (1)]
= 27.41 m + 14k(41 – 14)
= 27. 41m + 14k.27
= 27[41m + 14k]
This shows 41k + 1 – 14k + 1 is a multiple of 27.
or P(k + 1) is true, whenever P(k) is true.
Hence, by principal of mathematical induction, P(n) is true for all n ∈ N.
![]()
24. Let P(n) : (2n + 7) < (n + 3)2 ………………. (1)
For n = 1, (1) becomes 2 × 1 + 7 < (1 + 3)2 ⇒ 9 < 16, which is true.
∴ P(1) is true
Let us suppose that P(k) is true.
∴ Putting n = k in (1), we have:
2(k + 7) < (k + 3)2 ………………….. (2)
Now, we will prove that P(k + 1) is true.
i.e; 2(k + 1) + 7 < (k + 4)2.
We know that 2k + 7 < (k + 3)2.
⇒ 2k + 7 + 2 < (k + 3)2 + 2 [Adding 2 t0 both sides]
⇒ 2(k + 1) + 7 < (k + 3)2 + 2 ……………… (3)
⇒ 2 (k + 1) + 7 < k2 + 6k + 11
Adding 2k + 5 to R.H.S., we get
⇒ 2(k + 1) + 7 < x2 + 7k + 16
or 2(k + 1) + 7 < (k + 4)2.
Thus, P(k + 1) is true. Hence, P(n) is true for n = k + 1.
∴ By principal of mathematical induction, P(n) is true for all natural numbers n.