Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Miscellaneous Exercise Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Maths Chapter 3 Trigonometric Functions Miscellaneous Exercise
1. 2cos \(\frac{π}{13}\)cos \(\frac{9π}{13}\) + cos \(\frac{3π}{13}\) + cos \(\frac{5π}{13}\) = 0
2. (sin 3x + sin x)sin x + (cos 3x – cos x)cos x = 0
3. (cos x + cos y)2 + (sin x – sin y)2 = 4 cos2 \(\frac{x+y}{2}\)
4. (cos x – cos y)2 + (sin x – sin y)2 = 4 sin2 \(\frac{x-y}{2}\)
Solutions to questions 1 – 4:
1. L.H.S. = 2 cos \(\frac{π}{13}\)cos \(\frac{9π}{13}\) + cos \(\frac{3π}{13}\) + cos \(\frac{5π}{13}\)
= cos \(\frac{10π}{13}\) + cos \(\frac{8π}{13}\) + cos \(\frac{3π}{13}\) + cos \(\frac{5π}{13}\)
[∵ 2cos A cos B = cos (A + B) + cos (A – B)]

= 0 = R.H.S.
2. L.H.S. = (sin 3x + sinx)sinx + (cos3x – cosx)cosx
= sin3xsinx + sin2x + cos3x cosx – cos2x
= (cos 3x cos x + sin 3x sin x) – (cos2x – sin2 x)
= cos (3x – x) – cos 2x + cos2x = cos 2x – cos 2x = 0
= R.H.S.
3. L.H.S. = (cos x + cos y)2 + (sin x – sin y)2

4. L.H.S. = (cos x – cos y)2 + (sin x – sin y)2
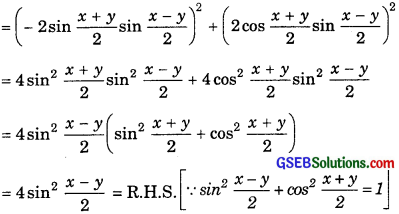
![]()
Prove that:
5. sin x + sin 3x + sin 5x + sin 7x = 4cos x cos 2x sin 4x
6. \(\frac{(sin 7x + sin 5x) + (sin 9x + sin 3x)}{(cos 7x + cos 5x) + (cos 9x + cos 3x)}\) = tan 6x
7. sin 3x + sin 2x – sin x = 4sin x cos \(\frac{x}{2}\) cos \(\frac{3x}{2}\)
solutions:
5. L.H.S. = sin x + sin 3x + sin 5x + sin 7x
= (sin 7x + sin x) + (sin 5x + sin 3x)
= 2sin \(\frac{7x + x}{2}\)cos \(\frac{7x – x}{2}\) + 2sin \(\frac{5x + 3x}{2}\)cos \(\frac{5x – 3x}{2}\)
= 2sin 4x cos 3x + 2 + 2 sin 4x cos x
= 2sin 4x[cos 3x + cos x]
= 2sin 4x. 2cos \(\frac{3x+x}{2}\)cos \(\frac{3x-x}{2}\)
= 4 sin 4x. cos 2x. cos x
= 4cos x cos 2x. sin 4x = R.H.S.
6. L.H.S. =
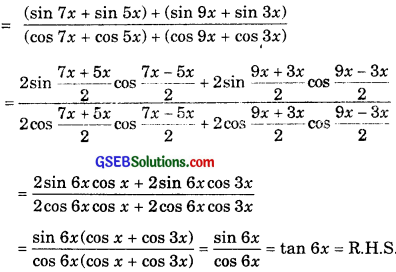
7. L.H.S. = sin 3x + (sin 2x – sin x)
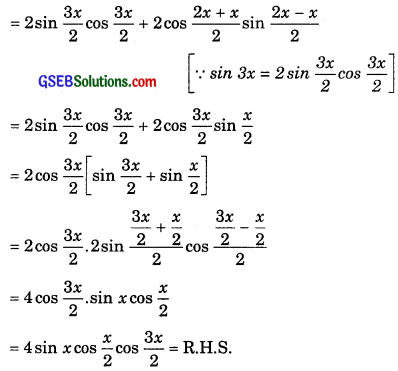
Find sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) in each of the following problems:
8. tan x = – \(\frac{4}{3}\), x in quadrant II.
9. cos x = – \(\frac{1}{3}\), x in quadrant III.
10. sin x = \(\frac{1}{4}\), x in quadrant II.
Solutions to questions (8 – 10):
8. since x lies in the second quadrant, therefore cos x is negative.
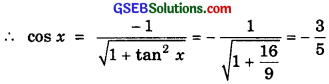
Now x, lies in 2nd quadrant
⇒ \(\frac{π}{2}\) < x < π ⇒ \(\frac{π}{4}\) < \(\frac{x}{2}\) < \(\frac{π}{2}\)
⇒ \(\frac{x}{2}\) lies in first quadrant.
⇒ sin \(\frac{x}{2}\), cos \(\frac{x}{2}\) and tan \(\frac{x}{2}\) are positive.

Since x lies in quadrant III, therefore
180° < x < 270°
⇒ 90° < \(\frac{x}{2}\) < 135°
or \(\frac{x}{2}\) lies in quadrant II.

Since x lies in quadrant II, therefore
cos x < 0.

But x lies in quadrant II.

But cos \(\frac{x}{2}\) > 0 for 45° ≤ \(\frac{x}{2}\) ≤ 90°

= 4 + \(\sqrt{15}\).