GSEB Solutions Class 11 Maths Chapter 9 Sequences and Series Ex 9.2

Gujarat Board GSEB Textbook Solutions Class 11 Maths Chapter 9 Sequences and Series Ex 9.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Maths Chapter 9 Sequences and Series Ex 9.2

Question 1.
Find the sum of odd integers from 1 to 2001.
Solution:
We have to find the sum 1 + 3 + 5 + ………….. + 2001.
Let the nth term be the last term.
∴ a + (n – 1)d = 2001.
Here, a = 1, d = 2.
∴ 1 + [n – 1].2 = 2001 or 2[n – 1] = 2000 – 1 = 2000
∴ n – 1 = 2000, n = 1001
∴ Sum = \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{1001}{2}\)[2.1 + (1001 – 1) × 2]
= \(\frac{1001}{2}\) × 2[1 + 100 – 1] = 1001 × 1001
= 1002001.

Question 2.
Find the sum of all natural numbers lying between 100 and 1000 which are multiples of 5?
Solution:
We have to find the sum 105 + 110 + 115 + … 995
Let 995 = nth term.
∴ a + (n – 1)d = 995.
n = 199 – 20 = 179
∴ 105 + 110 + 115 + ……….. + 995 = \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{179}{2}\) [2 × 105 + (179 – 1) × 5]
= \(\frac{179}{2}\) [2 × 105 + 5 × 178]
= 179(105 + 5 × 89)
= 179(105 + 445) = 179 × 550
= 98450.

Question 3.
In an A.P., the first term is 2 and the sum of first five terms is one-fourth of the sum of next five terms. Show that its 20th term is – 112.
Solution:
Let d be the common difference.
∴ Sum of first 5 terms = \(\frac{n}{2}\) [(2a + (n – 1))d]
= \(\frac{5}{2}\) [2 × 2 + (5 – 1)d]
= \(\frac{5}{2}\)[4 + 4d] = 5(2 + 2d).
6^thterm = a + (6 – 1)d = a + 5d.
∴ (a + 5d) + (a + 6d) + ………….. to 5 terms
= \(\frac{5}{2}\) [2(a + 5d) + (5 – 1)d]
= \(\frac{5}{2}\) [2a + 10d + 4d]
= \(\frac{5}{2}\) [2a + 14d] = 5(a + 7d)
= 5(2 + 7d)
Sum of first five terms = \(\frac{1}{4}\) × sum of next 5 terms
5(2 + 2d) = \(\frac{1}{4}\) × 5(2 + 7d)
or 4(2 + 2d) = 2 + 7d
∴ d = – 6
∴ T₂₀ = a + (20 – 1)d = 2 + 19 × (- 6)
= 2 + (- 114) = – 112.

4. How many terms of the A.P. – 6, – \(\frac{11}{2}\), – 5, ……………… are needed to give the sum – 25?
Solution:
Here, a = – 6, d = – \(\frac{11}{2}\) – (- 6) = \(\frac{- 11}{2}\), – 5, …………….. are needed to give the sum – 25?
Solution:
Here, a = – 6, d = – \(\frac{11}{2}\) – (- 6) = \(\frac{- 11}{2}\) + 6 = \(\frac{- 11+12}{2}\) = \(\frac{1}{2}\).
Let n be the number of terms, so that
S_n = – 25.
Since S_n = \(\frac{n}{2}\)[2a + (n – 1)d], we have:

⇒ – 100 = n(n – 25)
⇒ n² – 25n + 100 = 0
⇒ (n – 5)(n – 20) = 0
⇒ n = 5 or n = 20.
Both values of n give the required sum.

Question 5.
In an A.P., if the pth term is \(\frac{1}{q}\) and the qth term is \(\frac{1}{p}\), prove that the sum of first pq terms is \(\frac{1}{2}\)(pq + 1), where p ≠ q?
Solution:
Let a be the first term and d be the common difference of £he A.P. Then,

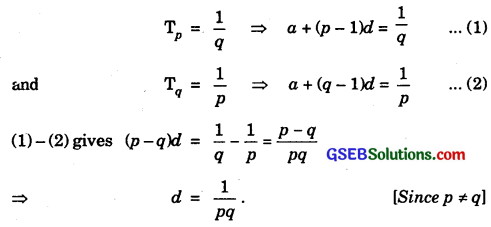
Putting d = \(\frac{1}{pq}\) in (1), we get

Question 6.
If the sum of a certain number of terms of the A.P; 25, 22, 19, ………………. is 116. Find the last term?
Solution:
a = 25, d = 22 – 25 = – 3. Let n be the number of terms.
Sum = 116.
Now, sum = \(\frac{n}{2}\) [2a + (n – 1)d]
∴ 116 = \(\frac{n}{2}\) [50 + (n – 1)(- 3)]
or 232 = n[50 – 3n + 3] = n[53 – 3n]
= – 3n² + 53n.
⇒ 3n² – 53n + 232 = 0.
⇒ (n – 8)(3n – 29) = 0.
∴ n = 8 or \(\frac{29}{3}\). But n ≠ \(\frac{29}{3}\).
∴ n = 8.
Now, T₈ = a + (8 – 1)d = 25 + 7 × (- 3)
= 25 – 21 = 4.
∴ Last term = 4.

Question 7.
Find the sum to n terms of an A.P., whose kth term is 5k + 1.
Solution:
T_k = 5k + 1.
Putting k = 1 and 2, we get
T₁ = 5 × 1 + 1 = 5 + 1 = 6
and T₂ = 5 × 2 + 1 = 10 + 1 = 11.
∴ d = T₂ – T₁ = 11 – 6 = 5.
Here, a = 6, d = 5.
Sum of n terms = \(\frac{n}{2}\)[2a + (n – 1)d].
= \(\frac{n}{2}\)[2 × 6 + (n – 1) × 5]
= \(\frac{n}{2}\)[12 + 5n – 5]
= \(\frac{n(5n+7)}{2}\).

Question 8.
If the sum to n terms of an A.P. is (pn + qn²), where p and q are constants, find the common difference?
Solution:
Let S_n be the sum to n terms.
∴ S_n = pn + qn²
Putting n = 1 and 2, we get
S₁ = T₁ = p.1 + q.1² = p + q
and S₂ = T₁ + T₂ = p.2 + q.2² = 2p + 4q.
T₂ = (T₁ + T₂) – T₁ = S₂ – S₁
= [(2p + 4q)] – (p + q)]
= p + 3q.
∴ d = T₂ – T₁ = (p + 3q) – (p + q) = 2q.
∴ Common differences of the A.P. is 2q.

Question 9.
The sums of first n terms of two arithmetic progressions are in the ratio (5n + 4) : (9n + 6). Find the ratio of their 18th terms?
Solution:
Let a₁ and d₁ be the first term and common difference of the first A.P. and a₂ and d₂ be the first term and common difference of the second A.P.
If S₁ and S₂ be their sums respectively, then

Multiplying numerator and denominator by 2, we get

Question 10.
If the sum of first p terms of an A.P. is equal to the sum of first q terms, then find the sum of first (p + q) terms?
Solution:
Let a be the first term and d be the common difference of A.P.
∴ Sum of first p terms = \(\frac{p}{2}\)[2a + (p – 1)d] ……………. (1)
and sum of first q terms = \(\frac{q}{2}\)[2a + (q – 1)d] …………….. (2)
Equating (1) and (2), we get
\(\frac{p}{2}\)[(2a + (p – 1)d] = \(\frac{q}{2}\)[2a + (q – 1)d].
Transposing the terms of R.H.S. to L.H.S., we get
2a(p – q) + [p(p – 1) – q(q – 1)d] = 0
or 2a(p – q) + [p² – q² – (p – q)d] = 0
or 2a(p – q) + (p – q)[(p + q) – d] = 0
or (p – q)[2a + (p + q – 1)d] = 0
⇒ 2a + (p + q – 1)d = 0
Sum of first (p + q) terms = \(\frac{p+q}{2}\)[2a + (p + q – 1)d]
= \(\frac{p+q}{2}\) × 0 = 0
[∵ 2a + (p + q – 1)d = 0 from (3)]

Question 11.
Sum of the first p, q and r terms of an A.P. are a, b and c respectively. Prove that \(\frac{a}{p}\)(q – r) + \(\frac{b}{q}\)(r – p) + \(\frac{c}{r}\)(p – q) = 0.
Solution:
Let A be the first term and D be the common difference of A.P.
S_p = a.

Multiplying (1) by (q – r), (2) by (r – p), (3) by (p – q) and adding we get
A(q – r + r – p + p – q) + \(\frac{1}{2}\)[(p – 1)(q – r)(r – q) + (r – 1)(p – q)]D
= \(\frac{a}{p}\)(q – r) + \(\frac{b}{q}\)(r – p) + \(\frac{c}{r}\)(p – r)
⇒ A(0) + \(\frac{1}{2}\)(0)D = \(\frac{a}{p}\)(q – r) + \(\frac{b}{q}\)(r – p) + \(\frac{c}{r}\)(p – r).
Hence, \(\frac{a}{p}\)(q – r) + \(\frac{b}{q}\)(r – p) + \(\frac{c}{r}\)(p – q) = 0.

Question 12.
The ratio of the sums of first m and the terms of an A.P. is m² : n². Show that the ratio of mth and nth terms is 2m – 1 : 2n – 1.
Solution:
Let a be the first term and d be the common difference of A.P.

i.e; We are to find the value of \(\frac{a+(m – 1)d}{a+(n – 1)d}\) = \(\frac{2a+(2m-2)d}{2a+(2n-2)d}\)
L.H.S. of (1) will be identical with (2), if (m – 1) replaces (2m – 2) and (n – 1) replaces (2n – 2). So, replacing m by 2m – 1 and n by 2n – 1 on both sides of (1), we get
\(\frac{2a+(2m-2)d}{2a+(2n-2)d}\) = \(\frac{(2m-1)}{(2n-1)}\).

Question 13.
If the sum of first re terms of an A.P. is 3n² + 5n and its mth term is 164, find the value of m?
Solution:
Let the sum of first re terms be denoted by S_p.
∴ S_n = 3n² + 5n.
Put n = 1 and 2.
T₁ = S₁ = 3.1² + 5.1 = 3 + 5 = 8.
S₂ = T₁ + T₂ = 3.2² + 5.2 = 12 + 10 = 22.
∴ T₂ = S₂ – S₁ = 22 – 8 = 14.
∴ Common difference d = T₂ – T₁ = 14 – 8 = 6.
a = 8, d = 6.
mth term = a + (m – 1)d = 164.
or 8 + (m – 1)6 = 164.
⇒ 6m + 2 = 164 or 6m = 164 – 2 = 162.
∴ m = \(\frac{162}{6}\) = 27.

Question 14.
Insert five numbers between 8 and 26 such that the resulting sequence is an A.P.
Solution:
Let the five numbers be denoted by T₂, T₃, T₄, T₅ and T₆.
∴ 8, T₂, T₃, T₄, T₅, T₆ and 26 are in A.P.
26 is the 7th term. If d is the common difference,
then T₇ = a + (7 – 1)d.
⇒ 26 = 8 + 6d ⇒ 6d = 26 – 8 = 18
∴ d = 3.
So, T₂ = a + d = 8 + 3 = 11,
T₃ = a + 2d = 8 + 16 = 14,
T₄ = a + 3d = 8 + 9 = 17,
T₅ = a + 4d = 8 + 12 = 20,
and T₆ = a + 5d = 8 + 15 = 23.
Required five numbers are 11, 14, 17, 20 and 23.

Question 15.
If \(\frac{a^{n}+b^{n}}{a^{n-1}+b^{n-1}}\) is the A.M. between a and b, then find the value of n?
Solution:
A.M. between a and b = \(\frac{a+b}{2}\)
∴ \(\frac{a^{n}+b^{n}}{a^{n-1}+b^{n-1}}\) = \(\frac{a+b}{2}\)
⇒ 2aⁿ + 2bⁿ = aⁿ + ab^n-1 + a^n-1b + bⁿ
⇒ aⁿ – a^n-1b – ab^n-1 + bⁿ = 0
⇒ a^n-1(a – b) – b^n-1(a – b) = 0
⇒ (a – b)(a^n-1 – b^n-1) = 0 [∵a ≠ 0]
⇒ a^n-1 – b^n-1 = 0
⇒ a^n-1 = b^n-1.
⇒ \(\frac{a}{b}\)^n-1 = 1 = (\(\frac{a}{b}\))⁰
⇒ n – 1 = 0 ⇒ n = 1.

Question 16.
Between 1 and 31, m numbers have been inserted in such a way that the resulting sequence is an A.P. and the ratio of 7th and (m – 1)th numbers is 5:9. Find the value of m?
Solution:
Let A₁, A₂, ……………….. A_m be the m arithmetic means each inserted between 1 and 31.
Total number of terms = m + 2.
If d is the common difference, then
1 + (m + 2 – 1 )d = 31.
⇒ (m + 1)d – 30.
⇒ d = \(\frac{30}{m+1}\).
So, A₇ = T₈ = a + 7d
= 1 + 7 × \(\frac{30}{m+1}\)
= \(\frac{m+1+210}{m+1}\) = \(\frac{m+211}{m+1}\)
Also, A_m-1 = T_m = a + (m – 1)d
= 1 + (m – 1) × \(\frac{30}{m+1}\)
= \(\frac{m+1+30m-30}{m+1}\) = \(\frac{31m-29}{m+1}\)
Now, \(\frac{A_{7}}{A_{m-1}}\) = \(\frac{m+211}{31m-29}\) = \(\frac{5}{9}\).
⇒ 9m + 1899 = 155m – 145
⇒ 146m = 2044
⇒ m = \(\frac{2044}{146}\) = 14
Hence, m = 14.

Question 17.
A man starts repaying a loan as first instalment of ₹ 100. If he increases the instalment by ₹ 5 every month, what amount he will pay in the 30th instalment?
Solution:
The instalments form an A.P., whose first term is ₹ 100 and the common difference is ₹ 5.
∴ 30th instalment = T₃₀ = a + (30 – 1)d
= 100 + 29 × 5
= 100 + 143
= 245.
Thus, the 30th instalment is ₹ 245.

Question 18.
The difference between any two consecutive interior angles of a polygon is 5°. If the smallest angle is 120°, find the number of sides of the polygon?
Solution:
The angles of a polygon of n sides form an A.P., whose first term is 120° and common difference is 5°.
The sum of interior angles (in degrees)
= \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{n}{2}\) [2 × 120 + (n – 1) × 5]
= \(\frac{n}{2}\) [240 + 5n – 5] = \(\frac{n}{2}\)(235 + 5n).
Also, the sum of interior angles (in degrees)
= 180 × n – 360.
∴ \(\frac{n}{2}\)(235 + 5n) = 180n – 360
Multiplying by \(\frac{2}{5}\), we get
n(47 + n) = 2(36n – 72)
= 72n – 144
or n² + (47 – 72)n + 144 = 0.
⇒ n² – 25n + 144 = 0
⇒ (n – 16)(n – 9) = 0
Now, n ≠ 16
∴ n = 9.