GSEB Solutions Class 11 Physics Chapter 14 Oscillations

Gujarat Board GSEB Textbook Solutions Class 11 Physics Chapter 14 Oscillations Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Physics Chapter 14 Oscillations

GSEB Class 11 Physics Oscillations Text Book Questions and Answers

Question 1.
Which of the following examples represent periodic motion?

1. A swimmer completing one (return) trip from one bank of a river to the other and back.
2. A freely suspended bar magnet displaced from its N-S direction and released.
3. A hydrogen molecule rotating about its centre of mass.
4. An arrow released from a bow.

Answer:

1. It is not a period motion. Though the motion of a swimmer is to and fro but will not have a definite period.
2. It is a periodic motion because a freely suspended magnet if once displaced from N-S direction and let it go, it oscillates about this position. Hence it is simple Harmonic motion also.
3. It is a periodic motion.
4. It is not a periodic motion.

Question 2.
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic, but not simple harmonic motion?
(a) The rotation of Earth about its axis.
(b) Motion of an oscillating mercury column in a U-tube.
(c) Motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lower most point.
(d) General vibrations of a polyatomic molecule about its equilibrium position.
Answer:
(a) It is periodic but not simple harmonic motion (S.H.M.) as it is not to and fro motion about a fixed point.

(b) It is S.H.M.

(c) It is S.H.M.

(d) It is periodic but not S.H.M. A polyatomic molecule has a number of natural frequencies and its general motion is the resultant of S.H.M.’s of a number of different frequencies. This superposition (i.e. resultant motion) is periodic but not simple harmonic motion.

Question 3.
Given below are four x-t plots for linear motion of a (article. Which of the plots represent periodic motion? What is he period of motion (in case of periodic motion)?

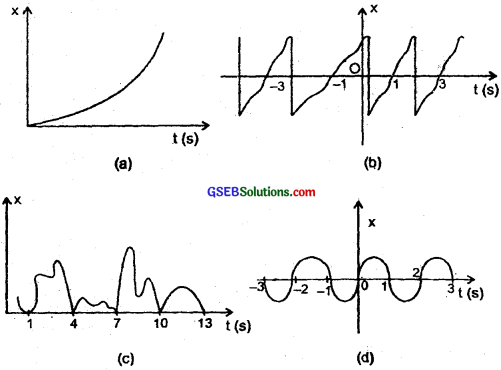
Answer:
(a) It does not represent periodic motion as the motion neither repeats nor comes to mean position.
(b) It represents periodic motion with period equal to 2s.
(c) It does not represent periodic motion because it does not repeat identically.
(d) It represents periodic motion having period equal to 2s.

Question 4.
Which of the following functions of time represent (i) Simple harmonic, (ii) periodic but not simple harmonic and (iii) non-periodic motion? Give period for each case of periodic motion: (to is any positive constant)
(а) Sin ωt – cosωt.
(b) Sin³3ωt.
(c) 3cos(\(\frac{π}{4}\) – 2ωt).
(d) cos ωt + cos 3ωt + cos 5ωt.
(e) exp (-ω²t²).
(f) 1 + ωt + ω²t².
Answer:
A function will represent a periodic motion, if it is identically repeated after a fixed interval of time and will represent S.H.M. if it can be written uniquely in the form of a cos (\(\frac{2π}{T}\)t + ϕ) or sin (\(\frac{2π}{T}\)t + ϕ) where T is the time period.
(a) sin ωt – cos ωt = \(\sqrt{2}\)(\(\frac{1}{\sqrt{2}}\) sin ωt – \(\frac{1}{\sqrt{2}}\) cos ωt)
= \(\sqrt{2}\)(sin ωt cos \(\frac{π}{4}\) – cos ωt sin \(\frac{π}{4}\))
= \(\sqrt{2}\) sin(ωt – \(\frac{π}{4}\))
∴ It represents simple harmonic with a period T = \(\frac{2π}{ω}\) and a phase angle (-\(\frac{π}{4}\)) or \(\frac{7}{4}\) π.

(b) sin²ωt = \(\frac{π}{4}\)(3 sin ωt – sin3ωt)
(∵ sin 3A = 3 sin A – 4 sin³A)
Here each term sin 3ωt and sn 3ωt individually represents S.H.M. but it is not outcome of superposition of two S.H.Ms., so it will represent only periodic but not simple harmonic. Its time period = \(\frac{2π}{ω}\).

(c) 3 cos(\(\frac{π}{4}\) – 2ωt) = 3 cos (2ωt – \(\frac{π}{4}\))
[∵ cos(-θ) = cos θ]
It represents simple harmonic and its time period is \(\frac{2π}{2ω}\) = \(\frac{π}{ω}\).

(d) cos ωt + cos 3ωt + cos 5ωt
It represents periodic but not simple harmonic motion. Its time period is \(\frac{2π}{ω}\). It can be noted that each term represents a periodic function with a different angular frequency. Since period is the least interval of time after which a function repeats its value, cos ωt has a period T = \(\frac{2π}{ω}\), cos 3ωt has a period \(\frac{2π}{3ω}\) = \(\frac{T}{3}\), and cos 5ωt has a period \(\frac{2π}{5ω}\) = \(\frac{T}{5}\), the last two forms repeat after any integral multiple of their period. Thus each term in the sum repeats itself after T, and hence the sum is a periodic function with a period \(\frac{2π}{ω}\).

(e) exp (-ω²t²):
It is an exponential function which decreases monotonically with increasing time and tends to zero as t →∞ and thus never repeats itself. Therefore it represents non – periqdie motion.

(f) 1 + ωt + ω²t². It also represents non-periodic motion (physically unacceptable because the function tends to infinity as t → ∞.

Question 5.
A particle is in linear simple harmonic motion between two points A and B 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A.
(b) at the end B.
(c) at the mid point of AB going towards A.
(d) at 2 cm away from B going towards A.
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
Answer:
Let the situation be depicted as per figure here.
AB = 10 cm (given), P = mid – point of AB

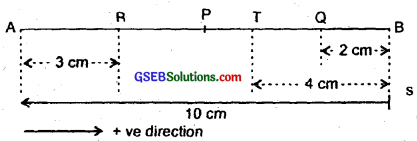
Here, A and B represent the two extreme positions of a S.H.M. For velocity, the direction from A to B is taken as +ve. For acceleration and the force, the direction is taken to be positive if directed along AP and negative if directed along BP.
(a) At the end A, the particle executing S.H.M. is momentarily at rest being its extreme position of motion, hence its velocity is zero, acceleration is +ve as it is directed along AP. Force is also +ve as the force is directed towards AP.
Answer:
0, +, +.

(b) At end B, velocity is zero. Here the acceleration and force are negative as they are directed along BP i.e. along negative direction.
Answer:
0, -, -.

(c) At the mid point of AB going towards A, the particle is at the mean position P, with a tendency to move along PA i.e. negative direction. Hence velocity is -ve, and both acceleration and force are zero.
Answer:
-, 0, 0.

(d) At 2 cm away from B going towards A, the particle is at point Q with a tendency to move along QP which is negative direction. Here, therefore velocity, acceleration and force all are -ve. i.e.
Answer:
-, -, –

(e) At 3 cm away from A going towards B. The particle is now at R with a tendency to move along RP. i.e. in +ve direction. So velocity, acceleration and force are all be +ve i.e.
Answer:
+, +, +.

(f) At 4 cm away from B going towards A. The particle is at T with a tendency to move along TP which is -ve direction for velocity. So velocity is -ve, acceleration and force are directed along TP. Hence both are -ve.
Answer:
-, – , -.

Question 6.
Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(а) a = 0.7x
(b) a = – 200x²
(c) a = – 10x
(d) a = 100x³.
Answer:
A particle is said to be executing S.H.M. if the acceleration (a) produced in it satisfies the following two conditions:
(i) ‘a’ directly proportional to the’ displacement (sayty) from the mean position i.e. a ∝ y.
(ii) ‘a’ is directed towards mean position, i.e. acts opposite to the direction in which y increases.
i.e. mathematically a = -ω²y)
where ω = angular frequency.
(a) a = 0.7x does not satisfy eqn.(1), so it does not represent S.H.M.
(b) a = – 200x², does not satisfy eqn. (1), hence it does not represent S.H.M.
(c) a = – 10x, here x = displacement. It satisfies eqn. (1), so it represents S.H.M.
(d) a = 100x³ again does not represent S.H.M.

Question 7.
The motion of a particle executing S.H.M. is described by the displacement function: x(t) = A cos (ωt + ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is πs^-1. If instead of the cosine function, we choose the sine function to describe the S.H.M.: x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions?
Answer:
(a) x(t) = A cos (ωt + ϕ) …………………. (1)
At t = 0, ω = πs^-1, ∴ x = 1 cm,
v = ω = π cms^-1 …………………….. (2)
∴ From (1) and (2), we get
1 = A cos (π × 0 + ϕ)
= A cos ϕ
Also ω = \(\frac{2π}{T}\), ∴ T = \(\frac{2π}{ω}\) = \(\frac{2π}{π}\) = 2s.
Differentiating (1), with respect to t, we get
\(\frac{d}{dt}\)(x) = – A sin(ωt + ϕ) (ω)
= – A ω sin (ωt + ϕ)
v = – A ω sin (ωt + ϕ) …………………… (4)
Again from (2) and (4), we get
π = – A × π × sin(ω × 0 + ϕ)
= – A sin ϕ
or 1 = – A sin ϕ ………………….. (5)
Squaring (2) and (5) and adding, we get
1² + 1² = A²(sin²ϕ + cos²ϕ) = A²
∴ A = \(\sqrt{2}\) cm.
Dividing (5) by (3), we get
1 = – \(\frac{sinϕ}{cosϕ}\) = – tan ϕ
or tan ϕ = – 1 = – tan \(\frac{π}{4}\)
= tan (2π – \(\frac{π}{4}\))
= tan \(\frac{7π}{4}\)
∴ ϕ = \(\frac{7}{4}\)π.

(b) If x = B sin (ωt + α)
or x = Bcos [(ωt + α) – \(\frac{π}{2}\)] ……………………… (6)
Using the initial conditions as in (a) i.e. at t = 0, x = 1 cm
∴ v = πcms^-1, ω = π s^-1, we get
∴ 1 = B cos (π × 0 + α – \(\frac{π}{2}\))
= B cos (α – \(\frac{π}{2}\)) …………………… (7)
Also let v = velocity in this case,
∴ v’ = \(\frac{d}{dt}\)(x)
= – Bω sin (ωt + α – \(\frac{π}{2}\))
or π = – B × π sin (π × 0 + α – \(\frac{π}{2}\))
= – Bπ sin(α – \(\frac{π}{2}\))
= – Bπ sin(α – \(\frac{π}{2}\))
or 1 = – B sin (α – \(\frac{π}{2}\)) …………………….. (8)
(7)² + (8)² gives,
1² + 1² = B²[sin²(α – \(\frac{π}{2}\)) + cos²(α – \(\frac{π}{2}\))
or 2 = B²
∴ B = \(\sqrt{2}\) cm.
\(\frac{(g)}{(7)}\) gives, 1 = – tan(α – \(\frac{π}{2}\))
or tan (α – \(\frac{π}{2}\)) = – 1 = – tan \(\frac{π}{4}\))
= tan (2π – \(\frac{π}{4}\)) = tan \(\frac{7π}{4}\))
or α – \(\frac{π}{2}\) = \(\frac{7π}{4}\)
or α = \(\frac{7π+2π}{4}\) = \(\frac{9π}{4}\)
= 2π + \(\frac{π}{4}\)
∴ α = \(\frac{π}{4}\).

Question 8.
A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6s. What is the weight of the body?
Answer:
Here, m = 50 kg
Maximum extension, y – 20 – 0 = 20 cm = 0.2 m
T = 0.6s
∴ Maximum force, F = mg = 50 × 9.8 = 490.0 N
∴ Spring Constant, k = \(\frac{F}{y}\) = \(\frac{490}{0.2}\)
= \(\frac{490×10}{2}\) = 2450 Nm^-1
Now we know that the time period is given by
T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
or T² = 4π² \(\frac{m}{k}\)
or m = \(\frac{T^{2} k}{4 \pi^{2}}\) = \(\frac{(0.6)^{2} \times 2450}{4 \times 9.87}\) = 22.36 kg
∴ weight of the body, W = mg = 22.36 × 9.8 = 219.1 N
= 22.36 kgf.

Question 9.
A spring having a spring constant 1200 Nm^-1 is mounted on a horizontal table as shown. A mass of 3.0 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine

1. the frequency of oscillations.
2. the maximum acceleration of the mass, and
3. the maximum speed of the mass?
   

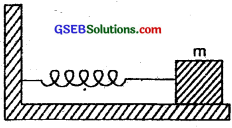
Answer:
Here, k = 1200 Nm^-1
m = 3.0 kg
A = 2.0 cm = 0.02 m
= maximum displacement

1. We know that, T = 2π\(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\)
Also we know that frequency,
v = \(\frac{1}{T}\)
∴ v = \(\frac{1}{2π}\)\(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\) = \(\frac{1}{2×3.142}\) × \(\sqrt{\frac{\mathrm{1200}}{\mathrm{3}}}\)
= \(\frac{20}{2×3.142}\) = 3.18
∴ v = 3.18 s^-1 = 3.2 s^-1.

2. The acceleration is given by
a = – ω²x = – \(\frac{k}{m}\) x
or |a_max| = \(\frac{k}{m}\) |X_max|, where ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\)
i.e. acceleration will be maximum, when x is maximum.
i.e. x = A = 0.02 m
∴ a = \(\frac{1200}{3}\) × 0.02 = 8.0 ms^-1.

3. The maximum speed of the mass is given by
v = Aω = A\(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\) = 0.02 × \(\sqrt{\frac{\mathrm{1200}}{\mathrm{3}}}\)
= 0.02 × 20 = 0.40 ms^-1.

Question 10.
In exercise 14.9 let us take the position of mass when the spring is unstretched as x = 0, and the direction from left to right as the positive direction of x – axis. Give x as a function of time t for the oscillating mass if at the moment we start the stopwater (t = 0), the mass is
(a) at the mean position.
(b) at the maximum stretched position.
(c) at the maximum compressed position.
In what way do these different functions for S.H.M. differ from each other in frequency, in amplitude or the initial phase?
Answer:
Since the position of mass is taken when x = 0, so the equation of displacement in x direction is given by
x = Asinωt.
(∵ initial phase Ø = \(\frac{π}{2}\))
From Question 14.9, A = 2cm = 0.02 m
k = 1200 Nm^-1
ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\) = \(\sqrt{\frac{\mathrm{1200}}{\mathrm{3}}}\) = 20 s^-1

(a) When the mass is at the mean position, then from equation (1), we get
x = 2 sin 20t ……………………… (2)

(b) In the maximum stretched position of the spring, Ø = \(\frac{π}{2}\)
∴ x = Asin(ωt + Ø)
= 2 sin (20t + \(\frac{π}{2}\))
= 2 cos 2ot …………………….. (3)

(c) At the maximum compressed position
Ø = \(\frac{π}{2}\) + \(\frac{π}{2}\) = \(\frac{2π}{2}\)
∴ x = A sin (ωt + ϕ)
= A sin (ωt + \(\frac{2π}{2}\))
= – A cos ωt
∴ x = A cos ωt = – 2 cos (20t) ……………………….. (4)
From equation (2), (3) and (4), we see that the function differ only in initial phase because their amplitude (A = 2 cm) and periods are same i.e. T = \(\frac{2π}{ω}\) = \(\frac{2π}{20}\) = \(\frac{π}{10}\) rad s^-1.

Question 11.
Figure below corresponds to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clock-wise or anticlock-wise) are indicated on each figure. Obtain the corresponding simple harmonic motion of the x-projection of the radius vector of the revolving particle P, in each case.

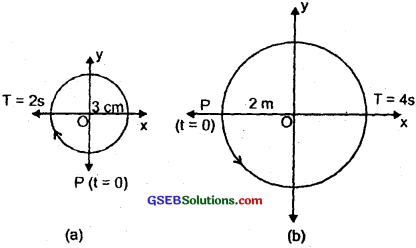
Answer:
(a) Here, at t = 0, OP makes an angle \(\frac{π}{2}\) with x-axis. Since motion is clock-wise so ϕ = radian. Thus the x-projection of OP at time t will give us the equation of S.H.M. given by:

= – 3 sin πt
∴ x = – 3 sin πt. (cm)

(b) Here, T = 4s, A = 2m
At t = 0, OP makes an angle 7t with the positive direction of x-axis i.e. ϕ = +π.
Thus the x-projection of OP at time t will give us the equation of S.H.M given by:

Aliter:
(a) At t = 0, A = – 3 cm, T = 2s, ϕ = 0 motion is clock-wise.
∴ eqn. of S.H.M. is
x = A sin (\(\frac{2π}{T}\)t + ϕ)
= – 3 sin (\(\frac{2π}{2}\)t)
= – 3 sin (πt)

(b) A = 2m, at t = 0, T = 4s, ϕ = π, motion is anticlock-wise,
∴ equation of S.H.M is

Question 12.
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity the snese of rotation may be fixed to be anticlock-wise in every case; (x is in cm and t is in s).
(a) x = – 2 sin (3t + \(\frac{π}{3}\))
(b) x = cos (\(\frac{π}{6}\) – t)
(c) x = 3 sin (2πt + \(\frac{π}{4}\))
(d) x = 2 cos πt.
Answer:
Here,

The corresponding reference circle-is as shown in Fig. (a). Comparing eqn. (4) with eqn. (3). we get A = cos (ωt + ϕ), we get
T = \(\frac{2π}{3}\), ϕ = \(\frac{5π}{6}\), A = 2cm.

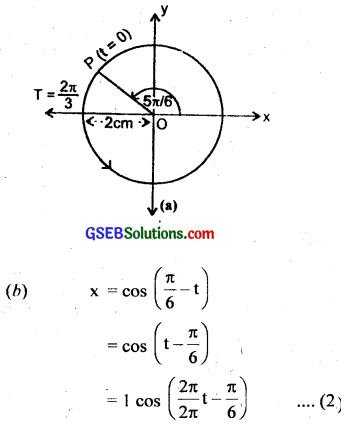
The corresponding reference circle is as shown in Fig. (b). Comparing equation (2) with
x = A cos (\(\frac{2π}{T}\)t + ϕ) ……………………… (3)
We get here, A = 1 cm, T = 2π, ϕ = – \(\frac{π}{6}\).

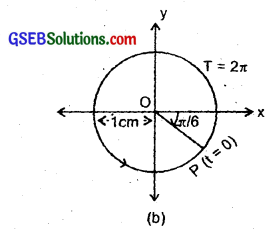
(c) Comparing eqn. (4) with eqn. (3), we get
A = 3 cm
T = 1 s
ϕ = – \(\frac{π}{4}\)

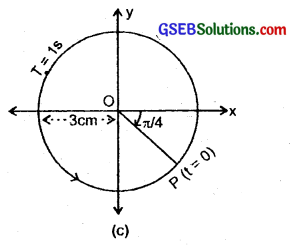
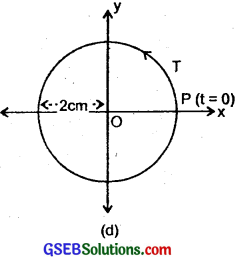
(d) x = 2 cos πt
= 2 cos (\(\frac{π}{1}\)t + 0) …………………… (5)
The corresponding reference circle is as shown in Fig.
(d). Comparing equation (3) with (5), we get
A = 2 cm, T = 1s, ϕ = 0.

Question 13.
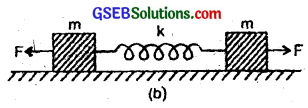
Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass m at either end. Each of the spring in figure (b) is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases.

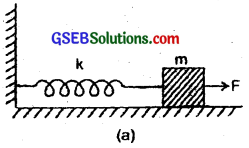
(b) If the mass in figure (a) and the two masses in figure (b) are released free, what is the period of oscillation in each case?

Answer:
Here, k = force constant of the spring.
m = mass attached to free ends.
F = force applied at the free end.

Case (1):
(a) Let a = acceleration produced in the mass ‘m’ attached to the free end due to the force F applied.
∴ F = ma ……………………… (i)
Let y₁ be the extension produced in the spring in Fig. (a).
F = – ky₁ ………………….. (ii)
∴ From (i) and (ii), we get

where y is the displacement equal to y₁.
Also we know that a = – ω²y …………………….. (iv)
∴ From (iii) and (iv), we get
ω² = \(\frac{k}{m}\)
or ω = \(\sqrt{\frac{\mathrm{k}}{\mathrm{m}}}\) …………………… (v)
∴ Maximum extension produced in the string is y₁ = y.
or y₁ = \(\frac{F}{k}\)

(b) From equation (iv), we see that a = y, and the mass is executing S.H.M.
∴ If T ₁ be the time period of oscillation of mass m, then

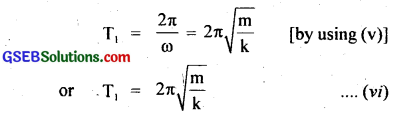
Case (2):
(a) Let y₂ be the total extension produced in the spring when the two masses are released. As masses are equal, so if y be the extension produced in the spring due to each mass, then
y₂ = y’ + y’ = 2y’
Also as explained in case 1 (a),
y₂ = \(\frac{F}{k}\)
∴ \(\frac{F}{k}\) = 2y’
or y’ = \(\frac{1}{2}\)\(\frac{F}{k}\)
i.e. displacement of each mass, y’ = \(\frac{1}{2}\)\(\frac{F}{k}\)
∴ y₂ = 2.\(\frac{F}{2k}\) = \(\frac{F}{k}\)
∴ acceleration produced in each mass is then

(b) If T₂ be the time period of oscillation of mass m, then

Aliter:
Let µ = reduced mass of the system for fig. (b) = inertia factor

Question 14.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 m. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/ min, what is its maximum speed?
Answer:
Stroke of piston = 2 times the amplitude
Let A = amplitude, Stoke = 1 m (given)
∴ 1 = 2A
or A = \(\frac{1}{2}\) m
Angular frequency, ω = 200 rad/min
V_max = maximum speed = ?
We know that the maximum speed of the block when the amplitude is A is given by
V_max = ωA = 200 × \(\frac{1}{2}\) = 100 m/min
= \(\frac{100}{60}\)ms^-1 = \(\frac{5}{3}\)ms^-1 = 1.67 ms^-1

Question 15.
The acceleration due to gravity on the surface of moon is 1.7 ms^-2. What is the time period of a simple pendulum on the surface of moon if its time-period on the surface on Earth is 3.5 s? (g on the surface of Earth is 9.8 ms^-2.)
Answer:
Let T = time period on the surface of Earth
= 3.5 s
T_m = time period on the surface of Moon = ?
g_c = acceleration due to gravity on the surface of earth = 9.8 ms^-2
l = length of the simple pendulum
Using the formula

Dividing (2) by (1), we get

Question 16.
Answer the following questions:
(a) Time period of a particle in S.H.M. depends on the force constant k and mass m of the particle: T = 2π \(\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}\). A simple pendulum executes S.H.M. approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?
(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, of a more involved analysis shows that T is 2π\(\sqrt{\frac{\mathrm{l}}{\mathrm{g}}}\) greater than. Think of a qualitative argument to appreciate this result.
(c) A man with a wrist watch on his hand falls from the top of a tower. Does the watch give the correct time during free fall?
(d) What is the frequency of oscillation of simple pendulum in a cabin that is freely falling under gravity?
Answer:
(a) For a simple pendulum,
F = – \(\frac{mg}{l}\)y = – ky
∴ k = \(\frac{mg}{l}\)
where k = spring factor or force constant which is proportional to the mass m of the particle. Also time period of simple pendulum is given by

Thus m cancels out in denominator as well as in numerator. That is why the time period of simple pendulum is independent of the mass of the bob.

(b) The effective restoring force that brings the bob back to its mean position in case of simple pendulum is F = – mg sin θ.
when θ is small, sin θ ~ θ and the expression for time period of the simple pendulum is given by
T = 2π\(\sqrt{\frac{\mathrm{l}}{\mathrm{g}}}\)
Now for larger values of θ, we will take F = – mg sin θ which is definitely < mgθ as sin θ < θ for larger values of θ. Thus the effective value of g becomes g sin θ for larger θ. Thus clearly g sin θ < g. As T ∝ \(\frac{1}{\sqrt{\mathrm{g}}}\), so for larger values of θ, effective value of g decreases and hence T increases beyond T = 2π\(\sqrt{\frac{\mathrm{l}}{\mathrm{g}}}\)

(c) Yes, it gives correct time during free fall. The working of the wrist watch depends on the spring action i.e. spring wound watch runs due to P.E. stored in the spring. Acceleration due to gravity plays ho role in the working of a watch. So it gives correct time.

(d) We know that the frequency of oscillation of simple pendulum is given by
v = \(\frac{1}{T}\) = 2π\(\sqrt{\frac{\mathrm{g}}{\mathrm{l}}}\)
i.e. v ∝ \(\sqrt{g}\)
As g = 0 i.e. gravity disappears for a freely falling body, so frequency is zero.

Question 17.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium position, what will be its time period?
Answer:
Since the pendulum is oscillating in the radial direction, it is acted upon by an additional acceleration equal to the centripetal acceleration of the car on the circular track of radius R i.e. \(\frac{v^{2}}{R}\) where v = uniform speed of the car. Thus, there are two accelerations acting on the pendulum in mutually perpendicular directions.
i.e. (i) acceleration due to gravity (g)
(ii) a_c = centripetal acceleration (\(\frac{v^{2}}{R}\))
If a be the resultant acceleration of the pendulum, then

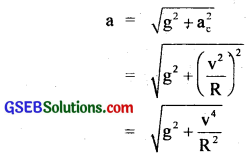
If T be the time period of oscillation of the pendulum, then

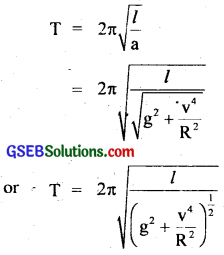
i.e. the effective acceleration due to gravity gets reduced due to radial acceleration \(\frac{v^{2}}{R}\) acting in the horizontal plane.

Question 18.
A cylindrical piece of cork of base area A and height h floats in a liquid of density ρ_l. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T = 2π\(\sqrt{\frac{\mathrm{h\rho}}{\rho_{1} g}}\), where ρ is the density of the cork. (Ignore damping due to viscosity of the liquid.)
Answer:
Let X be the equilibrium position of a cylinder floating in a given liquid.
Let A = area of cross-section of the cylindrical piece of cork,
h = height of the cylindrical piece of cork,
ρ = density of the material of the cylindrical cork.

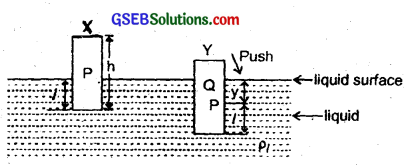
ρ_e = density of the liquid in which it floats.
l = length of the cylindrical piece of cork dipping in the liquid upto point P in position X.
W = weight of the cylinderical cork.
W₁ = weight of the liquid – displaced by the cork.
V = its volume.
m = mass of cork = Ahρ.
∴ V = Ah
W = mg = (Vρ)g = (Ahρ)g
∴ W₁ = Area of cross-section of cork × length of cylinder dipping in liquid × density of liquid × g = A l ρ₁ g. According to the law of floatation,
W = W₁
or Ahρg = A l ρ₁g
or h = \(\frac{l \rho_{l}}{\rho}\) …………………… (1)
Let the cylinder be pushed into the liquid through a distance PQ = y. Then the restoring force acting on the cylinder is given by
F = – weight of the liquid displaced by portion PQ of the cylindrical cork
= – (Ay)ρ₁ × g = (A ρ₁g)y …………………….. (2)
or F = – ky
where k = A ρ₁g is the force constant.
If a be the acceleration produced in the cylindrical piece of cork, then

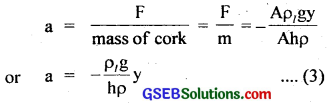
Now as the acceleration of the cylindrical cork is directly proportional to-its displacement from equilibrium position and acts towards the equilibrium position, so the motion of the bob is simple harmonic having time period (T) given by

Question 19.
One end of a U-tube containing mercury is connected to a suction punp and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the liquid column of mercury in the U-tube executes simple harmonic motion?
Answer:
The suction pump creates the pressure difference, thus mercury rises in one limb of the U-tube. When it is removed, a net force acts on the liquid column due to the difference in levels of mercury in the two limbs and hence the liquid column executes S.H.M. which can be explained as:

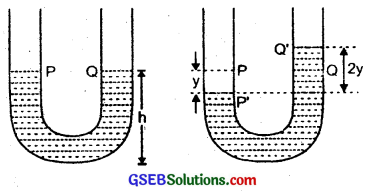
Consider the mercury contained ¡n a vertical U-tube upto the level P and Q in its two limbs.
Let ρ = density of the mercury.
L = total length of the mcruury column in both the limbs.
A = internal cross-sectional area of U-tube.
m = mass of mercuiy in U-tube = LAρ.
Let the mercury be depressed in left limb to P by a small distance y, then it rises by the same amount in the right limb to position Q
∴ Difference in levels in the two limbs PQ’ = 2y
∴ Volume of mercury contained in the column of length 2y
= A × 2y
∴ m = A × 2y × ρ
If W = weight of liquid contained in the column of length 2y
Then W = mg = A × 2y × ρ × g
This weight produces the restoring force (F) which tends to bring back the mercury to its equilibrium position.
∴ F = -2Aýρg = – (2Aρg)y
If a = acceleration produced in the liquid column, then

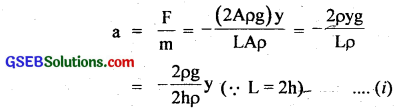
where h height of mercury in each limb. Now from (i). it is clear that a ∝ y and – ve sign shows that ¡tacts opposite toy, so the motion of mercury in U-tube is simple harmonic in nature having time period (T) given by