GSEB Solutions Class 11 Physics Chapter 2 Units and Measurements

Gujarat Board GSEB Textbook Solutions Class 11 Physics Chapter 2 Units and Measurements Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 11 Physics Chapter 2 Units and Measurements

GSEB Class 11 Physics Units and Measurements Text Book Questions and Answers

Question 1.
Fill in the blanks:
(a) The volume of a cube of side 1 cm is equal to ……………………. m³.
(b) The surface area of a solid cylinder of radius 2.0 cm and height 10.0 cm is equal to …………………… (mm)².
(c) A vehicle moving with a speed of 18 kmh^-1 covers ……………………. m in 1s.
(d) The relative density of lead is 11.3. Its density is ………………………… g cm^-3 or …………………… kg m^-3.
Answer:
(a) The volume of a cube of side 1 cm is given by, V = (1 cm)³ or V = (10^-2m)³ = 10^-6m³.

(b) The surface area of a solid cylinder of radius r and height h is given by :
A = Area of two caps + curved surface area
= 2πr² + 2πrh
= 2πr (r + h)
here r = 2 cm = 20 mm, h = 10 cm = 100 mm
∴ A = 2 × \(\frac{22}{7}\) × 20 (20 + 100) (mm)²
= 15099 mm²
= 1.5099 × 10⁴ mm²
= 1.5 × 10⁴ mm²

(c) Here v = 18 kmh^-1 = \(\frac{18×1000m}{3600s}\) = 5 ms^-1
t = 1s
∴ x = υt = 5 × 1 = 5m

(d) Relative density of lead = 11.3,
density of water = 1 gm cm^-3
We know that relative density of lead
=
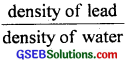
∴ density of lead = realative density of lead × density of water
= 11.3 × 1 gm cm^-3
= 11.3 gm cm^-3

Also in S.I. system density of water = 10³ kg m^-3
∴ density of lead = 11.3 × 10³kgm^-3
= 1.13 × 10⁴kgm^-3
Answer:
(a) 10^-6
(b) 1.5 × 10⁴
(c) 5m
(d) 11.3, 1.13 × 10⁴

Question 2.
Fill in the blanks by suitable conversion of units.
(a) 1 kg m²s^-2 = …………………… g cm² s^-2
(b) 1 m = ly (light year)
(c) 3.0 ms^-2 = ………………….. kmh^-2
(d) G = 6.67 × 10^-11 Nm² kg^-2 = ……………………… cm³ s^-2 g^-1.
Answer:
(a) 1 kg m²s^-2 = 1 (10³g) (10²cm²)s^-2
= 10³ × 10⁴g cm²s^-2
= 10⁷g cm²s^-2

(b) 1 light year (ly) = 9.46 × 10¹⁵m
∴ 1m = \(\frac{1}{9.46 \times 10^{15}}\)ly = 1.057 × 10^-16ly

(c) 3.0 ms^-2 = 3 × 10^-3 km × (\(\frac{1}{60×60}\) h^-1)^-2
= 3 × 10^-3 × (3600)² kmh^-2
= 3.888 × 10⁴ kmh^-2
= 3.9 × 10^-4 kmh^-2

(d) G = 6.67 × 10¹¹ Nm²kg^-2
= 6.67 × 10^-11 (10⁵ dyne) (10² cm)² (10³ g)^-2
= 6.67 × 10^-11 × 10⁵ × 10⁴ × 10^-6 dyne cm² g^-2
= 6.67 × 10^-8 (g cm s^-2) cm² g^-2
= 6.67 × 10^-8 cm³ g^-1 s^-2.

Question 3.
A calorie is a unit of heat or energy and it equals about 4.2 J, where 1J = 1 kg m²s^-2. Suppose we employ a system of units in which the unit of mass equals akg, the unit of length βm, the unit of time is γs. Show that a calorie has a magnitude. 4.2α^-1β^-2γ² in terms of new units?
Answer:
We know that n₁u₁ = n₂u₂

1 cal = 4.2 J = 4.2 kg m²s^-2,
∴ a = 1, b = 2, c = -2

SI system:
n₁ = 4.2
M₁ = 1 kg
L₁ = 1 m
T₁ = 1 s

New system:
n₂ = ?
L₂ = α kg
L₂ = β m
T₂ = γ s

∴ n₂ = 4.2\(\frac{1kg}{αkg}\)¹ \(\frac{1m}{βm}\)² \(\frac{1s}{γs}\)]^-2
n₂ = 4.2 α^-1 β^-2 γ²
∴ 1 cal = 4.2 α^-1 β^-2 γ² in new system
Hence proved.

Question 4.
Explain the statement clearly:
“To call a dimensional quantity ‘large’ or ‘small’ is meaningless without specifying a standard for comparison.” In view of this, reframe the following statements wherever necessary:

1. Atoms are very small objects.
2. A jet plane moves with great speed.
3. The mass of Jupiter is very large.
4. The air inside this room contains a large number of molecules.
5. A proton is much more massive than an electron.
6. The speed of souqd is much smaller than the speed of light.

Answer:
The statement is true. The physical quantities are called large or small in comparison to some standard (or the unit) of measurement, eg., the distance between two cities on Earth is measured in kilometres but the distance between stars or intergalactic distances are measured in Parsec. The latter standard Parsec is 3.08 × 10¹⁶m or 3.08 × 10¹³ km is larger than metre or km. Therefore intersteller or inter-galactic distances are certainly larger than the distances between two cities on Earth.

1. The size of an atom is smaller than the sharp tip of a pin.
2. A jet plane moves faster than a superfast train.
3. The mass of Jupiter is very large as compared to the mass of Earth.
4. The air inside this room contains more number of molecules than in one mole of air.
5. The statement is already correct.
6. The statement is already correct.

Question 5.
A new unit of length is chosen such that the speed of light in vaccum is unity. What is the distance between the Sun and the Earth in terms of the new unit of light takes 8 min and 20s to cover this distance?
Answer:
We are given that velocity of light in vacuum, c = 1 new unit of length s^-1.
Time taken by light of sun to reach the Earth, t = 8 min 20s
= 8 × 60 + 20 = 500s
∴ distance between the Sun and the Earth,
x = c × t = 1 new unit of length s¹ × 500s
= 500 new units of length
Aliter: Distance between Sun and Earth
= speed of light in vacuum × time taken by light to travel from Sun to Earth.
= 3 × 10⁸ms^-1 × 500s = 500 × 3 × 10⁸m
In the new system, the speed of light in vacuum is unity
∴ the new unit of length is 3 × 10⁸ m
∴ distance between Sun and Earth = 500 new units.

Question 6.
Which of the following is the most precise device for measuring length:

1. A vernier callipers with 20 divisions on the sliding scale.
2. A screw gauge of pitch 1 mm and 100 divisions on the circular scale.
3. An optical instrument that can measure length to within a wavelength of light?

Answer:
The most precise device is that whose least count is minimum. Now:
1. Least count of vernier callipers
= 1 MSD – 1 VSD .
= 1 MSD – \(\frac{19}{20}\) MSD = \(\frac{1}{20}\) MSD
= \(\frac{1}{20}\)mm = \(\frac{1}{200}\) cm
= 0.005 cm

2.
= \(\frac{1}{100}\) mm = \(\frac{1}{1000}\) cm
= 0.001 cm

3. Wavelength of light, λ ≈ 10^-5 cm = 0.00001 cm
∴ Least count of optical instrument = 0.00001 cm
Thus, clearly the optical instrument is the most precise.

Question 7.
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5mm. What is the estimate on the thickness of hair?
Answer:
Estimate on the thickness of hair is given by:

= \(\frac{3.5mm}{100}\) = 0.035 mm
= 3.5 × 10² mm.

Question 8.
Answer the following:
(a) You are given a thread and a metre scale. How will you estimate the diametre of the thread?
(b) A screw gauge has a pitch of 1.0mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
(c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurement of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
Answer:
(a) The diameter of a thread is so small that it cannot be measured using a metre scale. We wind the thread on in close turns on a pencil or a cylindrical glass rod so that the turns touch one another and are tight. Count the number of turns(n) and find the average length(l) of the coiled thread using the metre scale. Divide this average length by the number of turns to get the diameter i.e.

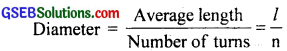
(b) Yes, the accuracy of the gauge increases by increasing the number of divisions of the circular scale because the least count is given by:

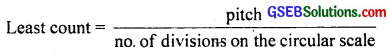
Practically, it may not be possible to take the reading precisely due to low resolution of human eye.
(c) By taking a large number of observations (100) and then taking their mean for the result, greatly reduces, the random error as compared by taking only five observations and then taking their mean. Therefore a set of 100 measurements of the diameter is expected to yield a more reliable estimate than a set of 5 measurements yield only.

Question 9.
The photograph of a house occupies an area of 1.75 cm² on a 35mm slide. The slide is projected on to a screen and the area of the house on the screen is 1.55m². What is the linear magnification of the projector-screen arrangement?
Answer:
Here, size of an object = Area of object
= 1.75 cm² = 1.75 × 10^-4 m²
Size of the image = Area of the image
= 1.55 m²

∴ Linear magnification = \(\sqrt{8857}\) = 94.1.

Question 10.
State the number of significant figures in the following:

1. 0.007m²
2. 2.64 × 10²⁴ kg
3. 0.2370 g cm^-3
4. 6.320 J
5. 6.032 Nm^-2
6. 0.000 6032 m²

Answer:
The number of significant figures is as given below:

1. 1
2. 3
3. 4
4. 4
5. 4
6. 4

Question 11.
The length, breadth and thickness of a rectangular sheet of metal are 4.234m, 1.005m and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures?
Answer:
Here length, l = 4.234m
breadth, b = 1.005m
thickness, h = 0.0201m = 2.01 cm
Area of the sheet = 2 (lb + bh + hl).
= 2(4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234)
= 8.7209468m²
As the least number of significant figures in thickness is 3,
∴ Area = 8.72 m²
Volume = l × b × h
= 4.234 × 1.005 × 0.0201m³
= 0.0855m³.

Question 12.
The mass of a box measured by a grocer’s balance is 2.3 kg. Two gold pieces of masses 20.15g and 20.17g are added to the box. What is (a) the total mass of the box (b) the difference in the mass of the pieces to correct significant figures?
Answer:
Here, mass of the box, m = 2.300 kg
Mass of one gold piece, m₁ = 20.15g = 0.02015 kg
Mass of second gold piece, m₂ = 20.17g = 0.02017 kg

(a) Total mass = m + m₁ + m₂
= (2.300 + 0.02015 + 0.02017) kg
= 2.34032 kg

As the least number of significant figures in the mass of box is 2, so maximum number of significant figures in the result can be 2
∴ Total mass = 2.3 kg

(b) Difference in masses = m₂ – m₁
= 20.17 – 20.15
= 0.02g
Since there are two significant figures so the difference in masses to the correct significant figures is 0.02g.

Question 13.
A physical quantity P is related to four observables a, b, c, and d as follows: P = a³b²/(\(\sqrt{cd}\))
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2% respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?
Answer:
P = \(\frac{a^{3} b^{2}}{\sqrt{c} d}\)
∴ Relative error in P is given by:
\(\frac{∆P}{P}\) = 3\(\frac{∆a}{a}\) + 2\(\frac{∆b}{b}\) + \(\frac{1}{2}\) \(\frac{∆c}{c}\) + \(\frac{∆d}{d}\)
∴ Percentage error in P is given by:

∴ From(i) and (ii), we get
\(\frac{∆P}{P}\) × 100 = 3 × 1% + 2 × 3% + \(\frac{1}{2}\) × 4% + 2%
= 3 + 6 + 2 + 2 = 13%
The calculation of error clearly shows that the number of significant figures is 2, so the result of P may be rounded off to two significant digits i.e. P = 3.763 = 3.8.

Question 14.
A book with many printing errors contains four different formulae for the displacement y of a particle under going a certain periodic motion:
(a) y = a sin \(\frac{2πt}{T}\)
(b) y = a sin vt
(c) y = (\(\frac{9}{T}\)) sin (t/a)
(d) y = (\(\frac{9}{\sqrt{2}}\)) (sin \(\frac{2πt}{T}\) + cos\(\frac{2πt}{T}\))
(a = maximum displacement of the particle, v = speed of the particle, T = time period of motion). Rule out the wrong formulae on dimensional grounds.
Answer:
Let us use the principle of homogenity of dimensions. If in a given relation, the dimensions of each term are same, then it will be correct, otherwise wrong. The argument of a trigonometrical function i.e. angle is dimensionless. Now here in each case dimensions of L.H.S. is [L] and dimensions of R.H.S. in
(a) = [L] (angle \(\frac{2πt}{T}\) is dimensionless)
(b) = [L]sin[(LT^-1)(T)] = [L]sin[L](angle is not dimensionless here)
(c) = \(\frac{[L]}{[T]}\) sin \(\frac{[T]}{[L]}\) = [LT^-1] (angle is not dimensionless here)
(d) = [L] [sin \(\frac{T}{T}\) + cos \(\frac{T}{T}\)] = [L]
∴ formulae (b) and (c) are wrong.

Question 15.
A famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m₀ of a particle in terms of its speed v and spfeed of light c. (This relation first arose as a consequence of special relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes m = \(\frac{m_{0}}{\left(1-v^{2}\right)^{1 / 2}}\). Guess where to put the missing c?
Answer:
According to the principle of homogeneity of dimensions, powers of M, L, T on either side of the formulae must be equal. For this, on R.H.S., the denominator (1 – v²)^1/2 must be dimensionless. 1 is dimensionless. So factor at v² must be dimensionless i.e. there must be v²/c². Hence the correct formula should be,
m = \(\frac{m_{0}}{\left(1-v^{2}\right)^{1 / 2}}\).

Question 16.
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by Å.1 Å = 10^-10m. The size of the hydrogen atom is about 0.5Å. What is the total atomic volume in m³ of a mole of hydrogen atoms?
Answer:
Here r = 0.5Å
= 0.5 × 10^-10 m
V₁ = Volume of each hydrogen atom
= \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\) × 3.14 × (0.5 × 10^-10)³
= 5.236 × 10^-31m³
According to Avogadro’s hypothesis, one mole of hydrogen contains:
N = 6.023 × 10²³ atoms Atomic volume of 1 mole of hydrogen atoms,
V = NV₁
or V = 6.023 × 10²³ × 5.236 × 10^-31
= 3.154 × 10^-7m³
≅ 3 × 10^-7m³.

Question 17.
One mole of an ideal gas at standard temperature and pressure occupies 22.4L (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen? (Take the size of hydrogen molecule to be about 1Å). Why is this ratio so large?
Answer:
d = diameter of hydrogen molecule = 1Å
Molar volume of one mole of hydrogen
= 22.4L = 22.4 × 10^-3m³
r = radius of one molecule of hydrogen
= \(\frac{d}{2}\) = 0.5Å
= 0.5 × 10^-10m
Volume of one molecule of hydrogen
= \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\)π(0.5 × 10^-10)³
= 5.236 × 10^-31m³
1 mole has 6.023 × 10²³ atoms or molecules of H₂
∴ Atomic volume of one mole of hydrogen
= 6.023 × 10²³ × 5.236 × 10^-31m³
= 3.154 × 10^-7m³
∴ \(\frac{\text { Molar volume }}{\text { Atomic volume }}=\frac{22.4 \times 10^{-3} \mathrm{~m}^{3}}{3.154 \times 10^{-7} \mathrm{~m}^{3}}\)
= 7.1 × 10⁴
= 7 × 10⁴
The large value of the ratio shows that the inter molecular separation iri a gas is much larger than the size of a mulecule.

Question 18.
Explain this common observation clearly: If you look out of the window of a fast moving train the nearby trees, houses, etc. seem to move rapidly in a direction opposite to the train’s motion, but the distant, objects (hill tops, the moon, the stars etc.) seem to be stationary (In fact, since you are aware that you are moving, these distant objects seem to move with you)
Answer:
The line joining the object to the eye is called the line of sight. When a train moves rapidly, the line of sight of a nearby tree changes its direction of motion rapidly i.e. near objects make greater angle than distant objects. Therefore the trees appear to run in opposite direction.

On the other hand, the angular change i.e. the line of sight of far-off objects (hill tops, the moon, the stars etc) changes its direction extremely slowly and hence the relative shift in their position is negligible. Hence they appear to be stationary i.e. move in the direction of the train i.e. appear to move with the observer in the train.

Question 19.
The principle of ‘parallax’ is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit = 3 × 10¹¹m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1” (second) of arc or so A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1” (second) of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of metres?
Answer:
We know that parallax of θ of a star is the angle made by semi-major axis of the Earth’s orbit ⊥ to the direction of the star as shown in figure.
From parallax method, we know that S = \(\frac{b}{θ}\)

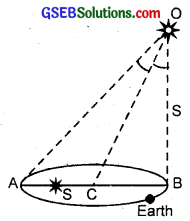
Here θ’ = ∠AOB = 2∠COB = 2θ,
O = position star
b = AB = base line
= Diameter of Earth’s orbit = 3 × 10¹¹m
θ = 1se = 4.85 × 10^-6rad
s = \(\frac{b}{2θ}\) = \(\frac{3 \times 10^{11}}{2 \times 4.85 \times 10^{-6}}\) = 3.09 × 10¹⁶m
Also 1 parasec = 3.08 × 10¹⁶m

Question 20.
The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun?
Answer:
Distance 4.29 light year
= 4.29 × 9.46 × 10¹⁵m (∵ 1 ly = 9.46 × 10¹⁵)
= \(\frac{4.29 \times 9.46 \times 10^{15}}{3.08 \times 10^{16}}\) (∵ 1 parsec = 3.08 × 10¹⁶m)
= 1.318 parsec = 1.32 parsec
Aliter: We know that 326 = ly 1 parsec
∴ 4.29 light year = \(\frac{4.29}{3.26}\) = 1.32 parsec
Required parallax = 2θ. where θ is the annual parallax Since parsec is the distance corresponding to an annual parallax of one second of an arc so, θ = 1.32 second of an arc.
Required Parallax = 2θ where θ is the annual parallex
Since parsec is the distance corresponding to an annual
parallax of one second of an arc so, θ = 1.32 second of an arc.
∴ Required Parallax = 2 × 1.32 = 2.64 second of arc.

Question 21.
Precise measurements ef physical quantities are a need of science. For example, to asertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in Word War II. Think of different examples in modern science where precision measurements of length, time, mass etc. are needed. Also, wherever you can, give a quantitative idea of the precision needed?
Answer:
1. Precision measurement of time and mass are needed for nuclear and atomic reactions, in nuclear weapons, in nuclear power plants etc. (order 10^-9s and 10^-9 kg).

2. Precise location, size and mass of tumor in body are very essential for radio and laser therapy. It is of the order of 10^-9m.

3. The vast applications of laser depend on the interval of time and distance. The time involved is of the order of 10^-9s.

4. The whole range of thin film technology, semiconductor devices depends on the development of precise thickness of the layer of material. The function layer also plays an important role. The common range of these thickness are micro (micrometre µ). Apart from this molecular thick layers in photographic films, metallurgy, anti corrosive electroplating and many other devices are needed.

5. High technological satellite launching and putting in, orbits, super computers, ultra and electron microscopy, spectroscopy all need very precise measurements of mass, length and time from micro (10^-6) to nano (10^-9) or even upto fermi (10^-15m) levels.

Question 22.
Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):
(a) the total mass of rain-bearing clouds over India during the monsoon.
(b) the mass of an elephant.
(c) the wind speed during a storm.
(d) the number of strands of hair on our head.
(e) the number of air molecules in your classroom.
Answer:
Following are the ways of estimation:
(a) Mass of rain water over India = Mass of clouds
= Average rainfall × area of India × density of water
= 10cm × 3.3 × 10¹²m² × 10³ kgm^-3
= 10 × 10^-2m × 3.3 × 10¹⁵ kgm^-1
= 3.3 × 10¹⁴ kg.

(b) The mass of elephant can be estimated with the help principle of lever. It is about 3000 kg for adult one.

Aliter:
We move the elephant into boat of known base area. By measuring depth of boat with elephant in it in the water, we find the volume of water displaced by the boat and the elephant. Subtract from this volume, the volume of water displaced by the empty boat. This gives us the volume of water displaced by the elephant. Multiply this volume by density of, water to obtain the mass of the elephant.

(c) The wind speed can be measured by couple of devices including balloon. The storm speed ranges from 80 kmh^-1 onward. Very intense stroms have a wind speed even upto 300 kmh^-1.

(d)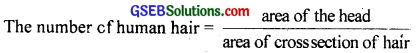
t = the thickness of hair = 5 × 10⁵m = 5 × 10³m
Average radius of human head, r = 8cm
Area of human head A = πr² = π(8)² = 64π cm²
Area of cross section of human hair,
A’ = π\(\frac{\mathrm{t}^{2}}{4}\) = π × \(\frac{25}{4}\) × 10^-6cm²
∴ No.of human hair = \(\frac{64 \pi \times 4}{25 \pi \times 10^{-6}}\) = 10 × 10⁶ = 10⁷.

(e) The number of air molecules in your classroom. We know that one mole of air at NTP occupies a volume of 22.4 litre i.e. 22.4 × 10^-3m³. Measure the volume of the given classroom. Let it be Vm³. Also we know that 1 mole of air contains N no. of atoms,
where N = 6.023 × 10²³ is called
Avogadro’s number
∴ Number of gas or air molecules in the given classroom

Normal classroom size is 5m × 4m × 3m
∴ v = 60m³
Then no. of air molecules = 0.2689 × 10²⁶ × 60
= 16 × 10²⁶ molecules
= 10²⁷ molecules.

Question 23.
The sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding 10⁷K and its outer surface at a temperature of about 6000K. At these high temperatures, no substance remains in a solid or liquid phase. In what range do you expect the mass density of the sun to be, in the range of densities of solids and liquids or gases? Check if your guess is correct from the following data:
Mass of Sun = 2.0 × 10³⁰ kg, radius of the Sun = 7.0 × 10⁸m.
Answer:
Here, M = 2 × 10³⁰kg
R = 7.0 × 10⁸m

This density is in the range of density of solids arid not gases.

Explanation:
The temperature of the inner core of the sun exceeds 10⁷K while the temperature of the outer surface of the sun is nearly 6000K. At such extremely high temperatures, no substancte can exist either in a solid or in a liquid phase. So, the sun is made of ionized matter, i.e., hot plasma. The high density of the plasina is due to the inward gravitational attraction on outer layers due to the inner layers of the sun.

Question 24.
When the planet Jupiter is at a distance of 824.7 million kilometres from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of Jupiter.
Answer:
Here, d = distance of Jupiter from earth
= 824.7 millions kms
or d = 824.7 × 10⁶km
θ = 35.72″ = 35.72 × 4.85 × 10^-6 rad (∵ 1″ = 4.85 × 10^-6 rad)
D = Diameter of Jupiter = ?
∴ using, the relation, θ = \(\frac{D}{d}\), we get
D = θ × d
= 35.72 × 4.85 × 10^-6 × 824.7 × 10⁶km
= 142873 km = 142.873 × 10³km
= 1.42873 × 10⁵km
= 1.429 × 10⁵km.