Gujarat Board GSEB Textbook Solutions Class 11 Physics Chapter 7 System of Particles and Rotational Motion Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 11 Physics Chapter 7 System of Particles and Rotational Motion
GSEB Class 11 Physics System of Particles and Rotational Motion Text Book Questions and Answers
Question 1.
Give the location of the centre of mass of a (i) sphere (ii) cylinder (iii) ring and (iv) cube each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Answer:
C.M. lies at the
- Centre of sphere.
- Mid point of axis of symmetry ofthe cylinder i.e. its geometrical centre.
- Centre of ring.
- Point of intersection of diagonals i.e. at its geometrical centre. No, in some cases, C.M. of a body like ring, hollow cylinder, hollow sphere and hollow cube etc. may lie outside.
![]()
Question 2.
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1Å = 10-10 m). Find the approximate location of the CM of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus?
Answer:
Let CM be at a distance × Å from H atom.
Let m unit = mass of H atom = m1
∴ m2 = mass of Cl atom = 35.5 m unit
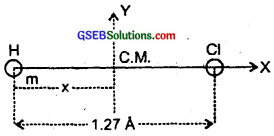
If r1 and r2 be the position vectors of the H and Cl atoms w.r.t. the C.M. as origin i.e. position vector of C.M. is zero
i.e. RC.M. = 0 = \(\frac{\mathrm{m}_{1} \mathbf{r}_{1}+\mathrm{m}_{2} \mathbf{r}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\)
or m1r1 + m2r2 = 0 ……………………. (i)
Here, r1 = -x\(\hat {i} \) and r2 = (1.27 – x)\(\hat {i} \)
∴ From (i),
m(-x\(\hat {i} \)) + 35.5 m(1.27 – x)\(\hat {i} \) = 0
or mx = 35.5m (1.27 – x)
or x + 35.5x = 35.5 × 1.27
∴ x = \(\frac{35.5×1.27}{36.5}\)
= 1235 Å = 1.24 Å from H-atom and on the line joining H and Cl atoms.
Question 3.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the C.M. of the (trolley + child) system?
Answer:
The speed of the centre of mass of the system (i.e. trolley) and child remains unchanged i.e. V, if the child gets up and runs about on the trolley in any manner. It is because the state of system can change only under the effort of an external force and in this case no external force is acting. The forces involved in running on the trolley are from within the system i.e. internal forces.
![]()
Question 4.
Show that the area of the triangle contained between the vectors a and b is one half of the magnitude of a × b.
Answer:
Let the vectors \(\vec{a}\) and \(\vec{b}\) represent the two adjacent sides of ∆AOB such that.
OA = b, OB = a or OA b, OB = a
Let angle between a and b be θ
s.t. ∠AOB = θ
and also let h be the height of the triangle such that
h = AC
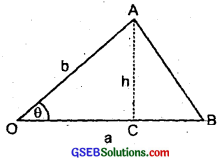
Now in rt. ∠d ∆OCA,
sin θ = \(\frac{AC}{OA}\)
or AC = OA sin θ
or h = b sin θ ………………….. (i)
We know that the area of the triangle AOB, is given by
\(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × OB × AC
= \(\frac{1}{2}\) × a × h
= \(\frac{1}{2}\) × a × b sin θ
= \(\frac{1}{2}\) ab sinθ …………………….. (ii)
Also by the definition of cross-product of two vectors, we know that
a × b = ab sin θ\(\hat {n} \)
or |a × b| = |ab sin θ\(\hat {n} \)|
= ab sin θ|\(\hat {n} \)|
= ab sin θ …………………. (iii) (∵ |\(\hat {n} \)| = 1)
∴ From (ii) and (iii), we get
area of ∆AOB = \(\frac{1}{2}\) |a × b|
= \(\frac{1}{2}\) [magnitude of a × b]
Hence proved.
Question 5.
Show that a.(\(\vec{b}\) × \(\vec{c}\)) is equal in magnitude to the volume of the parallelopiped formed on the three vectors a, b and c.
Answer:
Consider a parallelopiped OABCDEFG with its sides OA, OC and OE such that
\(\overrightarrow{OA}\) = b, \(\overrightarrow{OC}\) = c and \(\overrightarrow{OE}\) = a
∴ b and c represent the two adjacent sides of the parallelogram OABC.
If S be the area of the face OABC which being a parallelogram, then
S = b × c = S\(\hat {n} \)
where \(\hat {n} \) is a unit vector acting along S or perpendicular to the plane containing b and c, S = magnitude of the area of face OABC.
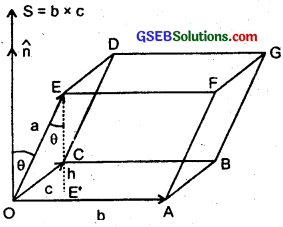
Let θ = angle made by a with S, then
a. (b × c) = a.S = a . \(\hat {n} \)S
= a cos θ S (∵|\(\hat {n} \)| = 1)
= (a cos θ)S
= hS …………………. (i)
where h = a cos θ = length of the perpendicular EE’ from the terminus of a on the surface of the parallelogram OABC = height of the vector a.
Also let V = volume of the parailelopiped OABCDEFG,
∴ V = area of the face OABC × normal from E on the face OABC = S × h …………………… (ii)
∴ from (i) arid (ii), we get
V = a. (b × c) Hence proved.
![]()
Question 6.
(a) Find the components along X, Y amd Z axis of the angular momentum L of a particle, whose positiqn vector is r with components x, y and z and momentum is P with components px, py and pz.
(b) Show that if the particle moves only in X – Y plane, the angular momentum has only a z – component?
Answer:
(a) Let OX, OY and OZ be the three mutually perpendicular, axes. Consider a particle at point P with position vector.
OP = r in X – Y plane.
Let θ = angle made by its linear momentum p with r produced. If L be its angular momentum. Then L = r × p ……………….. (i)
It is a vector quantity and its direction is given by right hand rule for vector product. As r and p here lie in XOY plane, so L acts along Z axis.
In cartesian co-ordinates,
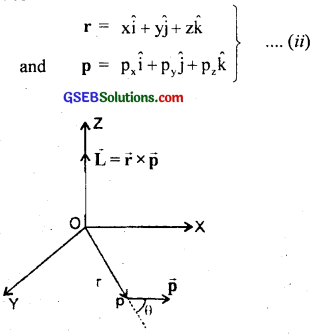
∴ From (i) and (ii) we get,

eqn. (iii) gives the required components of L along X, Y and Z axis.
(b) We know that the torque experienced by a particle moving in XY plane is given by
τz = xFy – yFx …………………… (1)
where τz = component of torque acting along Z axis on the particle moving in XY plane.
Let m = mass of the particle having its y in XY plane.
s.t. vx and vy be its velocity components along X and Y axes respectively.
∴ According to Newton’s Second law of motion,
 ……………………… (2)
……………………… (2)
∴ from (1) and (2) we get,

∴ from (3) and (4) we get,
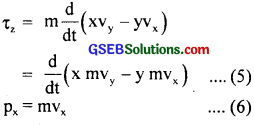
Now as py = mvy and px = mvx
∴ from (5) and (6), we get

Hence from equation (7), we conclude that a particle moving in XY plane has only one component of L i.e. Lz acting along Z-axis.
![]()
Question 7.
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the. same whatever be the point about which the angular momentum is taken?
Answer:
Here, m = mass of each particle moving along two parallel lines at a distance d from each other.
v = Speed of each particle moving in opposite directions.
Let the particles be at points P1 and P2 at some instant t.
Let we want to calculate the angular momentum of the system made by these two particles about any arbitrary point O. If L1 and L2 be the angular momenta of each particle, then
L1 = r1 × mv
and L2 = r2 × mv
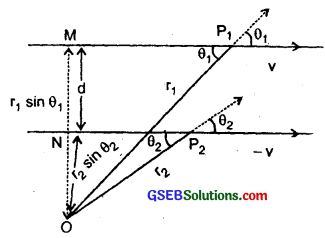
If L be the angular momentum of the system,
then L = L1 – L2
= r1 × mv – r2 × (mv)
= r1 × mv – r2 × mv
Here – ve sign has been taken as the two particles move in opposite directions.
or L = ||(L1| – |L2||
= mvr1sinθ1, – mvr2sinθ2 ……………………. (1)
where θ1 and θ2 are the angles between r1,v and r2, v respectively as shown in the figure.
Although the particles change their positions with time, the lines of direction of v remains the same and hence OM = r1sinθ1, and ON = r2sinθ2 remain constant.
Also OM – ON = d (given) = MN
i. e. r1sinθ1 – r2sinθ2 = d ………………….. (2)
∴ From (1) and (2), we get
|L| = mvd
Also the direction of L is ⊥ to the plane of r and v and is inward the plane of paper. This direction does not change with time. Thus, L remains same in magnitude and direction and is therefore conserved.
Question 8.
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in the figure. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2m long. Calculate the distance of the centre of gravity of the bar from its left end?
Answer:
Let AB be the uniform bar of weight W suspended at rest by the two strings OA and OB which make angles 36.9° and 53.1° respectively with the vertical.
∴ ∠OAA’ = 90° – 36.9° = 53.1°
Similarly ∠O’BB’ = 36.9°
AB = 2m, AC = dm.
Let T1 and T2 be the tensions in the strings OA and O’B respectively and their rectangular components are shown in the figure.
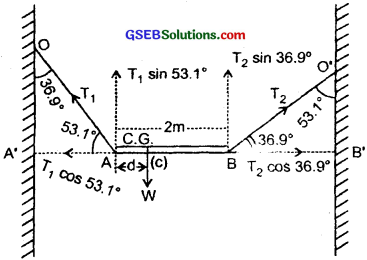
As the rod is at rest, so the vector sum of the forces acting along A’B’ axis and ⊥ to it are zero i.e.
– T1cos 53.1° + T2cos 36.9° = 0 ………………… (i)
and T1 sin53.1° + T2sin36.9°- W = 0 …………………. (ii)
Taking the torques about A and equating the sum of torques to zero, we get
– (T2sin36.9°) × 2 + Wd = 0
or T2 = \(\frac{\mathrm{Wd}}{2 \sin 36.9^{\circ}}\) ………………….. (iii)
∴ from (ii) and (iii), we get
T1sin 53.1° = W – T2 Sin 36.9°
= W – \(\frac{Wd}{2}\)
∴ T1 = \(\frac{W}{sin53.1°}\) (1 – \(\frac{d}{2}\)) ……………………. (iv)
∴ from (i), (iii) and (iv), we get
T1cos53.1° = T2cos36.9°

or d = \(\frac{1}{1.3870}\) = 0.721 m = 72.1 cm
![]()
Question 9.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel?
Answer:
Let m kg = mass of each front wheel
∴ (900 – m)kg = mass of each back wheel
∴ m × 1.05 = (900 – m) × 0.75
or 1.8 m = 900 × 0.75
or m = 375 kg
∴ 900 – m = 525 kg
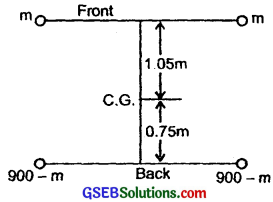
∴ weight of each front wheel, w1 = mg = 375 × 9.8 N = 3675N
weight of each back wheel, w2 = 525 × 9.8 = 5145N
∴ Force exerted by the level ground on each front wheel is the reaction of the ground = w1 = 3675N
Similarly force exerted by the level ground on each back wheel is the reaction of the ground = w2 = 5145N.
Aliter:
M = 1800 kg Let R1 and R2 be the reactions on front and back wheels.
∴ R1 + R2 = mg = 1800 × 9.8
Taking moment about C.G.,
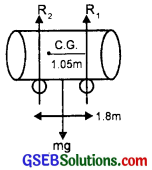
R1 × 1.05 = R2 × 0.75
or R1 = \(\frac{5}{7}\) R2
∴ \(\frac{5}{7}\) R2 + R2 = 1800 × 9.8
or R2 = 10290N
So force on each back wheel = \(\frac{10290}{2}\) = 5145N.
∴ R1 = \(\frac{5}{7}\) × 10290 = 7350
∴ Force on each front wheel = \(\frac{7350}{2}\) = 3675N.
Question 10.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the M.I. of the sphere about any of its diameter to be 2 MR2/5, where m is the mass of the sphere and R is the radius of the sphere?
(b) Given the M.I. of disc of mass M and radius R about any of its diameters to the MR2/4, find its M.I. about an axis normal to the disc and passing through a point on its edge?
Answer:
(a) Let IAB be the M.I. of the given sphere of radius R and mass m about the diameter AB
∴ IAB = \(\frac{2}{5}\) MR2 …………………… (i)
It means the sphere is solid. Let CD be a tangent of the sphere parallel to the diameter AB of the sphere.
∴ Distance between the two parallel axis is R. If ICD be its MI about CD axis, then according to the theorem of parallel axis,
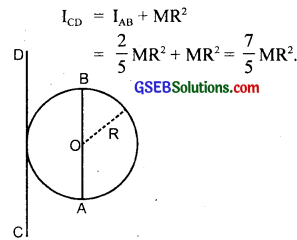
(b) Here, AB and CD are the diameters of the disc of radius R and mass M. Let EF be an axis ⊥ar to the plane of disc and passing through its C.M. i.e. O. Clearly DG is the axis normal to the disc and passing through a point D on its edge.
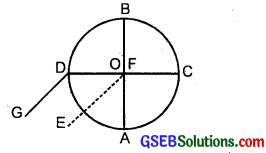
Clearly the axis DG is parallel to the axis EF.
∴ IEF = IAB + ICD
= \(\frac{\mathrm{MR}^{2}}{4}\) + \(\frac{\mathrm{MR}^{2}}{4}\) = \(\frac{1}{2}\) MR2
Here, ⊥ar distance between EF and DG axis = R
∴ If IDG be the M.I. of the disc about the required axis, then according to theorem of parallel axes,
IDG = IEF + MR2
= \(\frac{1}{2}\) MR2 + MR2 = \(\frac{3}{2}\) MR2.
![]()
Question 11.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Answer:
Let M, R be the mass and radius of the hollow cylinder and the solid sphere.
Let I1 and I2 be the moments of inertia of the hollow cylinder about its axis of symmetry and solid sphere about its axis through its centre respectively.
Then I1 = MR2 ………………. (i) [∵ 1 = \(\frac{1}{2}\)(R21 + R22)
If cylinder is hollow and thin, then R2 ~ R ~ R here
∴ I = \(\frac{1}{2}\)m × 2R = MR2]
and I2 = \(\frac{2}{5}\) MR2 ……………….. (ii)
Let τ = magnitude of the torque applied on each of them.
If α1, and α2 be the angular accelerations produced in the cylinder and sphere respectively, then
τ = I1α1
and τ = I2α2
∴ I1α1 = I2α2

= 2.5 α1 …………………. (iii)
If ω1 and ω2 be the angular speed p and sphectroc of the cylinder and sphere after a time t, then
ω1 = ω0 + α1t …………………. (iv)
and ω2 = ω0 + α2t
= ω0 + 2.5 α1t …………………. (v)
Where ω0 = initial angular speed.
∴ from (iv) and (v), it is clear that
ω2 > ω1
∴ The sphere will acquire more angular speed as compared to that of the cylinder after a given time.
Question 12.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Answer:
Here, m = 20 kg
R = 025 m
ω = 100 rads-1
If I be the M.I. of the cylinder about its axis,
then I = MR2 = \(\frac{1}{2}\) × 20 × (0.25)2
= 0.625kg m2
∴ K.E. associated with the rotating cylinder is given by
K.E. = \(\frac{1}{2}\) Iω2 = \(\frac{1}{2}\) × 0.625 × (100)2
= \(\frac{1}{2}\) × 625 × \(\frac{10^{4}}{10^{3}}\) = 3125 J
Also using the relation,
K.E. = \(\frac{{L}^{2}}{{2I}}\), we get
L2 = 2I (K.E.)
or L = \(\sqrt{2I(K.E.)}\)
= \(\sqrt{2×0.625×3125}\)
or L = \(\sqrt{\frac{(625)^{2} \times 10}{10^{3}}}\) = 62.5 Js.
![]()
Question 13.
(a) A child stands at the centre of a turn table with his two arms outstretched. The turn table is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moments of inertia to 2/5 times the initial value? Assume that the turn table rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Answer:
(a) Let I1 and I2 be the initial and final moments of inertia of the child i.e. with outstretched and folding arms respectively
∴ I2 = \(\frac{2}{5}\) I1 (Given)
v1 = 40 rev/min = \(\frac{40}{60}\) rps
v2 = ?
∴ ω1 = 2πv1 = \(\frac{2π×40}{60}\) rads-1
= \(\frac{4}{3}\) π rads-1
Let ω1 and ω2 be the angular speed of the child with outstretched and folding arms respectively.
According to the law of conservation of angular momentum, we get
I1ω1 = I2ω2

∴ frequency of revolution v2 is given by
v2 = \(\frac{\omega_{2}}{2 \pi}\) = \(\frac{10π}{3×2π}\) rps
= \(\frac{5}{3}\) × 60 rpm = 100 rev/min
∴ v2 = 100 rpm
(b) Initial K.E. of rotation = \(\frac{1}{2}\) I1ω21
New K.E. of rotation = \(\frac{1}{2}\) I2ω22

Clearly new K.E. of rotation (when child folds his hands back) is \(\frac{5}{2}\) times greater than the initial K.E. of rotation. The increase in K.E. of rotation on folding back his hands appears due to the use of child’s own internal energy i.e. muscular energy (used in folding the arms) to increase the rotational kinetic energy.
Question 14.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assuming that there is no slipping?
Answer:
Here, mass of cylinder, M = 3 kg
Radius of cylinder, R = 0.4 m
Tangential force, F = 30 N
a = ?
α = ?
If I be the M.I. of the hollow cylinder about its axis, then
I = MR2 = 3(0.4)2
= 0.48kg m2
If τ = torque acting on the cylinder, then
τ = FR = 30 × 0.4 =12 Nm
∴ α = \(\frac{τ}{1}\) = \(\frac{12}{0.48}\) = 25 rads-2
∴ a = Rα = 0.4 × 25 = 10
Aliter:
a = \(\frac{F}{m}\) = \(\frac{30}{3}\) = 10 ms-2
![]()
Question 15.
To maintain a rotor at a uniform angular speed of 206 rad s-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine? (Note uniform angular velocity in the absence of friction implied zero torque. In practice, applied torque is needed to counter frictional torque.) Assume that the engine is 100% efficient?
Answer:
Here, ω = 200 rad s-1
τ = 180 Nm
P = ?
Using the relation, P = τω, we get
P = 180 × 200 = 36000W = 36kW.
Question 16.
From a uniform disk of radius R, a circular section of radius \(\frac{R}{2}\) is cut out. The centre of the hole is at \(\frac{R}{2}\) from the centre of the original disc. Locate the centre of gravity of the resulting flat body?
Answer:
Here, radius of original disk = R
radius of removed circular section = \(\frac{R}{2}\)
If A and ‘a’ be their respective areas’ then
A = πR2
and a = π(\(\frac{R}{2}\))2 = \(\frac{\pi \mathrm{R}^{2}}{4}\)
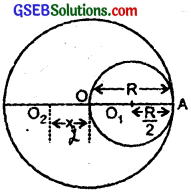
Here ‘O’ is the centre of the original disk.
and ‘O1’ is the centre of the removed circular hole.
Also let ‘O2’ = centre of the remaining portion.
p = mass per unit area of the disk.
If m1 and m be the masses of the original disc and the removed portion respectively, then
m1 = ρA = πR2ρ
and m = ρA = \(\frac{\pi \mathrm{R}^{2}}{4}\)ρ
If m2 be the mass of remaining portion, then
m2 = m1 – m
= πR2ρ – \(\frac{\pi \mathrm{R}^{2} \rho}{4}\)ρ
= \(\frac{3}{4}\) πR2ρ
Let ‘O’ be the origin.
If Rcm be the C.M. of the system made of removed and remaining portion, then
Rcm = \(\frac{\mathrm{mx}_{1}+\mathrm{m}_{2} \mathrm{x}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\) …………………. (i)
Here, x1 = OO1 = OA – O1A = R – \(\frac{R}{2}\) = \(\frac{R}{2}\)
m = \(\frac{π}{4}\) R2ρ …………………….. (ii)
m2 = \(\frac{3}{4}\)πR2ρ
x = OO2 = ?
Rcm = 0
∴ From (i) and (ii) we get,
0 = mx1 + m2x2

Here – ve sign shows that the centre of mass of the remaining portion is at \(\frac{R}{6}\) to the left side of O and opposite to the centre of removed 6 portion.
Aliter:
Let m1 and m2 be concentrated at O1 and O2 respectively, then O is their C.M. if
m × OO1 = M2 × OO2
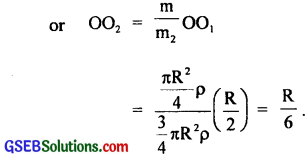
![]()
Question 17.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on top of the other at the 12cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
Answer:
Let mgm = mass/cm of the rod
If M = total mass of the metre stick, then
M = 100m gram
when it balances at the centre, then mass of each half part = 50m gram
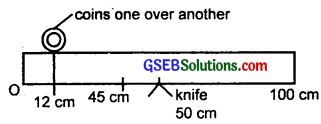
Let M = mass of two coins placed at 12cm mark
M2 = 5 × 2 = 10 gm
C.G. = at 45cm marked as A.
As the stick is in equilibrium, so the moment of different masses about point A is same i.e.
∵ 12m × 39 + 10 × 33 + 33m × \(\frac{3}{2}\) = 55m × \(\frac{55}{2}\)
or \(\frac{(55)^{2}}{2}\) m – \(\frac{(33)^{2}}{2}\) m – 12 × 39m = 330
or (3025 – 1089 – 936)m = 330 × 2 = 660
or 1000m = 660
or m = 0.66g
∴ M = 100m = 100 × 0.66 = 66g
Aliter:
Since the metre stick balances at 50cm mark,
so its C.G. must be at 50cm
Let M = mass of stick
∴ x1 = distance between 50cm mark and new C.G.
= 50 – 45 = 5cm
x2 = distance between 12cm mark and new C.G.
= 45 – 12 = 33cm
∴ for equilibrium from principle of moments,
Mg × 5 = 2 × 5 × g × 33
or M = 66g
![]()
Question 18.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination?
(a) Will it reach the bottom with the same speed in each case?
(b) Will it take longer to roll down one plane than the other?
(c) If so which one and why?
Answer:
Let θ1, l1 be the angle of inclination and distance travelled from top to bottom respectively on plane (1)
and θ2, l2 be the angle of inclination and distance travelled from top to bottom respectively on plane (2)
clearly θ1 > θ2
∴ \(\frac{\sin \theta_{1}}{\sin \theta_{2}}\) > 1 ………………… (i)
h = height of each inclined plane = l1sinθ1 = l2sinθ2
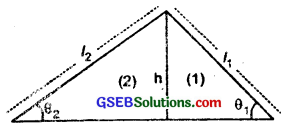
(a) Yes.
At the top of the planes, the sphere has only P.E. = mgh …………… (ii)
where m = mass of the sphere
When the sphere rolls down from the top to the bottom, P.E. is converted into K.E. of translation into K.E. of translation (\(\frac{1}{2}\)Iω2)
where I = M.I. of the sphere
v = linear speed at the bottom of the plane
ω = its angular speed
∴ If v1 and v2 be its linear speeds at the bottom of the two planes, i.e. (1) and (2) respectively, then

where K is the radius of gyration
From (ii) and (iii) it is clear that the sphere reaches the bottom with same speed in each case.
(b) To find the time of rolling motion:
Yes, it will take longer time down one plane than the other. It will be longer time down one plane having smaller angle of inclination.
(c) Explanation:
Let t1 and t2 be the time taken by the sphere in rolling on plane (1) anc (2) respectively.
Now for solid sphere

Also we know that acceleration of an object on an inclined plane is given by

where θ = angle of incline
If a1 and a2 be the accelerations of the sphere on inclined plane (1) and (2) respectively, then
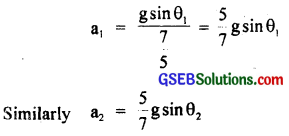
Also let t1 and t2 be the times in rolling down on the respectively planes, i.e. using the relation plane (1) and (2) respectively, then

It is due to the reason that a α sin θ and t is inversely proportional to ‘a’ or sin θ.
Question 19.
A hoop of radius 2m weighs 100 kg. It lolls along a horizontal floor so that its centre of mass has a speed of 20 cm-1. How much work has to be done to stop it?
Answer:
Here, r = 2m
m = 100 k
v = velocity of its centre of mass
u = u.20 ms-1
work done to stop it = ?
If ω be the angular velocity of the C.M. of the hoop, then
ω = \(\frac{v}{r}\) = \(\frac{0.20}{2}\) = 0.10 rads-1
Let I = M.I. of the hoop about an axis passing through its centre and ⊥ar to its plane.
∴ I = mr2 = 100 × (2)2 = 400 kg m2
∴ Total K.E. of the ring = Rotational K.E. of the hoop (i.e. ring) + Translational K.E. of the ring.

∴ According to work energy theorem,
work done to stop it = Total K.E. of the hoop = 4J.
![]()
Question 20.
The oxygen molecule has a mass of 5.30 × 10-26 kg and a moment of inertia of 1.94 × 10-46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 ms-1 and that is K.E. of rotation is \(\frac{2}{3}\) of its K.E. translation. Find the average angular velocity of the molecule?
Answer:
Here,
mass of oxygen molecule, m = 5.30 × 10-26 kg
M.I. of oxygen molecule, I = 1.94 × 10-46 kg m2
mean speed of a molecule, v = 500 ms-1
average angular speed, ω = ?
Now according to the given condition,
K.E. of rotation = \(\frac{2}{3}\) × K.E. of translation
or \(\frac{1}{2}\)Iω2 = \(\frac{2}{3}\)\(\frac{1}{2}\)mv2
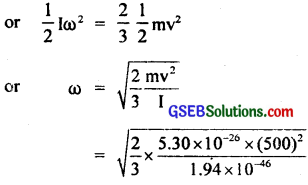
= 1.35 × 1010 × 500 rads-1
= 6.75 × 1012 rads-1.
Question 21.
A cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 ms-1.
(а) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Answer:
Here, θ = 30°
Speed of C.M. of cylinder at the bottom, u = 5 ms-1
(a) – a = acceleration in the cylinder rolling up the inclined plane

Let s = distance covered up the plane = ?
∴ v = 0
using the relation, v2 – u2 = 2as, we get
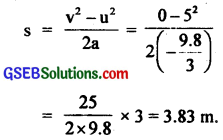
(b) Let T = time taken by the cylinder to return to the bottom = ?
T = 2t, where t = time of ascending or descending
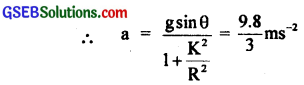
s = 3.83 m
Here initial velocity = 0
∴ using the relation, s = ut + \(\frac{1}{2}\) at2

∴ T = 2 × 1.53 = 3.06s ~ 3.0s.
Note: \(\frac{1}{2}\) mv2 + \(\frac{1}{2}\) Iω2 = mgh
or \(\frac{1}{2}\) mv2 + \(\frac{1}{2}\).\(\frac{1}{2}\) mv2ω2 = mgh
∴ x = h/sin θ.
or \(\frac{3}{4}\) mv2 = mgh
∴ h = \(\frac{3 v^{2}}{4 g}\).