Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Ex 1.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Ex 1.4
![]()
Question 1.
Determine whether or not each of the definitions of * given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z+, define * by a * b = a – b.
(ii) On Z+, define * by a * b – ab.
(iii) On R, define * by a * b = ab²
(iv) On Z+, define * by a* b = |a-b|.
(v) On Z+, define * by a * b – a.
Solution:
(i) a > b, a * b = a – b > 0 which belongs to Z+.
But if a < b, a * b = a – b < 0 which does not belong to Z+.
⇒ given operation * is not a binary operation.
(ii) For all a and b belonging to Z+, ab also belongs to Z+.
∴ The operation *, defined by a * b = ab is a binary operation.
(iii) For all a and b belonging to R, ab² also belongs to R.
⇒ The operation *, defined by a * b = ab² is a binary operation.
(iv) For all a and b belonging to Z+, |a – b| also belongs to Z+.
∴ The operation a * b = |a-b| is a binary operation.
(v) On Z+, defined by a * b = a,
a, b ∈ Z+ ⇒ a ∈ Z+.
∴ is a binary operation.
![]()
Question 2.
For each binary operation * defined below, determine whether * is commutative or associative:
(i) On Z, define a * b = a – b.
(ii) On Q, define a * b = ab + 1.
(iii) On Q, define a * b = \(\frac { a }{ 2 }\)
(iv) On Z+ define a * b = 2a
(v) On Z+, define a * b = ab
(vi) On R – {-1}, define a * b = \(\frac { a }{ b+1}\)
Solution:
(i) On Z, operation * is defined as
(a) a * b = a – b
⇒ b * a = b – a
But a – b + b – a ⇒ a * b # b * a
(b) a – (b – c) * (a-b)-c
Binary operation defined as # is not associative.
(ii) On Q, operation * is defined as a * b = ab + 1.
(a) ab + 1 = ba + 1, a * b = b * a
∴ Defined binary operation is commutative.
(b) a* (b * c) = a * (bc + 1) = a(bc + 1) + 1 = abc + a + 1
and (a * b) * c = (ab + 1) * c = (ab + 1)c + 1
= abc + c + 1
⇒ a * (b * c) # (a * b) * c
∴ Binary operation defined as * is not associative.
(iii) (a) On Q, operation * is defined as a * b = \(\frac { ab }{ 2 }\)
∴ a * b = b * a
∴ Operaion binary defined as * is commutative.
(b) a * (b * c) = a* \(\frac { bc }{ 2 }\) = \(\frac { abc }{ 2 }\).
and (a * b) * c = \(\frac { ab }{ 2 }\) * c = \(\frac { abc }{ 4 }\).
⇒ Defined binary operation * is associative.
(iv) On Z+, operation * is defined as a * b = 2ab
(a) a * b = 2ab, b * a = 2ab = 2ab
⇒ a * b = b * a
∴ Binary operation defined as * is commutative.
(b) a * (b * c) = a * 2ab = 2a.2b
(a * b) * c = 2ab * c = 22ab
Thus, (a * b) * c ≠ a * (b * c).
∴ Binary operation defined as * is not associative.
(v) On Z+, a * b = ab
(a) b * a = ba
∴ ab ≠ ba ⇒ a * b # b * a
* is not commutative.
(b) (a * b) * c = ab * c = (ab)c = abc
a * (b * c) = a * bc = abc
Thus, (a * b) * c # (a * b * c)
∴ Operation * is not associative.
(vi) On Z+, operation * is defined as
a + b = \(\frac { a }{ b+1 }\), b # 1
∴ b * a = \(\frac { b }{ a+1 }\)
(a) a * b * b * a
Binary operation defined above is not commutative.

⇒ Binary operation defined above is not associative.
![]()
Question 3.
Consider the infimum binary operation Λ on the set {1, 2, 3, 4, 5} defined by a Λ b = min of a and b. Write the multiplication table of the operation Λ.
Solution:
Operation A table on the set (1, 2, 3, 4, 5} is as follows:

Question 4.
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table:

(i) Compute (2 * 3) * 4 and 2 * (3 * 4).
(ii) Is * commutative?
(iii) Compute (2 * 3) * (4 * 5).
Solution:
(i) From the table given above, we find:
2 * 3 = 1, 1 * 4 = 1
(a) (2 * 3) * 4 = 1 * 4 = 1.
(b) 2 * (3 * 4) = 2 * 1 = 1.
(ii) Let a, b ∈ {1, 2, 3, 4, 5}
From the given table, we find:
a * a = a,
a * b = b * a = 1, when a or b or both odd and a≠b.
2 * 4 = 4 * 2 = 2, when a and b are even and a≠b.
Thus, a * b = b * a
∴ Given binary operation * is commuative.
(iii) (2 * 3) * (4 * 5) = 1 * 1 = 1.
Question 5.
Let *’ be the binary operation on the set {1, 2, 3, 4, 5}, defined by a *’ b = HCF of a and b. Is.the operation *’ same as operation * defined in quesion 4 above? Justify your answer.
Solution:
The set is {1, 2, 3, 4, 5} and a *’ b = HCF of a and b.
Let us prepare the table of operaion *’:
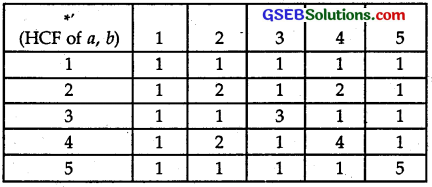
This table is the same as given in Question 4.
∴ Operations *’ and * (as defined in Question No. 4) are the same.
Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b.
(i) Find 5 * 7 and 20 * 16.
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N.
(v) Which elements of N are invertible for the operation *?
Solution:
Binary operation * defined as a * b = L.C.M. of a and b.
(i) 5 * 7 = L.C.M. of 5 and 7 = 35.
20 * 16 = L.C.M. of 20 and 16 = 80.
(ii) a * b = L.C.M. of a and b
b * a = L.C.M. of b and a
= a * b = b * a, since L.C.M. of a, b and b, a are equal.
Binary operation * is commutative.
(iii) a * (b * c) = L.C.M. of a, b, c
and (a * b) * c = L.C.M. of a, b, c
⇒ a * (b * c) = (a * b) * c
⇒ Given binary operation * is associative.
(iv) Identity of * in N is 1 because
1 * a = a * 1 = a = L.C.M. of 1 and a.
(v) Let * : N x N → N defined as a * b = L.C.M. of (a, b)
For a = 1, b = 1, a * b = 1 = b * a. Otherwise a * b * 1.
∴ Binary operation * is not invertible.
⇒ 1 is invertible for operation *.
Question 7.
Is * defined on the set {1,2,3,4,5} by a * b = L.C.M. of a and b as a binary operation. Justify your answer.
Solution:
The given set = {1, 2, 3, 4, 5}.
Binary operation * is defined as a * b = L.C.M. of a and b.
4 * 5 = 20 which does not belong to the given set {1, 2, 3, 4, 5}. So, it is not a binary operation.
![]()
Question 8.
Let * be the binary operation of N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does their exist identity for this operation on N?
Solution:
Binary operation on set N is defined as
a * b = H.C.F. of a and b.
(a) We know that H.C.F. of a, b = H.C.F. of b, a.
∴ a * b = b * a
Binary operation * is commutative.
(b) a * (b * c) = a * (H.C.F. of b, c)
= H.C.F. of a and (H.C.F. of b, c)
= H.C.F. of a, b and c.
Similarly, (a * b) * c = H.C.F. of a, b and c
⇒ (a * b) * c – a * (b * c)
So, binary operation * as defined above is associative.
(c) 1 * a = a * 1 = 1 * a.
There does not exists any identity element.
Question 9.
Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a – b
(ii) a * b = a² + b²
(iii) a * b = a + ab
(iv) a * b = (a – b)²
(v) a * b = \(\frac { ab }{ 4 }\)
(vi) a * b = ab²
Find which of the above binary operations are commutative and which are associative.
Solution:
Operation * is on the set Q.
(i) Defined as a * b = a – b
(a) Now b * a = b – a. But a – b ≠ b – a
∴ a * b ≠ b * a
∴ Operation * is not commutative.
(b) a * (b * c) = a * (b-c)
= a – (b-c)
= a – b + c
(a * b) * c = (a – b) * c
= a – b – c
Thus a * (b * c) ≠ (a * b) * c
The operation *, as defined above is not associative.
(ii) (a) a * b = a² + b²
b * a = b² + a² = a² + b²
∴ a * b = b * a
∴ This binary operation * is commutative.
(b) a * (b * c) = a * (b² + c²) = a² + (b² + c²)²
(a * b) * c = (a² + b²) * c = (a² + b²) + c²
⇒ a * (b * c) ≠ (a * b) * c
∴ The given operation * is not associaive.
(iii) Operation * is defined as a * b = a + ab
(a) b * a = b + ba
∴ a * b = b * a
∴ This operation * is not commutative.
(b) a * (b * c) = a * (b + bc)
= a + a(b + be)
= a +ab + abc
(a * b) * c = (a + ab) * c
= a + ab + (a + ab).c
= a + ab + ac + abc
⇒ a * (b * c) # (a * b) * c
⇒ The given binary operation * is not associative.
(iv) The binary operation * is defined as
a * b = (a – b)²
(a) b * a = (b – a)² = (a – b)²
⇒ a * b = b * a
This binary operation * is commutative.
(b) a * (b * c) = a * (b – c)²
= [a – (b – c)²]²
(a * b) * c = (a – b)² * c
= [(a-b)²-c]²
⇒ a * (b * c) # (a * b) * c
∴ The operation * is not associative.
(v) Binary operaion * is defined as
a * b = \(\frac { ab }{ 4 }\)
∴ The operation * is commutative.
(b) a * (b * c) = a * \(\frac { ab }{ 4 }\) = \(\frac { a }{ 4 }\)( \(\frac { bc }{ 4 }\)) = \(\frac { abc }{ 16 }\)
(a * b) * c = \(\frac { ab }{ 4 }\) * c = \(\frac { ab }{ 4 }\) * c = \(\frac { ab }{ 4 }\).\(\frac { c }{ 4 }\) = \(\frac { abc }{ 16 }\)
⇒ (a * b) * c = a * (b * c)
Thus, the given operation * is associative.
(vi) Binary operation * is defined as
a * b = ab²
(a) b * a = ba² ≠ ab²
∴ a * b * b * a.
∴ The operation * is not commuative.
(b) a * (b * c) = a * bc² = a(bc²)² = abc²
(a * b) * c = ab² *c = (ab²)c² = ab²c²
∴ a * (b * c) * (a * b) * c.
∴ Given binary operation * is not associative.
![]()
Question 10.
Show that none of the operations given above has identity.
Solution:
The binary operation * on set Q is
(i) defined as a * b = a – b.
For idenity element e, a * e = e * a = a.
But a * e = a – e # a and e * a = e – a # a.
∴ There is no identity element for this operation.
(ii) Binary operation * is defined as
a * b = a² + b²
Here, a * e = a² + e² # a
and e * a – e² + a² # a.
So, this operation * has no identity.
(iii) The binary operation * is defined as
a * b = a + ab
We have: a * e = a + ae # a
and e * a = e + ea # a.
∴ There is no identity element.
(iv) The binary operation * is defined as
a * b = (a – b)²
Put b = e. We get a * e = (a – e)² # a
and e * a = (e – a)² # a
for any value of e ∈ Q.
⇒ There is no identity element.
(v) The operation * is
a * b = \(\frac { ab }{ 4 }\).
and e * a = \(\frac { ab }{ 4 }\) # a
for any value of e ∈ Q.
∴ Operation * has no identity element.
(vi) The operation * is a * b = ab².
Put b = e. We get a * e = ae² # a
and e * a = ea² # a
for any value of e ∈Q.
⇒ There is no identity element.
Thus, these operations have no identity.
Question 11.
Let A = N x N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d).
Show that * is commutative and associative. Find the identity for * oh A, if any.
Solution:
A = N x N
Binary operation * is defined as
(a, b) * (c, d) = (a + c, b + d).
(a) Now, (c, d) * (a, b) = (c + a, d + b)
= (a + c, b + d)
⇒ (a, b) * (c, d) = (c, d) * (a, b)
∴ This operation * is commutative.
(b) Next
(a, b) * [(c, d) * (e, f)] = (a, b) * (c + e, d + f)
= [(a + c + e), (b + d + f)]
and
[(a, b) * (c, d)] * (e, f) = (a + c, b + d) * (e, f)
= [(a + c + e), (b + d + f)]
⇒ (a, b) * [(c, d) * (e, f) = [(a, b) * (c, d)] * (e, f)
∴ The given binary operation is associative.
(c) Identity element does not exist, because there is no e and e’ in N x N such that (a, b) * (e, e’) = (a + e, b + e’) = (a, b).
![]()
Question 12.
State whether the following statements are true or false. Justify.
(i) For any arbitrary binary operation * on a set N,
a * a = a ∀a ∈ N.
(ii) If * is commutative binary operation on N, then a * (b * c) = (c * b) * a.
Solution:
(i) A binary operation on N is defined as
a * a = a ∀a ∈ N.
Here, operation * is not defined.
∴ Given statement is false.
(ii) * is a binary commutative operation on N.
⇒ c * b = b * c [∵ * is commutative]
∴ (c * b) * a = (b * c) * a = a * (b * c)
∴ a * (b * c) = (c * b) * a.
∴ This statement is true.
Question 13.
Consider a binary operation * on N defined as
a * b = a³ +b³. Choose the correct answer:
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution:
The binary operation * on set N is defined as
a * b = a³ +b³
Now, b * a = b³ + a³ = a³ +b³.
⇒ a * b = b * a.
∴ The operation * is commutative.
Further, a * (b * c) = a * (b³ + c³) = a³ + (b³ + c³)³
and (a * b) * c = (a³ + b³) * c = (a³ +b³)³ + c³
⇒ a * (b * c) ≠ (a * b) * c
∴ This operation is not associative.
Thus, this operation is commutative but not associative.
Part (B) is the correct answer.