GSEB Solutions Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise

Question 1.
Let R → R be defined as f(x) = 10x + 7. Find the function g : R → R such that gof = fog = I_R.
Solution:
Let f : X → Y, where X ⊆ R, Y ⊆ R.
Consider an arbitrary element y of Y.
By definition, y = 10x + 7 for some x ∈ X.
⇒ x = \(\frac { y-7 }{ 10 }\).
Let us define g : Y → X by g(y) = \(\frac { y-7 }{ 10 }\)
= \(\frac { (10x+7)-7 }{ 10 }\) = x
Now gof(x) = g[f(x)] = \(\frac { f(x)-7 }{ 10 }\)
= \(\frac { (10x+7)-7 }{ 10 }\)
and fog(x) = f[g(x)] + 10g(y) + 7 = 10.\(\frac { y-7 }{ 10 }\) + 7 = y.
⇒ gof(x) = I_R, fog(y) = I_R
⇒ f is invertible and g : Y → X, such that g(y) = \(\frac { y-7 }{ 10 }\).

Question 2.
Let f : W → W be defined as f(n) = n -1, if n is odd and f(n) = n + 1, if n is even. Show that/is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Solution:
We are given, f : W → W, defined as
\(\left\{\begin{array}{ll} n-1, & n \text { is odd } \\ n+1, & n \text { is even } \end{array}\right.\)
Let f(n₁) =f(n₂). If n₁ is odd and n₂ is even,
then n₁ – 1 = n₂ + 1, i.e., n₁ – n₂ = 2, which is not possible as n₁ is odd and n₂ is even.
When n₁ and n₂ both are odd, then
f(n₁) =f(n₂) ⇒ n₁ – 1 = n₂ – 1 ⇒ n₁ = n₂
When n₁ and n₂ both are even
f(n₁) = f(n₂) ⇒ n₁ + 1 = n₂ + 1 ⇒ n₁ = n₂.
This shows f is one-one.
Any odd number 2r + 1 in codomain is the image of 2r and any even number 2r in the codomain W is the image of 2r + 1.
⇒ f is one-one and onto.
∴ f is invertible.
Further, when n is odd, y = n – 1, n = y + 1, y is even.
When n is even, y = n + l, n = y y is odd.
Hence, f^-1(y) = g(y) defined as
g : W → W, such that g(y) = \(\left\{\begin{array}{ll}
y-1, & y \text { is odd } \\
y+1, & y \text { is even }
\end{array}\right.\)
⇒ The inverse of f is f itself.

Question 3.
If f : R → R is defined by f(x) = x² – 3x + 2, find f[f(x)].
Solution:
f(x) = x² – 3x + 2
f[f(x)] = [f(x)]² – 3[f(x)] + 2
= (x² – 3x + 2)² – 3(x² -3x + 2) + 2
= (x⁴ + 9x² + 4 – 6x³ – 12x + 4x²) – 3x² + 9x – 6 + 2
= x⁴ – 6x³ + 10x² – 3x.

Question 4.
Show that the function f : R → { x ∈ R : – 1 – x < 1} defined by f(x) = \(\frac{x}{1+|x|}\) x ∈ R is one-one and onto. Solution: (i) Let x >0, f(x) = \(\frac { x }{ 1+x }\)
So, f(x₁) = f(x₂)
⇒ \(\frac{x_{1}}{1+x_{1}}\) = \(\frac{x_{2}}{1+x_{2}}\)
or x₁(1 + x₂) = x₂(1 + x₁)
or x₁ + x₁x₂ = x₂ + x₁x₂
⇒ x₁ = x₂
When x< 0, f(x) = \(\frac { x }{ 1-x }\)
So, f(x₁) = f(x₂)
⇒ \(\frac{x_{1}}{1-x_{1}}\) = \(\frac{x_{2}}{1-x_{2}}\)
or x₁(1 – x₂) = x₂(1 – x₁)
or x₁ – x₁x₂ = x₂ – x₂x₁
⇒ x₁ = x₂

(ii) As -1 < x < 1, f(x) = \(\frac{x}{1+|x|}\) lies between and – \(\frac { 1 }{ 2 }\) and \(\frac { 1 }{ 2 }\) When x >0, y = \(\frac { x }{ 1+x }\).
∴ (1 + x)y = x
or xy – x = – y
∴ x(y-1) = – y
or x = \(\frac { -y }{ y-1 }\) = \(\frac { 1 }{ 1-y }\).
When x < 0, f{x) = \(\frac { x }{ 1-x }\) = y
∴ x = y – xy
x(1 + y) = y
∴ x = \(\frac { y }{ 1+y }\)
In both cases, each value of y in codomain of f has a unique value in its domain.
Hence, f is onto.
Thus, f is one-one and onto.

Question 5.
Show that the function f : R → R given by f(x) = x³ is injective.
Solution:
f(x) = x³
⇒ f(x₁) = f(x₂)
⇒ x³₁ = x³₁
⇒ x₁ = x₂
⇒ f is one-one, i.e., f is injective.

Question 6.
Give examples of two functions f : N → Z and g : Z → Z such that gof is injective but g is not injective.
Solution:
Example:
(i) Let f(x) = x
and g(x) = | x |.
Consider g(x) = | x | ⇒ g is not injective,
since – 1 and 1 have the same image 1.
But (gof) (x) = g[f(x)] = g(x) = | x |
But domain of gof is N.
For every natural number n, | n | = n, n ∈ N, gof has a unique image.
∴ gof is injective.

(ii) f(x) = 2x
and g(x) = x².

Question 7.
Give examples of two functions f : N → N and g : N → N such that gof is onto but f is not onto.
Solution:
Example:
(i) Let f(x) = x + 1
and g(x) = \(\left\{\begin{array}{cl}
x-1 & \text { if } x>1 \\
1 & \text { if } x=1
\end{array}\right.\)
Let f(x) = y – x + 1
∴ x = y – 1.
For y = 1, x = 0 (Not a natural number)
⇒ Function/is not onto.
When x > 1 ,(gof)(x) = g[f(x)] = g(x +1) = x + 1 – 1 = x
This is the identity function.
Hence, it is an onto function.

(ii) Let f(x) = x + 2
and g(x) = \(\left\{\begin{array}{cl}
x-2, & \text { if } x>2 \\
2, & \text { if } x=2
\end{array}\right.\)

Question 8.
Given a non-empty set X, consider P(X) which is the set of all such sets of X. Define the relation R in P(X) as follows:
For subsets A, B in P(X), ARB if and only if A ⊂ B. Is R an equivalence relation on P(X)? Justify your answer.
Solution:
(i) A⊂A ⇒ R is reflexive.
(ii) A ⊂ B, B ⊂ A ∴ R is not symmetric.
(iii) If A ⊂ B, B ⊂ C, then A ⊂ C ∴ R is transitive.
⇒ R is not an equivalence relation.

Question 9.
Given a non-empty set X, consider the binary operaion * : P(X) x P(X) → P(X), given by A * B = A ∩ B, for all A, B in P(X), where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation *.
Solution:
We have * : P(X) x P(X) → P(X)
given by A* B = A ∩B
∴ X * A = X ∩ A = A * X = A for all A.
∴ X is an identity element.
Let I is an other identity
⇒ I ∩ A = A ∩ I = A for all A
and x ∈ X, I ∩ {x} = {x}
x ∈ I ⇒ X ⊂ I and I ⊂ X
⇒ I = X.

Question 10.
Find the number of all the onto functions from the set {1, 2, 3, …,n } to itself.
Solution:
Let
Y: 1 2 3 4 …. n
X: 1 2 3 4 …. n
One of the elements of set Y (say 1) may have any one of the pre-images 1, 2, 3, … n, i.e., in n ways.
The second element say 2 will have the pre-image in (n – 1) ways.
∴ The number of ways, we can have the pre-images
n x (n – 1)(n – 2) …. 3. 2. 1 = n!
Thus, there are nl possible onto functions.
∈
Question 11.
Let S = {a, b, c] and T = {1, 2, 3}. Find F^-1 of the following functions F from S to T₁, if it exists:
(i) F = {(a, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
Solution:
S = {a, b, c} and T = {1, 2, 3}
(i) F = [(a, 3), (b, 2), (c, 1)}
i.e., F(a) = 3, F(b) = 2, F(c) = 1
⇒ F^-1(3) = a, F^-1(2) = b, F^-1(1) = c
F^-1 = {(3, a), (2, b), (1, c)}

(ii) F = {(a, 2), (b, 1), (c, 1)}
F is not one-one since elements b and c have the same image I.
∴ It is not a one-one function. So, its inverse does not exist.

Question 12.
Consider the binary operations *: R x R → R and o: R x R → R defined as a * b = |a-b| and a o b = a for all a, b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that for all a, b, c ∈ R:
a * ( b o c) = (a * b) o (a * c)
[If it is so, we say that operation * distributes over the operation o]. Does o distributes over *? Justify your answer.
Solution:
We have: a * b = | a – b | and a o b = a.
(i) (a) a * b = | a – b |
and b * a = | b – a | = | a – b |
⇒ Operation * is commutative.

(b) (a * b) * c = | a – b | * c = || a-b | – c |
and a * (b * c) = a * | b – c | = |a- |b – c |
Clearly, ||a – b | – c | ≠ |a – |b – c||
⇒ Operation * is not associative.

(ii) (a) a o b = a, b o a = b.
Thus, a o b ≠ ⇒ b o a
⇒ Operation o is not commutative.

(b) (a o b) o c = a o c = a
and a o (b o c) = a o b = a
⇒ Operation o is associative.

(iii) For a * (b o c) = (a * b) o (a * c):
L.H.S. = a * (b o c) = a * b [∵ b o c = b]
= | a – b |

R.H.S. = (a * b) o (a * c)
= | a -b | o | a – c | = | a – b |
⇒ L.H.S. = R.H.S.
Hence, verified,
i.e., a * (b o c) = (a * b) o (a * c)

(iv) a o (b * c) = (a o b) * (a o c)
L.H.S. = a o (b * c) = a o | b – c | = a.
R.H.S. = (a o b) * (a * c) = a * a
= | a – a | = 0.
⇒ L.H.S. ≠ R.H.S.
o is not distributive over *.

Question 13.
Given a non-empty set X, let * : P(X) x P(X) → P(X) be defined as A * B = (A – B) ∪ (B – A) for all A, B ∈ P(X). Show that emptry set Φ is the identity for the operation * and all the elements of P(X) are invertible with A^-1 = A.
Solution:
Φ is the empty set.
The operation * is defined as
A * B = (A – B) ∪ (B-A)
Putting B = Φ, we get
A * Φ = (A – Φ) ∪ (Φ – A) = A ∪ Φ = A
Φ * A = (Φ – A) ∪ (A – Φ) = Φ ∪ A = A
⇒ A * Φ = Φ * A
Also, A * A = (A – A) ∪ (A – A) = Φ ∪ Φ = Φ
⇒ is an identity element.
Also, A * A = Φ ⇒ A^-1 = A.

Question 14.
Define a binary operation * on the set {0, 1, 2, 3, 4, 5} as
a * b = \(\left\{\begin{array}{cl} a+b, & \text { if } a+b<6 \\ a+b-6, & \text { if } a+b \geq 6 \end{array}\right.\)
Show that 0 is the identity for this operation and each element of the set is invertible with 6 – a being the inverse of a.
Solution:
(i) e is the identity element, if a * e = e * a = a.
a * 0 = a + 0, 0 * a = 0 + a = a.
⇒ a * 0 = 0 * a = a.
∴ 0 is the identity for the operation.

(ii) b is the inverse of a if a * b = b * a = e.
Now, a * (6 – a) = a + (6 – a) – 6 = 0
and (6 – a) * a = (6 – a) + a – 6 = 0.
Hence, each element of a of the set is invertible with inverse 6 – a.

Question 15.
Let A = {-1, 0, 1, 2}, B = {- 4, – 2, 0, 2} and/and g: A → B be functions defined by f(x) = x² – x, x ∈ A and g(x) = 2 |x – \(\frac { 1 }{ 2 }\)| – 1, x ∈ A. Are f and g equal? Justify your answer.
Solution:

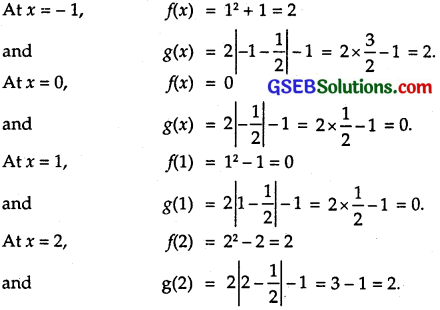
Thus, for each a ∈ A, f(a) = g(a).
⇒ f and g are equal functions.

Question 16.
Let A = {1,2,3}. Then, the number of relations containing {1, 2} and {1, 3} which are reflexive, symmetric but not transitive are
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
There is only one relation containing (1, 2) and (1, 3), which is reflexive and symmetric but not transitive is {1, 1}.
Part (A) is the correct answer.

Question 17.
Let A = {1, 2, 3}. Then, number of equivalence relations containing (1, 2) is
(A) 1
(B) 2
(C) 3
(D) 4
Solution:
There are two equivalence relations containing (1, 2).
Part (B) is the correct answer.

Question 18.
Let f : R → R be the Signum Function defined as
f(x) = \(\left\{\begin{array}{ll}
1, & x>0 \\
0, & x=0 \\
-1, & x<0
\end{array}\right.\)
and g : R → R be the greatest Integer Function given by g(x) = | x |, where | x | is the greatest integer less than or equal to x. Then, does f o g and g o f coincide in (0,1].
Solution:
f : R → R, the Signum Function is defined as
f(x) = \(\left\{\begin{array}{ll}
1, & x>0 \\
0, & x=0 \\
-1, & x<0
\end{array}\right.\)

Question 19.
Number of binary operations on the set (1, 2} having 1 as the identity element is
(A) 10
(B) 16
(C) 20
(D) 8
Solution:
Let * be a binary operation.
There are two elements in the set {1, 2}.
∴ Number of binary operations is 2⁴ = 16.
Part (B) is the correct answer.