Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Ex 10.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 10 Vector Algebra Ex 10.4
Question 1.
Find |\(\vec{a}\) × \(\vec{b}\)|, if \(\vec{a}\) = \(\hat {i} \) – 7\(\hat {j} \) + 7\(\hat {k} \)
and \(\vec{b}\) = 3\(\hat {i} \) – 2\(\hat {j} \) + 2\(\hat {k} \).

= (- 14 + 14)\(\hat {i} \) – (2 – 21)\(\hat {j} \) + (- 2 + 21)\(\hat {k} \)
= – (- 19)\(\hat {j} \) + 19\(\hat {k} \) = 19\(\hat {j} \) + 19\(\hat {k} \)
|\(\vec{a}\) × \(\vec{b}\)| = \(\sqrt{(19)^{2}+(19)^{2}}\) = 19\(\sqrt{1+1}\) = 19\(\sqrt{2}\).
![]()
Question 2.
Find a unit vector perpendicular to each of the vectors \(\vec{a}\) + \(\vec{b}\) and \(\vec{a}\) – \(\vec{b}\), where
\(\vec{a}\) = 3\(\hat {i} \) + 2\(\hat {j} \) + 2\(\hat {k} \) and \(\vec{b}\) = \(\hat {i} \) + 2\(\hat {j} \) – 2\(\hat {k} \).
Solution:
We have:
\(\vec{a}\) = 3\(\hat {i} \) + 2\(\hat {j} \) + 2\(\hat {k} \) and \(\vec{b}\) = \(\hat {i} \) + 2\(\hat {j} \) – 2\(\hat {k} \).
∴ \(\vec{a}\) + \(\vec{b}\) = (3 + 1)\(\hat {i} \) – (2 + 2)\(\hat {j} \) + (2 – 2)\(\hat {k} \)
= 4\(\hat {i} \) + 4\(\hat {j} \)
∴ \(\vec{a}\) – \(\vec{b}\) = (3 – 1)\(\hat {i} \) + (2 – 2)\(\hat {j} \) + (2 + 2)\(\hat {k} \)
= 2\(\hat {i} \) + 4\(\hat {k} \)
Now, (\(\vec{a}\) + \(\vec{b}\)) × (\(\vec{a}\) – \(\vec{b}\))

= (16 – 0)\(\hat {i} \) – (16 – 0)\(\hat {j} \) + (0 – 8)\(\hat {k} \)
= 16\(\hat {i} \) – 16\(\hat {j} \) – 8\(\hat {k} \).
∴ A unit vector perpendicular to both the vectors (\(\vec{a}\) + \(\vec{b}\)) and (\(\vec{a}\) – \(\vec{b}\)) is given by

Question 3.
If a unit vector \(\vec{a}\) makes angle \(\frac{π}{3}\) with \(\hat {i} \), \(\frac{π}{4}\) with \(\hat {j} \)
and an acute angle θ with \(\hat {k} \), then find θ and hence the components of \(\vec{a}\).
Solution:
Let \(\vec{a}\) = a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {k} \)
such that |a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {k} \)| = 1.
As per question:
(a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {j} \)).\(\hat {i} \) = |\(\vec{a}\)| |\(\hat {i} \)|cos \(\frac{π}{3}\)
⇒ (a1) (1) = (1)(1) × \(\frac{1}{2}\)
⇒ a1 = \(\frac{1}{2}\)
Also (a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {k} \)). \(\hat {j} \)
= |\(\vec{a}\)| |\(\hat {i} \)| cos \(\frac{π}{3}\)
⇒ (a1)(1) = (1)(1) × \(\frac{1}{\sqrt{2}}\) ⇒ a2 = \(\frac{1}{\sqrt{2}}\).
As |\(\vec{a}\)| = 1, therefore \(a_{1}^{2}+a_{2}^{2}+a_{3}^{2}\) = 1

![]()
Question 4.
Show that (\(\vec{a}\) – \(\vec{b}\)) × (\(\vec{a}\) + \(\vec{b}\)) = 2(\(\vec{a}\) × \(\vec{b}\)).
Solution:
(\(\vec{a}\) – \(\vec{b}\)) × (\(\vec{a}\) + \(\vec{b}\))
= \(\vec{a}\) × \(\vec{a}\) + \(\vec{a}\) × \(\vec{b}\) – \(\vec{b}\) × \(\vec{a}\) – \(\vec{b}\) × \(\vec{b}\)
= \(\vec{a}\) × \(\vec{b}\) + \(\vec{a}\) × \(\vec{b}\) = 2(\(\vec{a}\) × \(\vec{b}\)).
[∵ \(\vec{a}\) × \(\vec{a}\) = \(\vec{b}\) × \(\vec{b}\) = \(\vec{0}\)
and – \(\vec{b}\) × \(\vec{a}\) = \(\vec{b}\) × \(\vec{b}\)]
Question 5.
Find λ and µ, if (2\(\hat {i} \) + 6\(\hat {j} \) + 27\(\hat {k} \)) × (\(\hat {i} \) + λ\(\hat {j} \) + µ\(\hat {k} \)) = \(\vec{0}\)
Solution:
(2\(\hat {i} \) + 6\(\hat {j} \) + 27\(\hat {k} \)) × (\(\hat {i} \) + λ\(\hat {j} \) + µ\(\hat {k} \)) = \(\vec{0}\)

⇒ (6µ – 27λ)\(\hat {i} \) – (2µ – 27)\(\hat {j} \) + (2λ – 6)\(\hat {k} \) = \(\vec{0}\)
Comparing, we have:
6µ – 27λ = 0 ………………….. (1)
2µ – 17 = 0 ⇒ µ = \(\frac{27}{2}\) …………………. (2)
and 2λ – 6 = 0 ⇒ λ = \(\frac{6}{2}\) = 3 …………………. (3)
Putting for λ, µ in (1), We see that it is satisfied as
6(\(\frac{27}{2}\)) – 27(3) = 81 – 81 = 0
Hence, λ = 3 and µ = \(\frac{27}{2}\).
![]()
Question 6.
Given that \(\vec{a}\).\(\vec{b}\) = 0 and \(\vec{a}\) × \(\vec{b}\). What can you conclude about the vectors a and b?
Solution:
Given \(\vec{a}\).\(\vec{b}\) = 0 and \(\vec{a}\) × \(\vec{b}\) = \(\vec{0}\).
⇒ (\(\vec{a}\) = 0 or \(\vec{b}\) = \(\vec{0}\) or \(\vec{a}\) ⊥\(\vec{b}\)) and (\(\vec{a}\) = \(\vec{0}\) or \(\vec{b}\) = \(\vec{0}\) or \(\vec{a}\) || \(\vec{b}\))
⇒ Either \(\vec{a}\) = 0 or \(\vec{b}\) = \(\vec{0}\)
⇒ [∵ \(\vec{a}\) ⊥ \(\vec{b}\) and \(\vec{a}\) || \(\vec{b}\) can never hold simultaneously.
Question 7.
Let the vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are given as a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {k} \),
b1\(\hat {i} \) + b2\(\hat {j} \) + b3\(\hat {k} \) and c1\(\hat {i} \) + c2\(\hat {j} \) + c3\(\hat {k} \).
Thus, show that \(\vec{a}\) × (\(\vec{b}\) + \(\vec{c}\)) = \(\vec{a}\) × \(\vec{b}\) + \(\vec{a}\) × \(\vec{c}\).
Solution:
\(\vec{b}\) + \(\vec{c}\) = (b1\(\hat {i} \) + b2\(\hat {j} \) + b3\(\hat {k} \)) + (c1\(\hat {i} \) + c2\(\hat {j} \) + c3\(\hat {k} \))
= (b1 + c1)\(\hat {i} \) + (b2 + c2)\(\hat {j} \) + (b3 + c3)\(\hat {k} \)
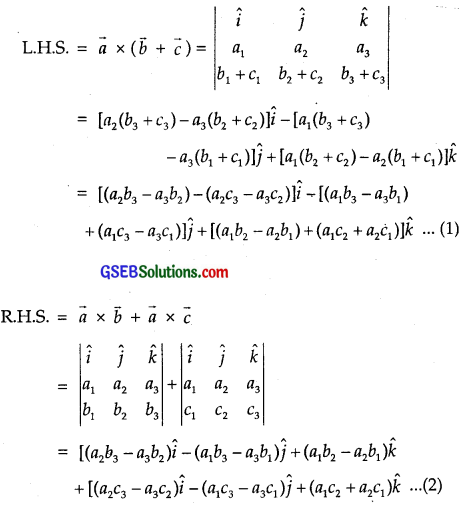
From (1) and (2), we conclude that
\(\vec{a}\) × (\(\vec{b}\) + \(\vec{c}\)) = \(\vec{a}\) × \(\vec{b}\) + \(\vec{a}\) × \(\vec{c}\).
![]()
Question 8.
If either \(\vec{a}\) = \(\vec{0}\) or \(\vec{b}\) = \(\vec{0}\), then \(\vec{a}\) × \(\vec{b}\) = \(\vec{0}\). Is the converse true?
Justify your answer with an example.
Solution:
We have:
\(\vec{a}\) = \(\vec{0}\) ⇒ |\(\vec{a}\)| = 0
∴ \(\vec{a}\) × \(\vec{b}\) = |\(\vec{a}\)| |\(\vec{b}\)| sin θ \(\hat {n} \),
where θ is the angle between \(\vec{a}\) and \(\vec{b}\).
= 0 × |\(\vec{b}\)| sin θ = 0
Similarly, when \(\vec{b}\) = \(\vec{0}\) ⇒ |\(\vec{b}\)| = 0, \(\vec{a}\) × \(\vec{b}\) = 0
Converse : Let \(\vec{a}\) = a1\(\hat {i} \) + a2\(\hat {j} \) + a3\(\hat {k} \)
and \(\vec{b}\) = pa1\(\hat {i} \) + pa2\(\hat {j} \) + pa3\(\hat {k} \).
i.e. \(\vec{a}\) and \(\vec{b}\) are parallel, So θ = 0.
and |\(\vec{a}\)| ≠ 0, |\(\vec{b}\)| ≠ 0.
But \(\vec{a}\) × \(\vec{b}\) = |\(\vec{a}\)| |\(\vec{b}\)| sin θ \(\hat {n} \) = 0
Thus, \(\vec{a}\) × \(\vec{b}\) = 0, even when |\(\vec{a}\)| ≠ 0, |\(\vec{b}\)| ≠ 0.
Question 9.
Find the area of the traiangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 3).
Solution:
The position vectors of vertices of ∆ ABC are (1, 1, 2), (2, 3, 5) and (1, 5, 5).
∴ \(\overrightarrow{\mathrm{AB}}\) = \(\overrightarrow{\mathrm{OB}}\) – \(\overrightarrow{\mathrm{OA}}\)
= (2\(\hat {i} \) + 3\(\hat {j} \) + 5\(\hat {k} \)) – (\(\hat {i} \) + \(\hat {j} \) + 2\(\hat {k} \))
= \(\hat {i} \) + 2\(\hat {j} \) + 3\(\hat {k} \).
\(\overrightarrow{\mathrm{AC}}\) = \(\overrightarrow{\mathrm{OC}}\) – \(\overrightarrow{\mathrm{OA}}\) = (\(\hat {i} \) + 5\(\hat {j} \) + 5\(\hat {k} \)) – (\(\hat {i} \) + \(\hat {j} \) + 2\(\hat {k} \))
= 0\(\hat {i} \) + 4\(\hat {j} \) + 3\(\hat {k} \) = 4\(\hat {j} \) + 3\(\hat {k} \).

![]()
Question 10.
Find the area of parallelogram whose adjacent sides are determined by the vectors \(\vec{a}\) = \(\hat {i} \) – \(\hat {j} \) + 3\(\hat {k} \)
and \(\vec{b}\) = 2\(\hat {i} \) – 7\(\hat {j} \) + \(\hat {k} \).
Solution:
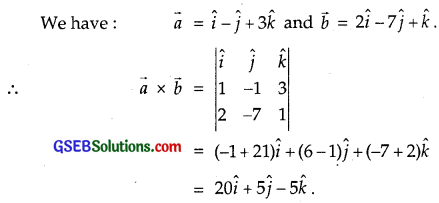
Area of the parallelogram whose sides are vectors \(\vec{a}\) and \(\vec{b}\)
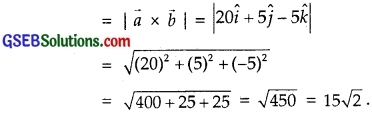
Question 11.
Let the vectors \(\vec{a}\) and \(\vec{b}\) are such that |\(\vec{a}\)| = 3 and |\(\vec{b}\)| = \(\frac{\sqrt{2}}{3}\), then \(\vec{a}\) × \(\vec{b}\) is a unit vector, if the angle between \(\vec{a}\) and \(\vec{b}\) is
(A) \(\frac{π}{6}\)
(B) \(\frac{π}{4}\)
(C) \(\frac{π}{3}\)
(D) \(\frac{π}{2}\)
Solution:

Also, |\(\vec{a}\) × \(\vec{b}\)| is a unit vector.
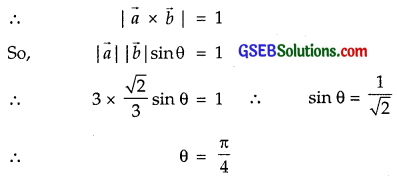
∴ Part (B) is the correct answer.
![]()
Question 12.
Area of rectangle having vertices A, B, C and D with position vectors
(- \(\hat {i} \) + \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \)), (\(\hat {i} \) + \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \)), (\(\hat {i} \) – \(\frac{1}{2}\) \(\hat {j} \) + 4\(\hat {k} \))
and (- \(\hat {i} \) – \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \)) is
Solution:
The position vectors of A and B are – \(\hat {i} \) + \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \)
and \(\hat {i} \) + \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \).
∴ \(\overrightarrow{\mathrm{AB}}\) = [1 – (- 1)]\(\hat {i} \) + 0.\(\hat {j} \) + 0.\(\hat {k} \)
∴ |\(\overrightarrow{\mathrm{AB}}\)| = 2
The postion vectors of A and D are – \(\hat {i} \) + \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \) and – \(\hat {i} \) – \(\frac{1}{2}\)\(\hat {j} \) + 4\(\hat {k} \).
∴ |\(\overrightarrow{\mathrm{AD}}\)| = (- \(\hat {i} \) + \(\hat {i} \)) + (- \(\frac{1}{2}\) – \(\frac{1}{2}\)) \(\hat {j} \) + 4\(\hat {k} \).
∴ |\(\overrightarrow{\mathrm{AD}}\)| = 1.
Area of rectangle ABCD = |\(\overrightarrow{\mathrm{AB}}\)| |\(\overrightarrow{\mathrm{AD}}\)| = 2 × 1 = 2.
∴ Part (C) is the correct answer.