Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 13 Probability Ex 13.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 13 Probability Ex 13.1
Question 1.
Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E ∩ F) = 0.2, find P(E/F) and P(F/E).
Solution:
(i) P(E/F) = \(\frac{E∩F}{P(F)}\) = \(\frac{0.2}{0.3}\) = \(\frac{2}{3}\).
(ii) P(F/E) = \(\frac{P(E∩F)}{P(E)}\) = \(\frac{0.2}{0.6}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\).
![]()
Question 2.
Compute P(A/B), if P(B) = 0.5 and P(A ∩ B) = 0.32.
Solution:
P(A/B) = \(\frac{P(A∩B)}{P(B)}\) = \(\frac{0.32}{0.5}\) = \(\frac{32}{50}\) = \(\frac{16}{25}\).
Question 3.
If P(A) = 0.8, P(B) = 0.5 and P(B/A) = 0.4, find
(i) P(A ∩ B)
(ii) P(A/B)
(iii) P(A ∪ B)
Solution:
(i) P(B/A) = \(\frac{P(A∩B)}{P(B)}\) ⇒ 0.4 = \(\frac{P(A∩B)}{0.8}\)
∴ P(A ∩ B) = 0.4 × 0.8 = 0.32.
(ii) P(A/B) = \(\frac{P(A∩B)}{P(B)}\) = \(\frac{0.32}{0.5}\) = \(\frac{32}{50}\) = \(\frac{16}{25}\).
(iii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.8 + 0.5 – 0.32 = 1.30 – 0.32
= 0.98.
Question 4.
Evaluate P(A ∪ B), if 2P(A) = P(B) = \(\frac{5}{13}\) and P(A/B) = \(\frac{2}{5}\).
Solution:
We have:
2P(A) = P(B) = \(\frac{5}{13}\)
⇒ P(A) = \(\frac{5}{26}\), P(B) = \(\frac{5}{13}\).
So, P(A/B) = \(\frac{P(A∩B)}{P(B)}\)
or \(\frac{2}{5}\) = \(\frac{P(A \cap B)}{\frac{5}{13}}\)
⇒ P(A ∩ B) = \(\frac{2}{5}\) × \(\frac{5}{13}\) = \(\frac{2}{13}\).
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{5}{26}\) + \(\frac{5}{13}\) – \(\frac{2}{13}\) = \(\frac{5+10-4}{26}\) = \(\frac{11}{26}\).
![]()
Question 5.
If P(A) = \(\frac{6}{11}\), P(B) = \(\frac{5}{11}\) and P(A ∪B) = \(\frac{7}{11}\), find
(i) P(A ∩ B)
(ii) P(A/B)
(iii) P(B/A)
Solution:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i) P(A ∩ B) = P(A) + P(B) – P(A ∪ B)
= \(\frac{6}{11}\) + \(\frac{5}{11}\) – \(\frac{7}{11}\) = \(\frac{4}{11}\).
(ii)
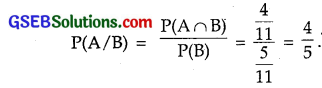
(iii)
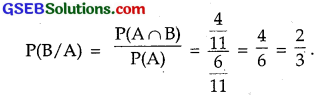
Determine P(E/F) in the questions 6 to 9:
Question 6.
A coin is tossed three times, where
(i) E : head on third toss , F : Heads on first two tosses
(ii) E : at least two heads, F : at most two heads
(iii) E : at most two tails F : at least one tail.
Solution:
(i) E = Head occurs on third toss as
{HHH, HTH, THH, TTH}
F : Heads on first two tosses = {HHH, HHT}
∴ E ∩ F = {HHH}

(ii) E : At least two heads = {HHT, HTH, THH, HHH}
F : At most two heads = {TTT, HTT, THT, HTT, HHT, HTH, THH}
∴ E ∩ F : {HHT, HTH, THH}
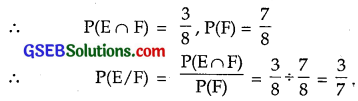
(iii) E : At most two tails = {HHT, THT, TTH, HHT, HTH, THH, HHH}
F : At least one tail = {THH, HTH, HHT, TTH, THT, HTT, TTT}
∴ E ∩ F : {HTT, THT, TTH, THH, HTH, HHT}
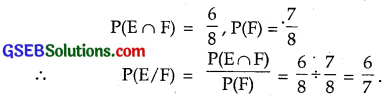
![]()
Question 7.
Two coins are tossed once, where
(i) E : tail appear on one coin ,F : one coin shows head
(ii) E : no tail appears, F : no head appears.
Solution:
(i) E : Tail appears on one coin = {TH, HT}
F : One coin shows head = {HT, TH}
∴ E ∩ F : {TH, HT}

(ii) E : no tail appears = {HH}
F : no head appears = {TT}
So, E ∩ F = ∅
∴ P(E/F) = \(\frac{P(E∩F)}{P(F)}\) = 0.
Question 8.
A dice is thrown three times, where
E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses.
Solution:
A dice is thrown three times.
E : 4 appears on third less
= {(1, 1, 4), (1, 2, 4), (1, 3, 4) (1, 6, 4)
(2, 1, 4, (2, 2, 4), (2, 3, 4) ……………… (2, 6, 4)
(3, 1, 4), (3, 2, 4), (3, 3, 4) …………………. (3, 6, 4)
(4, 1, 4), (4, 2, 4), (4, 3, 4) ………………….. (4, 6, 4)
(5, 1, 4), (5, 2, 4), (5, 3, 4) …………………. (5, 6, 4)
(6, 1, 4), (6, 2, 4), (6, 3, 4) …………………… (6, 6, 4)}
These are 36 cases.
F : 6 and 5 appears respectively on first two tosses
= {(6, 5, 1, (6, 5, 2), (6, 5, 3), (6, 5, 4), (6, 5, 5), (6, 5, 6)}
These are six cases.
Here, E ∩ F = {6, 5, 4}

![]()
Question 9.
Mother, father and son line up at random for a family picture, such that:
E : Son on one end
F : Father in middle
Solution:
Mother (m), Father (f) and Son (s) line up at random.
E : Son on one end : {(s, m, f), (s, f, m), (f, m, s), (m, f, s)}
F : Father in middle : {(m, f, s), (s, f, m)}

Question 10.
A black and red dice are rolled:
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black dice resulted in a 5.
(b) Find the conditional probability of obtaining the sum of 8, given that the red dice resulted in a number less than 4.
Solution:
(a) When two dice are thrown, a sum greater than 9 may be obtained as
A : {4, 6), (5, 5), (6, 4), (5, 6), (6, 5), (6, 6)}
B : Black dice will result in 5.
⇒ 5 is on black dice, any other number on red dice, i.e.,
= {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
So, A ∩ B = {(5, 5), (5, 6)}
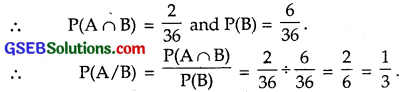
(b) A : Sum 8 is obtained = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}
B : red dice results in a number less than 4.
Either first or second dice is red
B = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)}
So, A ∩ B = {(2, 6), (3, 5)}

![]()
Question 11.
A fair dice is rolled. Consider the event E = {1, 3, 5} F = {2, 3} and G = {2, 3, 4, 5}. Find
(i) P(E/F) and P(F/E)
(ii) P(E/G), P(G/E)
(iii) P(E ∪ F/G) and P(E ∩ F/G)
Solution:
(i) E = {1, 3, 5}, F = {2, 3}, E ∩ F = {3}.

(ii) E = {1, 3, 5}, G = {2, 3, 4, 5}, E ∩ G = {3, 5}.

(iii) E = {1, 3, 5}, F = {2, 3}, G = {2, 3, 4, 5}
E ∩ G = {3, 5}, F ∩ G = {2, 3}, (E ∩ F) ∩ G = {3}
∴ P(E ∩ G) = \(\frac{2}{6}\), P(F ∩ G) = \(\frac{2}{6}\), P[(E ∩ F) ∩ G] = \(\frac{1}{6}\)
Now, P(E ∪ F/G) = P(E/G) + P(F/G) – P[(E ∩ F)/G]
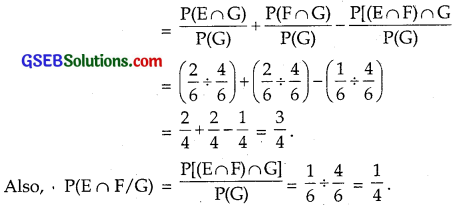
Question 12.
Assume that each child bom is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls, given that
(i) the youngest is a girl?
(ii) at least one is a girl?
Solution:
First and second girls are denoted by G1, G2 and boys by B1, B2
Sample space S = {(G1G2), (G1B2), (B1G2), (B1B2)}
Let A = Both the children are girls = {G1G2}
B = Youngest child is a girl = {G1G2, B1G2}
C = At least one is a girl = {G1B2, G1G2, B1G2}
So, A ∩ B = {G1G2}, A ∩ C = {G1G2}
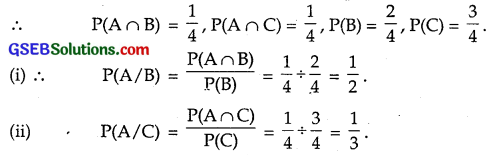
![]()
Question 13.
An instructor has a test bank consisting of 300 easy True/False questions, 200 difficult True/False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions.
If a question is selected at random from the test bank, what is the probability that it will be an easy questions given that it is a multiple choice questions?
Solution:
The given data may be tabulated as follows:

Let us denote E = Easy questions, D = Difficult questions, T = True/False questions and M = Multiple choice questions.
Number of easy multiple choice questions = 500.
Total number of questions = 1400.
P(E ∩ M) = Probability of selecting an easy and multiple choice question
= \(\frac{500}{1400}\).
Total number of multiple choice questions
= 500 + 400 = 900
P(M) = Probability of selecting one multiple choice question
= \(\frac{900}{1400}\)
∴ P(E/M) = \(\frac{P(E∩M)}{P(M)}\) = \(\frac{500}{1400}\) ÷ \(\frac{900}{1400}\) = \(\frac{5}{9}\).
Question 14.
Given that two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of the numbers on the dice is 4’.
Solution:
When the numbers appearing on throwing two dice are different.
⇒ The numbers are not the same
Total number of exhaustive cases = 36
Number of cases when doublets do not occur = 36 – 6 = 30
Cases when the sum is 4 are {(1, 3), (2, 2), (3, 1)}
Let A denotes the event when the sum of numbers on two dice is 4 and B is the event when the numbers appearing on the dice are different.
∴ A ∩ B = {(1, 3), (3, 1)}
So, P(A ∩ B) = \(\frac{2}{36}\), P(B) = \(\frac{30}{36}\).
∴ P(A/B) = \(\frac{P(A∩B)}{P(B)}\) = \(\frac{2}{36}\) ÷ \(\frac{3}{36}\) = \(\frac{1}{15}\).
![]()
Question 15.
Consider the experiment of throwing a dice, ‘if a multiple of 3 comes up, throw the dice again and if any other number comes toss a coin’.
Find the conditional probability of the event ‘the coin shows tail’, given that at least one dice shows a 3.
Solution:
Let there be n throws in which a multiple of 3 occurs every time.
Probability of getting a multiple of 3 (i.e., 3 or 6) in one throw
= \(\frac{2}{6}\) = \(\frac{1}{3}\).
∴ Probability of getting a multiple of 3 in n throws = (\(\frac{1}{3}\))n
Probability of getting a 6 in one throw = \(\frac{1}{6}\)
∴ Probability of getting a 6 in n throws = (\(\frac{1}{6}\))n.
⇒ Probability of getting at least a 3 in n throws = (\(\frac{1}{3}\))n – (\(\frac{1}{6}\))n
Let a multiple of 3 does not occur in (n + 1)th throw.
∴ Probability of getting 1, 2, 4, 5 (not a multiple of 3) in
(n + 1)th throw = \(\frac{4}{6}\) = \(\frac{2}{3}\).
In the next throw, a coin is tossed and tail occurs.
∴ Probability of getting a tail = \(\frac{1}{2}\)
⇒ Probability of getting at least a 3 and a tail in the end in

Question 16.
If P(A) = \(\frac{1}{2}\), P(B) = 0, then P(A/B) is
(A) 0
(B) \(\frac{1}{2}\)
(C) not defined
(D) 1
Solution:
P(A) = \(\frac{1}{2}\), P(B) = 0
P(A/B) = \(\frac{P(A∩B)}{P(B)}\) = \(\frac{P(A∩B)}{0}\) = Not defined.
∴ Part (C) is the correct answer.
![]()
Question 17.
If A and B are events such that P(A/B) = P(B/A), then
(A) A ⊂ B
(B) B = A
(C) A ∩ B = ∅
(D) P(A) = P(B)
Solution:
P(A/B) = P(B/A)
⇒ \(\frac{P(A∩B)}{P(B)}\) = \(\frac{P(A∩B)}{P(A)}\)
⇒ P(A) = P(B)
∴ Part (D) is the correct answer.