GSEB Solutions Class 12 Maths Chapter 4 Determinants Ex 4.4

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 4 Determinants Ex 4.4

Write minors and cofactors of elements of the following determinants:

Question 1.
(i) \(\left|\begin{array}{cc} 2 & -4 \\ 0 & 3 \end{array}\right|\)
(ii) \(\left|\begin{array}{cc} a & c \\ b & d \end{array}\right|\)
Solution:
(i) ∆ = \(\left|\begin{array}{cc} 2 & -4 \\ 0 & 3 \end{array}\right|\)
Minor of a₁₁ is M₁₁ = 3,
Minor of a₁₂ is M₁₂ = 0,
Minor of a₂₁ is M₂₁ = – 4,
Minor of a₂₂ is M₂₂ = 2.
Cofactor of a₁₁ = A₁₁ = (-1)¹⁺¹ M₁₁ = (-1)² x 3 = 3,
Cofactor of a₁₂ = A₂₁ = (-1)²⁺¹M₁₂ = 0,
Cofactor of a₂₁ = A₂₁ = (-1)²⁺¹ M₂₁ = – (- 4) = 4,
Cofactor of a₂₂ = A₂₂ = (-1)²⁺² M₂₂ = 2.

(ii)

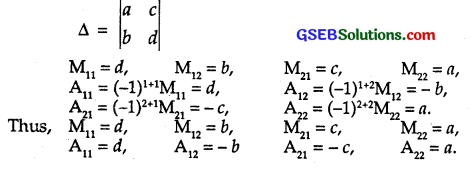
Question 2.
(i) \(\left|\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
(ii) \(\left|\begin{array}{ccc}
1 & 0 & 4 \\
3 & 5 & -1 \\
\theta & 1 & 2
\end{array}\right|\)
Solution:

Question 3.
Using cofactors of elements of second row, evaluate
∆ = \(\left|\begin{array}{rrr}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & -3
\end{array}\right|\).
Solution:

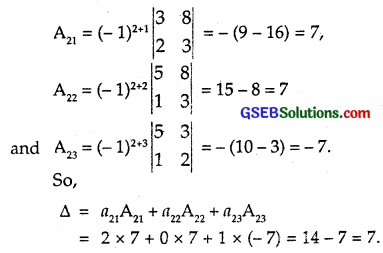
Question 4.
Using cofactors of elements of third column, evaluate
∆ = \(\left|\begin{array}{rrr} 1 & x & yz \\ 1 & y & zx \\ 1 & z & xy \end{array}\right|\).
Solution:
Elements of third column are yz, zx and xy.
A₁₃ = (-1)¹⁺³\(\left|\begin{array}{ll} 1 & y \\ 1 & z \end{array}\right|\) = z – y
A₂₃ = (-1)²⁺³\(\left|\begin{array}{ll} 1 & x \\ 1 & z \end{array}\right|\) = – (z – x) = – z + x
A₃₃ = (-1)³⁺³\(\left|\begin{array}{ll} 1 & x \\ 1 & y \end{array}\right|\) = (y – x)
∴ ∆ = a₁₃A₁₃ + a₂₃A₂₃ + a₃₃A₃₃
= yz(z – y) + zx(- z + x) + xy(y – x)
= yz² – y²z – xz² + x²z + xy² – x²y
= (- y²z + yz²) + (xy² – xz²) + (- x²y + x²z)
= – yz(y – z) + x(y² – z²) – x²(y – z)
= (y-z)[- yz + (y + z) – x²]
= (y-z)[-yz + xy+ xz-x²]
= (y – z)[xy – yz – x² + xy]
= (y – z)[z(x – y) – x(x – y)]
= (y – z)(x – y)(z – x)
= (x – y)(y – z)(z – x).

Question 5.
If A = \(\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|\) and A_ij is the cofactor of a_ij, then value of ∆ is given by
(A) a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
(B) a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
(C) a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
(D) a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁
Solution:
A = Sum of the products of elements of a row or column with the corresponding cofactors.
Here, Part (D) is the required answer, because elements of 1 column are multiplied by their corresponding cofactors.
So, a₁₁A₁₁ + a₂₁A₂₁ + a₃₁A₃₁.