GSEB Solutions Class 12 Maths Chapter 8 Application of Integrals Ex 8.2

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Ex 8.2 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Ex 8.2

Question 1.
Find the area of the circle 4x² + 4y² = 9 which is interior to the parabola x² = 4y.
Solution:
Area is bounded by the circle 4x² + 4y² = 9 and interior of the parabola x² = 4y.
Putting x² = 4 in x² + y² = \(\frac{9}{4}\),

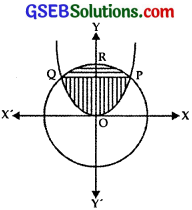
we get 4y + y² = \(\frac{9}{4}\).
or y² + 16y – 9 = 0
⇒ (2y + 9)(2y – 1) = 0
y = \(\frac{1}{2}\), – \(\frac{9}{2}\); y ≠ – \(\frac{9}{2}\) as y is positive.
∴ y = \(\frac{1}{2}\).
Radius of the circle = \(\frac{3}{2}\)
Area of the region required = Area of the region OPRQ
= (area of the region OPQ) + (area of the region PQR)
= 2 × area of the region OPT + 2 × area of the region TPQ

Question 2.
Find the area bounded by the curve (x – 1)² + y² = 1 and x² + y² = 1.
Solution:
Given circles are
x² + y² = 1 ………….. (1)
and (x – 1)² + y² = 1 ……………….. (2)
Centre of (1) is O (0, 0) and radius = 1.
Both these circles are symmetrical about x-axis.

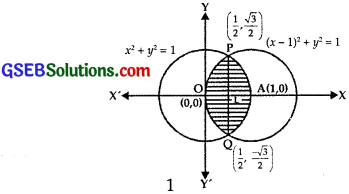
Solving (1) and (2) we get,
– 2x + 1 = 0 ⇒ x = \(\frac{1}{2}\).
Then, y² = 1 – (\(\frac{1}{2}\))² = \(\frac{3}{4}\) ⇒ y = ±\(\frac{\sqrt{3}}{2}\).
∴ The points of intersection are P(\(\frac{1}{2}\), \(\frac{\sqrt{3}}{2}\)) and Q(\(\frac{1}{2}\), – \(\frac{\sqrt{3}}{2}\)).
It is clear from the figure that the shaded portion is the region whose area is required.
Required area = area OQAPO
= 2 × area of the region CLAP
= 2 × (area of the region OLPO + area of the region LAPL)

Question 3.
Find the area of the region bounded by the curve y = x² + 2 and the line y = x, x = 0 and x = 3.
Solution:
Equation of the parabola is
y = x² + 2
or x² = (y – 2)
Its vertex is (0, 2). Axis is y-axis.
Boundary lines are
y = x, x = 0 and x = 3.
Graphs of the curve and lines have been shown in the figure.

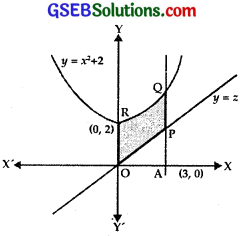
Area of the region PQRO
= Area of the region OAQR – Area of region OAP

Question 4.
Using integration, find the area of the region bounded by a traingle whose vertices are (- 1, 0), (1, 3) and (3, 2).
Solution:
The points A(- 1, 0), B(1, 3) and C(3, 2) are plotted and joined.

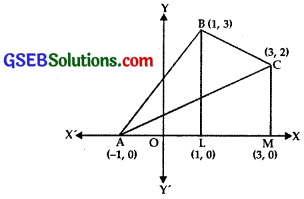
Area of ∆ ABC = Area of ∆ ABL + Area of trapezium BLMC – Area of ∆ ACM
The equation of the line joining the points (x₁, y₁) and (x₂, y₂) is

Area of trapezium BCML.
= Area bounded by BC, x-axis x = 1, x = 3.

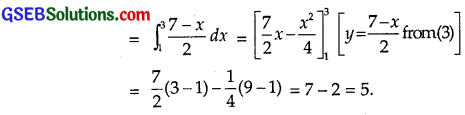
Area of ∆ ACM.
(Area bounded by AC, y = \(\frac{x+1}{2}\) x-axis and x = 3)

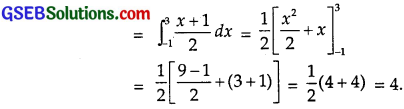
From (1),
∴ Area of ∆ ABC = 3 + 5 – 4 = 4 sq.units.

Question 5.
Using integration, find the area of the triangular region, whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
Solution:
The given lines are
y = 2x + 1 ………… (1)
y = 3x + 1 …………. (2)
x = 4 ………….. (3)
Subtracting (1) from eq. (2), we get 0 = x,
i.e., x = 0.
Putting x = 0 in eq. (1), we get y = 1.
∴ Lines (2) and (1) intersect at A (0, 1).
Putting x = 4 in eq. (2), we get
y = 12 + 1 = 13.
∴ The lines (2) and (3) intersect at B(4, 13).
Putting x = 4 in eq. (1), we get
y = 8 + 1 = 9.
∴ Lines (1) and (2) intersect at C(4, 9).
Area of ABC
= Area of trapezium OLBA – Area of trapezium OLCA ………… (4)

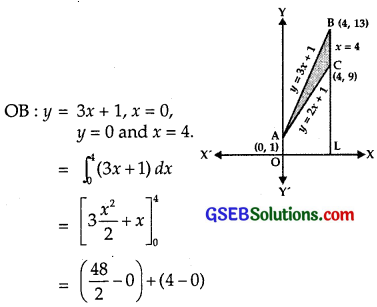
Area of trapezium OLCA
= Area of region bounded of
OC : y = 2x + 1, x = 0 and x = 4 and y = 0

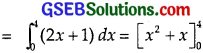
= (16 – 0) + (4 – 0) = 20.
Putting these values in (4),
area of ∆ ABC = 28 – 20 = 8 sq.units.

Choose the correct answers in the following questions 7 and 8:

Question 6.
Smaller area bounded by the circle x² + y² = 4 and the line x + y = 2
(A) 2(π – 2)
(B) π – 2
(C) 2π – 1
(D) 2(π + 2)
Solution:
A circle of radius 2 and centre at O is drawn. The line AB : x + y = 2 we passes through (2, 0) and (0, 2).

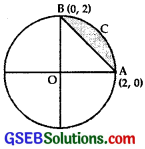
Area of the region ACB
= Area of quadrant OAB – Area of ∆ OAB …………. (1)
Now, x² + y² = 4
∴ y² = 4 – x² or y = \(\sqrt{4-x^{2}}\)
∴ Area of quadrant OAB

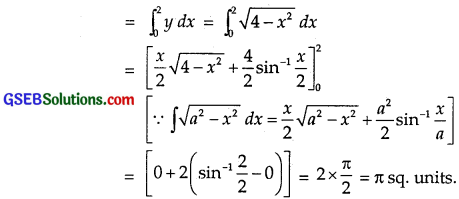
Area of ∆ ABC = Area of the region bounded by
AB : x + y = 2 or y = 2 – x
and x = 0, y = 0

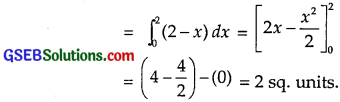
Putting these values in (1), we get area of region ACB = π – 2
∴ Part (B) is the correct answer.

Question 7.
Area lying between the curves y² = 4x and y = 2x is
(A) \(\frac{2}{3}\)
(B) \(\frac{1}{3}\)
(C) \(\frac{1}{4}\)
(D) \(\frac{3}{4}\)
Solution:
The curve is y² = 4x …………… (1)
and the line is y = 2x …………….. (2)
From (1) and (2),
(4x)² = 4
∴ x(x – 1) = 0
x = 0, x = 1.

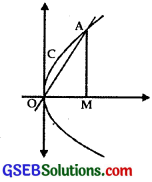
Curves (1) and (2) intersect at O(0, 0) and A(1, 2).
∴ Area of region OACO
= Area of region OMACO – Area of OMA ………………. (3)
Now, area of region OMACO
= Area of region bounded by curve OCA
y = \(\sqrt{4x}\), x-axis and x = 1.

Area of ∆ OMA = Area of region bounded by
OA : y = 2x, x = 1 and x-axis

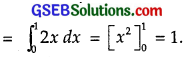
Putting these values in (3), we get
are of region OMACO
= \(\frac{4}{3}\) – 1 = \(\frac{1}{3}\) sq.units.
∴ Part(B) the correct answer.