GSEB Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.4

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 6 Application of Derivatives Ex 6.4

Question 1.
Using differentials, find the approximate value of each of the following upto 3 places of decimal :
(i) \(\sqrt{25.3}\)
Solution:

(ii) \(\sqrt{49.5}\)
Solution:

(iii) \(\sqrt{0.6}\)
Solution:

(iv) (0.009)^{\(\frac { 1 }{ 3 }\)}
Solution:
Let y = x^{\(\frac { 1 }{ 3 }\)}
Also, let x = 0.008, ∆x = 0.001,
so, that x + ∆x = 0.009.

∴ Approximate value of ∆y = dy = 0.008.
Hence, from (1), we have :
(0.009)^{\(\frac { 1 }{ 3 }\)} – o.2 + 0.008 = 0.208 (approx.)

(v) (0.999)^{\(\frac { 1 }{ 10 }\)}
Solution:

(vi) (15)^{\(\frac { 1 }{ 4 }\)}
Solution:
Let y = ^{\(\frac { 1 }{ 4 }\)}.
Also, let x = 16, ∆x = – 1, so that
x + ∆x = 15.

∴ Approximate value of ∆y = dy = 0.03125.
Hence, from (1), we have :
(15)^{\(\frac { 1 }{ 4 }\)} = 2 – 0.03125 = 1.969 (approx)

(vii) (26)^{\(\frac { 1 }{ 3 }\)}
Solution:
Let y = x^{\(\frac { 1 }{ 3 }\)}.
Also, let x = 27, ∆x = – 1, so that
x + ∆x = 26
Now, ∆y = (x + ∆x)³-x³
= (26)^{\(\frac { 1 }{ 3 }\)} – (27)^{\(\frac { 1 }{ 3 }\)} = (26)^{\(\frac { 1 }{ 3 }\)} – 3.
⇒ (26)^{\(\frac { 1 }{ 3 }\)} = 3 + ∆y

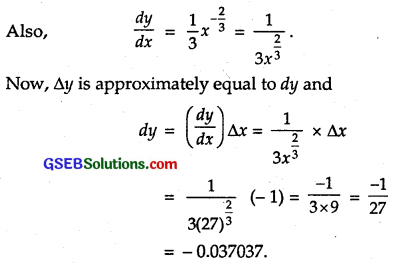
∴ Approximate value of ∆y = dy = – 0.037037.
Hence, from (1), we have :
(26)^{\(\frac { 1 }{ 3 }\)} = 3 – 0.37037
= 2.963 (approx.).

(viii) (255)^{\(\frac { 1 }{ 4 }\)}
Solution:
Let y = f(x) = x^{\(\frac { 1 }{ 4 }\)}
Let x = 256, x + ∆x =255, so that ∆x = 255 – 256 = – 1.

Approximate value of ∆y = dy = – 0.0039.
Hence, from (1), we have :
(255)^{\(\frac { 1 }{ 4 }\)}= 4 – 0.0039 = 3.9961.

(ix) (82)^{\(\frac { 1 }{ 4 }\)}
Solution:

(x) (401)^{\(\frac { 1 }{ 2 }\)}
Solution:

(xi) (0.0037)^{\(\frac { 1 }{ 2 }\)}
Solution:
Let y = \(\sqrt{x}\)
Also, let x = 0.0036 and ∆x = 0.0001, so that x + ∆x = 0.0037

Approximate value of ∆y = dy = 0.000833.
Hence, from (1), we have :
\(\sqrt{0.0037}\) = 0.06 + 0.00083
= 0.061 (approx.)

(xii) (26.57)^{\(\frac { 1 }{ 3 }\)}
Solution:

(xiii) (81.5)^{\(\frac { 1 }{ 4 }\)}
Solution:
Let y = x^{\(\frac { 1 }{ 4 }\)}, x = 81 and ∆x = 0.5

(xiv) (3.968)^{\(\frac { 3 }{ 2 }\)}
Solution:

(xv) (32.15)^{\(\frac { 1 }{ 5 }\)}
Solution:

Question 2.
Find the approximate value of f(2.01), where f(x) = 4x² + 5x +2.
Solution:
Let x + ∆x = 2.01, x = 2 and ∆x = 0.01.
So, f(x + ∆x) = f(2.01) and
f(x) = f(2) = 4 . 2² + 5.2 + 2
= 16 + 10 + 2 = 28
Now, f(x) = 8x + 5.
Also, f(x + ∆x) = f(x) + ∆f(x)
= f(x) + f'(x). ∆x
= 28 + (8x + 5) x ∆x
= 28 + (16 + 5) x 0.01
= 28 + 21 x 0.01 = 28 + 0.21 =28.21.
Hence, f(2.01) = 28.21.

Question 3.
Find the approximate value of f(5.001), where f(x) = x³ – 7x² +15.
Solution:
Let x + ∆x = 5.001, x = 5 and ∆x = 0.001.
So, f(x) = f(5) = 5³ – 7 x 5² + 15
= 125-175 +15 = -35.
Also, f(x + ∆x) = f(x) + ∆f(x) = f(x) + f(x). ∆x
= (x³ – 7x² + 15) + (3x² – 14x) x ∆x
∴ f(5.001) = – 35 + (3 x 5² – 14 x 5) x 0.001
= – 35+ (75 – 14 x 5) x 0.001
= – 35 + 5 x 0.001
= – 35 + 0.005
= – 34.995.

Question 4.
Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.
Solution:
The side of the cube = x metres.
∴ Increase in side = 1% = 0.01 × x = 0.01 x
Volume of cube V =x³
∴ Approximate change in volume = AV
= \(\frac { dv }{ dx }\) x ∆x
= 3x² x 0.01 x = 0.03 x³ m³.

Question 5.
Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%.
Solution:
The side of the cube = x metres.
∴ Decrease in side = 1% = 0.01x
So, Increase in side = ∆x = – 0.01 x.
Surface area of cube = 6x² m² = s (say)
Approximate change in surface area of cube = ∆s
= \(\frac { ds }{ dx }\) x ∆x
= 12x × (- 0.01 x) = – 0.12 x² m².

Question 6.
If the radius of a sphere measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.
Solution:
Radius of the sphere = 7 m.
Error in measurement of radius = ∆r = 0.02 m.
Volume of the sphere V = \(\frac { 4 }{ 3 }\)πr³
= 4 π r² x ∆r
= 4π x 7² x 0.02 = 3.92 π m³.

Question 7.
If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.
Solution:
Radius of the sphere = 9 m.
Error in measurement = ∆r = 0.03 m.
Surface area of sphere S = 4 π r²
∴ ∆S = \(\frac { dS }{ dr }\) x ∆r = 8π r x ∆r dr
= 8π x 9 x 0.03
= 2.16 π m².

Question 8.
If f(x) = 3x² + 15x + 5, then the approximate value of f(3.02) is
(A) 47.66
(B) 57.66
(C) 67.66
(D) 77.66
Solution:
x + ∆x = 3.02, where x = 3, ∆x = 0.02.
∆ f(x) = f(x + ∆x) – f(x)
⇒ f(x + ∆x) = f(x) + ∆ f(x)
= f(x) + f'(x) ∆x … (1)
Now, f(x) = 3x² + 15x + 5.
So, f(3) = 3 . 3² + 15.3 + 5 = 27 + 45 + 5 = 77
and f'(x) = 6x + 15.
⇒ f'(3) = 6 x 3 + 15 = 18 + 15 = 33.
Putting these values in (1), we get
∴ f(3.02) = 87 + 33 x 0.02 = 77 + 0.66 = 77.66.
∴ Part (D) is the correct answer.

Question 9.
The approximate change in volume of a cube of side x metres caused by increasing the side by 3% is
(A) 0.06 x³m³
(B) 0.6 x³m³
(C) 0.09 x³m³
(D) 0.9 x³m³
Solution:
Side of a cube = x metres.
Volume of cube = x³m³
Now, ∆x = 3% of x = 0.03 x.
Let ∆V be the change in volume.
So, ∆V = \(\frac { dv }{ dx }\) x ∆x = 3x² x ∆x
But ∆x = 0.03x.
∴ ∆V = 3x² x 0.03x = 0.09 x³m³.
∴ Part (C) is the correct answer.