Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Ex 8.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Ex 8.1
Question 1.
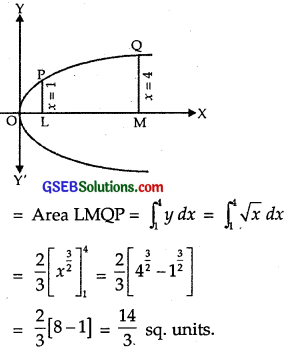
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Solution:
The curve y2 = x is a parabola with vertex at origin.
Axis of x is the line of symmetry, which is the axis of parabola.
The area of the region bounded by the curve, x = 1, x – 4 and the x-axis.
![]()
Question 2.
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Solution:
The given curve is y2 = 9x,
which is a parabola with vertex at (0, 0) and axis along x-axis.
It is symmetrical about x-axis as it contains only even powers of y,
x – 2 and x = 4 are straight lines parallel to y-axis at a positive distances of 2 and 4 units from it respectively.
∴ Required area = area ABCD

![]()
Question 3.
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
Solution:
The given curve x2 = 4y is a parabola with vertex at (0, 0).
Also, since it contains only even powers of x, it is symmetrical about y-axis.
y = 2 and y = 4 are straight lines parallel to x-axis at a positive distances of 2 and 4 from it respectively.
∴ Required area = area ABCD

![]()
Question 4.
Find the area of the region bounded by the ellipse \(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{9}\) = 1.
Solution:
The equation of the ellipse if \(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{9}\) = 1.
The given ellipse is symmetrical about both axes as it contains only even powers of y and x.
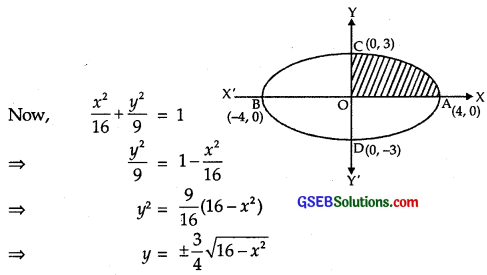
Now, area bounded by the ellipse
= 4 × (area of ellipse in first quadrant)
= 4(area OAC) = 4\(\int_{0}^{4}\)y dx
= \(\int_{0}^{4}\)\(\frac{3}{4}\)\(\sqrt{16-x^{2}}\)dx
[∵ y ≥ 0 in first quadrant]
Put x = 4 sin θ so that dx = 4 cos θ dθ.
Now, when x = 0, θ = 0 and when x – 4, θ = \(\frac{π}{2}\).

![]()
Question 5.
Find the area of the region bounded of the ellipse \(\frac{x^{2}}{4}\) + \(\frac{y^{2}}{9}\) = 1.
Solution:

It is an ellipse centre (0, 0), the length of semi-major axis = 3 and that of semi-minor axis = 2.
Its rough sketch is shown in the figure.
∴ Area bounded of the ellipse
= 4 × area of the region AOB
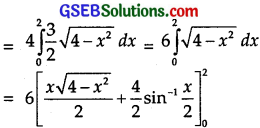
= 6[(0 + 2 sin-1) – (0 + sin-1(0))]
= 6[2.\(\frac{π}{2}\)] = 6π sq.units.
Question 6.
Find the area of the region in the first quadrant enclosed by the x-axis,
the line x = \(\sqrt{3}\)y and the circle x2 + y2 = 4.
Solution:
Consider the two equations
x2 + y2 = 4 ………………. (1)
and x = \(\sqrt{3}\)y, i.e; y = \(\frac{1}{\sqrt{3}}\)x ………………. (2)
(1) x2 + y2 = 4 is a circle with centre O (0, 0) and radius = 4.
(2) y = \(\frac{1}{\sqrt{3}}\)x is a straight line passing through (0, 0) and intersecting the circle at B(\(\sqrt{3}\), 1).
The required area = shaded region
= area OBL + area LBA

![]()
Question 7.
Find the area of the smaller part of the circle
x2 + y2 = a2 cut off by the line x = \(\frac{a}{\sqrt{2}}\).
Solution:
The equations of the given curves are
x2 + y2 = a2 …………………. (1)
and x = \(\frac{a}{\sqrt{2}}\) ………………. (2)
Clearly, (1) represents a circle and (2) is the equation of a straight line parallel to y-axis at a distance
\(\frac{a}{\sqrt{2}}\) units to the right of y-axis.
Solving (1) and (2), we get
\(\frac{a^{2}}{2}\) + y2 = a2 ⇒ y2 = \(\frac{a^{2}}{2}\)
⇒ y = \(\frac{a}{\sqrt{2}}\).
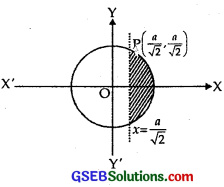
∴ P(\(\frac{a}{\sqrt{2}}\), \(\frac{a}{\sqrt{2}}\)) is the point of intersection of curves (1) and (2) in the first quadrant.
The smaller region bounded by these two curves is the shaded portion shown in the figure.
∴ Required area = shaded region
= 
Question 8.
The area between x = y2 and x = 4 is divided into two equal parts by the line x1 = a. Find the value of a.
Solution:
Graph of the curve x = y2 is a parabola as shown in the figure.
Its vertex is O and axis is x-axis.
QR is the ordinate along x = 4
∴ Area of the region
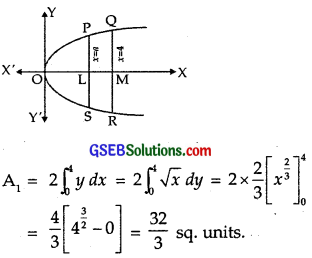
Area of the region bounded by the curve and ordinate x = a is
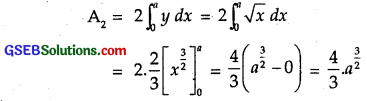
Now PS [x = a] divides the area of the region ORQ into two equal parts.
∴ Area of region ORQ = 2 Area of the region OSP
∴ A1 = 2A2
∴ \(\frac{32}{3}\) = 2.\(\frac{4}{3}\)a3/2
a3/2 = 4
∴ a = 42/3 units.
![]()
Question 9.
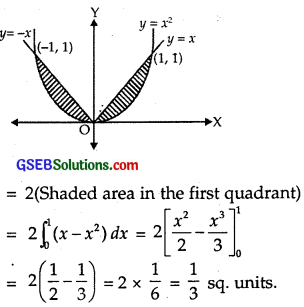
Find the area of the region bounded by the parabola y = x2 and lines y = |x|.
Solution:
Clearly, x2 = y represents a parabola with vertex at (0, 0),
positive direction of y-axis as its axis and it opens upwards.
y = |x|, i.e., y = x and y = – x represent two lines passing through the origin and making an angle of 45° and 135° with the positive direction of the x-axis.
The required region is the shaded region as shown in the figure. Since both the curves are symmetrical about y-axis. So,
Required area = 2(Shaded area in the first quadrant)
Question 10.
Find the area bounded by the curve x2 = 4y and the straight line x = 4y – 2.
Solution:
Given curve is x2 = 4y, ……………… (1)
which is an upward parabola with vertex at (0, 0) and is symmetrical about y-axis.
Equation of the line is x = 4y – 2 …………….. (2)
Solving (1) and (2) simultaneously, we get
(4y – 2)2 = 4y
⇒ 16y2 – 16y + 4 = 4y
⇒ 16y2 – 20y + 4 = 0
⇒ 4y2 – 5y + 1 = 0
⇒ (4y – 1)(y – 1) = 0
⇒ y = \(\frac{1}{4}\), 1
From (2), when y = \(\frac{1}{4}\), x = 1 – 2 = – 1.
When y = 1, x = 4 – 2 = 2.
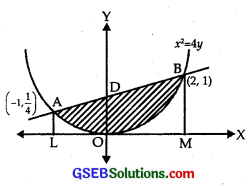
∴ A(- 1, \(\frac{1}{4}\)) and (2, 1) are the points of intersection of (1) and (2).
Clearly, from the figure the shaded portion OBDAO is the region of the required area.
Required area = area LOMBDA – area LMBOAL ……………. (3)
Now, area LMBDA = \(\int_{-1}^{2}\) ydx
(where x = 4y – 2 ⇒ y = \(\frac{1}{4}\)(x + 2))

From (3), (4) and (5), the required area
= \(\frac{15}{8}\) – \(\frac{3}{4}\) = \(\frac{9}{8}\) sq.units.
![]()
Question 11.
Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
Solution:
The curve y2 = 4x is a parabola as shown in the figure.
Axis of the parabola is .r-axis.
The area of the region bounded by the curve y2 = 4x and the line x = 3 is A.
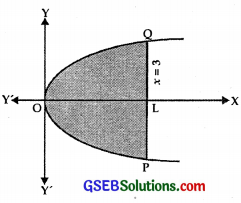
= Area of region PQO
= 2 area of the region OLQ
[Note : Areas below and above x-axis are equal.]

Choose the correct answers in the following questions 12 and 13:
Question 12.
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
(A) π
(B) \(\frac{π}{2}\)
(C) \(\frac{π}{3}\)
(D) \(\frac{π}{4}\)
Solution:
A circle of radius 2 is drawn.
The line OP is x = 0 and AQ is x = 2.
∴ Area A of the required region OAP
= \(\int_{0}^{2}\) y dx …………… (1)
Equation of the circle is x2 + y2 = 4

∴ Part (A) is the correct answer.
![]()
Question 13.
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is
(A) π
(B) \(\frac{9}{4}\)
(C) \(\frac{9}{3}\)
(D) \(\frac{9}{2}\)
Solution:
The curve y2 = 4x is the parabola and MP is the line y = 3.
The area of the region bounded by y2 = 4x, y-axis and y = 3 is
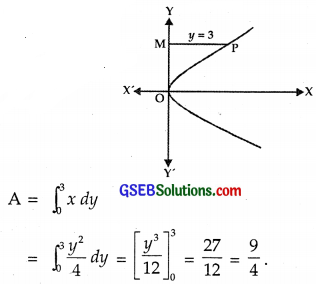
∴ Part (B) is the correct answer.