Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.3
In each of the questions 1 to 5, form a differential equation representing the given family of curves by eliminating arbitrary constants a and b:
Question 1.
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
Solution:
\(\frac{x}{a}\) + \(\frac{y}{b}\) = 1
Differentiating w.r.t. x,
\(\frac{1}{a}\) + \(\frac{y’}{b}\) = 0.
Again differentiating,
\(\frac{1}{a}\).y” = 0 or y” = 0.
∴ Required differential equation is y” = 0
![]()
Question 2.
y2 = a(b2 – x2)
Solution:
y2 = a(b2 – x2) ………………….. (1)
Differentiating w.r.t. x,
2yy’ = a(0 – 2x) = – 2ax ………………… (2)
Again differentiating,
2(y2 + yy’) = – 2a ………………… (3)
Dividing (3) by (2) we get,
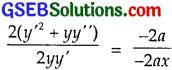
⇒ x(y2 + yy”) = yy’,
which is the required differential equation.
It can also be written as xy\(\frac{d^{2} y}{d x^{2}}\) + x(\(\frac{dy}{dx}\))2 – y\(\frac{dy}{dx}\) = 0.
Question 3.
y = a e3x + b e-2x
Solution:
y = a e3x + b e-2x ……………………. (1)
Differentiating w.r.t. x,
y’ = 3ae3x – 2be-2xx ……………….. (2)
Again differentiating,
y” = 9a3x + 4be-2x ………………….. (3)
Multiplying equation (1) by 2 and add with (2) to obtain:
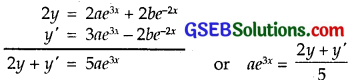
Multiplying (1) by 3 and subtract (2) from it to obtain:
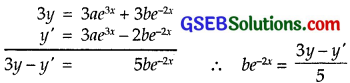
Putting values of ae3x and be-2x in (3), we get
y” = 9(\(\frac{2y+y’}{5}\)) + 4(\(\frac{3y-y’}{5}\))
or 5y” = 9(2y + y’) + 4(3y – y’)
= 30y + 5y’
or y” – y’ – 6y = 0
∴ Required differential equation is
\(\frac{d^{2} y}{d x^{2}}\) – \(\frac{dy}{dx}\) – 6y = 0.
![]()
Question 4.
y = e2x(a + bx)
Solution:
The curve is y = e2x(a + bx) ………………. (1)
∴ y’ = 2e2x(a + bx) + e2x.
= e2x(2a + b + 2bx) ……………….. (2)
Multiply eq. (1) and (2) and subtract it from (2) to get:
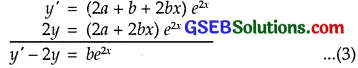
Differentiating eq. (3),
y” – 2y’ = 2be2x …………….. (4)
Dividing (4) by (3), we get
or y” – 2y’ = 2(y’ – 2y)
or y” = 4y’ + 4y = 0
∴ The required differential equation is
\(\frac{d^{2} y}{d x^{2}}\) – 4\(\frac{dy}{dx}\) + 4y = 0.
Question 5.
y = ex(a cos x + b sin x)
Solution:
The curve is y = ex(a cos x + b sin x) ……………. (1)
Differentiating w.r.t. x, we get
y’ = ex(a cos x + b sin x) + ex(- a sin x + b cos x)
= ex[(a + b)cos x – (a – b)sin x] ……………. (2)
Again differentiating, we get
y” = ex(acos x + bsin x) + ex(- asin x + bcos x)
= ex[(a + b)cos x – (a – b)cos x]
= ex[2b cos x – 2a sin x]
= 2ex(b cos x – a sin x)
or \(\frac{y”}{2}\) = ex(b cos x – a sin x) ……………….. (3)
Adding (1) and (3),
y + \(\frac{y”}{2}\) = ex[(a + b)cos x – (a – b)sin x] = y’
or 2y + y” = 2y’
⇒ y” – 2y’ + 2y = 0.
Hence, the required differential equation is
\(\frac{d^{2} y}{d x^{2}}\) – 2\(\frac{dy}{dx}\) + 2y = 0.
![]()
Question 6.
From the differential equation of the family of circles touching the y-axis at origin.
Solution:
The equation of the circle with centre (a, 0) and radius a, which touches y-axis at origin, is
(x – a)2 + y2 = a2
or x2 + y2 = 2ax ……………. (1)
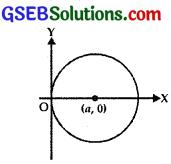
Differentiating w.r.t. x,
2x + 2y y’ = 2a
or x + yy’ = a
Putting value of a in (1), we get
x2 + y2 = 2x(x + yy’)
= 2x2 + 2xy y’.
∴ Required differential equation is
2xy\(\frac{dy}{dx}\) + x2 – y2 = 0.
Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solution:
Equation of parabola having vertex at the origin and axis along positive y-axis is
x2 = 4ay ………….. (1)
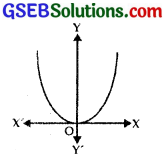
where a is the parameter.
Differentiating w.r.t. x,
2x = 4ay’ ………………. (2)
Dividing (2) by (1) we get,
\(\frac{2 x}{x^{2}}\) = \(\frac{2ay’}{4ay}\) ⇒ \(\frac{y’}{y}\) = \(\frac{2}{x}\)
∴ xy’ = 2y.
∴ Required differential equation is
x\(\frac{dy}{dx}\) – 2y = 0.
![]()
Question 8.
Form the differential equation of family of ellipses having foci on y-axis.
Solution:
The equation of family of ellipses having foci on y-axis is
\(\frac{x^{2}}{b^{2}}\) + \(\frac{y^{2}}{a^{2}}\) = 1, a > b …………. (1)
Differentiating w.r.t. x,

Again differentiating,

Putting this value of \(\frac{1}{b^{2}}\) in (2), we get
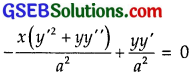
or x(y’2 + yy”) = yy’
or xyy” + xy’2 – yy’ = 0.
∴ Required differential equation is
xy \(\frac{d^{2} y}{d x^{2}}\) + x(\(\frac{dy}{dx}\))2 – y(\(\frac{dy}{dx}\)) = 0.
Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and the centre at origin.
Solution:
Equation on family of hyperbolas with centre at the origin and foci on x-axis is
\(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 ………………. (1)
Differentiating w.r.t. x,

Again differentiating,

Question 10.
Form the differential equation of family of circles having centres on y-axis and radius 3 units.
Solution:
Let the centre be [0, b].
∴ Equation of family of circles of radius 3 is
x2 + (y – b)2 = 9 ………….. (1) [∵ r = 3]
Differentiating w.r.t. x,
2x + 2(y – b)y’ = 0 or y – b = – \(\frac{x}{y’}\)
Putting this value of (y – b) in (1), we get
x2 + (- \(\frac{x}{y’}\))2 = 9
or x2y’2 + x2 = 9y’2 or (x2 – 9)y’2 + x2 = 0
∴ Required differential equation is (x2 – 9) (\(\frac{dy}{dx}\))2 + x2 = 0.
![]()
Choose the correct answers in the following questions 11 and 12:
Question 11.
Which of the following equations has y = c1ex + c2e-x as the general solution?
(A) \(\frac{d^{2} y}{d x^{2}}\) + y = 0
(B) \(\frac{d^{2} y}{d x^{2}}\) – y = 0
(C) \(\frac{d^{2} y}{d x^{2}}\) + 1 = 0
(D) \(\frac{d^{2} y}{d x^{2}}\) – 1 = 0
Solution:
Family of curve is y = c1ex + c2e-x …………….. (1)
Differentiating w.r.t. x,
y’ = c1ex – c2e-x
y” = c1ex + c2e-x = y
∴ y” – y = 0
Solution is \(\frac{d^{2} y}{d x^{2}}\) – y = 0.
∴ Part (B) is the correct answer.
![]()
Question 12.
Which of the following differential equations has y = x as one of its particular solution?
(A) \(\frac{d^{2} y}{d x^{2}}\) – x2\(\frac{dy}{dx}\) + xy = 0
(B) \(\frac{d^{2} y}{d x^{2}}\) + x\(\frac{dy}{dx}\) + xy = x
(C) \(\frac{d^{2} y}{d x^{2}}\) – x2\(\frac{dy}{dx}\) + xy = 0
(D) \(\frac{d^{2} y}{d x^{2}}\) + x \(\frac{dy}{dx}\) + xy = 0
Solution:
The curve is y = x.
Differentiating w.r.t. x,
y’ = 1 and y” = 0.
Now consider part (C).
\(\frac{d^{2} y}{d x^{2}}\) – x2\(\frac{dy}{dx}\) + xy = 0 – x2.1 + x . x
∵ y = x
= – x2 + x2 = 0.
Hence, Part (C) is the correct answer.