GSEB Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.4

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.4 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 9 Differential Equations Ex 9.4

For each of the differential equations in questions 1 to 10, find the general solution:
Question 1.
\(\frac{dy}{dx}\) = \(\frac{1-cosx}{1+cosx}\)
Solution:

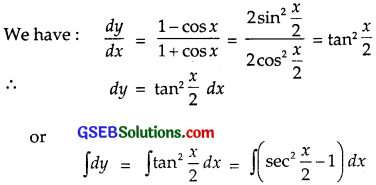
∴ y = 2 tan \(\frac{x}{2}\) – x + C
This is the required solution.

Question 2.
\(\frac{dy}{dx}\) = \(\sqrt{4-y^{2}}\) (- 2 < y < 2)
Solution:
\(\frac{dy}{dx}\) = \(\sqrt{4-y^{2}}\) or \(\frac{d y}{\sqrt{4-y^{2}}}\) = dx
Integrating both sides, we get
∫ \(\frac{d y}{\sqrt{4-y^{2}}}\) = ∫dx
⇒ sin^-1\(\frac{y}{2}\) = x + C or y = 2 sin(x + C).
which is the required solution.

Question 3.
\(\frac{dy}{dx}\) + y = 1 (y ≠ 1)
Solution:
Given differential equation is \(\frac{dy}{dx}\) + y = 1
or \(\frac{dy}{dx}\) = 1 – y or \(\frac{dy}{1-y}\) = dx
Integrating both sides, we get
∫ – log (1 – y) = x + log C
∴ x = – log C – log (1 – y) = – log C(1 – y)
∴ C(1 – y) = e^-x
or C(1 – y)e^x = 1
⇒ 1 – y = \(\frac{1}{C}\)e^-x ⇒ y = 1 – \(\frac{1}{C}\)e^-x.
Put – \(\frac{1}{C}\) = A; y = 1 + Ae^-x is the required solution.

Question 4.
sec²x tan y dx + sec²y tan x dy = 0
Solution:
We have:
sec²x tan y dx + sec²y tan x dy = 0
⇒ \(\frac{\sec ^{2} x}{\tan x}\) dx + \(\frac{\sec ^{2} x}{\tan y}\)dy = 0
Integrating both sides, we get
∫ \(\frac{\sec ^{2} x}{\tan x}\) dx + ∫ \(\frac{\sec ^{2} y}{\tan y}\)dy = 0
⇒ log|tan x| + log|tan y| = log C
⇒ log|tan x tan y| = log C
⇒ tan x tan y = C
which is the required solution, where x ≠ odd multiple of and x ∈ R.

Question 5.
(e^x + e^-x)dy – (e^x – e^-x)dx = 0
Solution:
We have:
(e^x + e^-x)dy = (e^x – e^-x)dx
⇒ dy = \(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\)dx
Integrating both sides, we get
∫ dy = ∫ \(\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\)dx
⇒ ∫ dy = ∫\(\frac{dt}{t}\),
where e^x + e^-x = t so that (e^x – e^-x) dx = dt.
⇒ y = log |t| + C
⇒ y – C = log|e^x + e^-x| (x ∈ R)
or y = log (e^x + e^-x) + C (∵ e^x, e^-x > 0)
which is the required solution.

Question 6.
\(\frac{dy}{dx}\) = (1 + x)²(1 + y²)
Solution:
\(\frac{dy}{dx}\) = (1 + x)²(1 + y²)
or \(\frac{d y}{1+y^{2}}\) = (1 + x²) dx
Integrating both sides, we get
∫ \(\frac{d y}{1+y^{2}}\) = ∫
⇒ tan^-1y = x + \(\frac{x^{3}}{3}\) + C,
which is the required equation.

Question 7.
y log y dx – x dy = 0
Solution:
y log y dx – x dy = 0
or y log y dx = x dy or \(\frac{dy}{ylogy}\) = \(\frac{dx}{x}\)
Integrating both sides, we get
∫ \(\frac{dy}{ylogy}\) = ∫\(\frac{dx}{x}\)
Putting log y = t, \(\frac{1}{y}\)dy = dt
So, ∫ \(\frac{dt}{t}\) = log x + log C
∴ log(log y) = log Cx
∴ log y = Cx
or y = e^Cx is the required Solution.

Question 8.
x⁵\(\frac{dy}{dx}\) = – y⁵
Solution:

Putting – 4C = C. This is the required solution.

Question 9.
\(\frac{dy}{dx}\) = sin^-1x
Solution:
\(\frac{dy}{dx}\) = sin^-1x
or dy = sin^-1x
Integrating both sides, we get
∫ dy = ∫sin^-1 x dx + C
or y = ∫(sin^-1 x). 1 dx + C
Integrating by parts, taking sin^-1x as first function, we get

Putting this value of I₁ in (1), we get
y = x sin^-1x + \(\sqrt{1-x^{2}}\) + C
∴ The Solution is y = x sin^-1x + \(\sqrt{1-x^{2}}\) + C.

Question 10.
e^xtan y dx + (1 – e^x) sec²y dy = 0
Solution:
e^x tan y dx + (1 – e^x) sec²y dy = – e^x tan y dx = 0
or (1 – e^x) sec²y dy = – e^x tan y dx
Dividing by (1 – e^x) tan, we get
\(\frac{\sec ^{2} y}{\tan y}\) dy = + \(\frac{-e^{x}}{1-e^{x}}\)dx
Integrating both sides, we get
∫ \(\frac{\sec ^{2} y}{\tan y}\)dy = ∫\(\frac{-e^{x}}{1-e^{x}}\)dx
∴ log tan y = log (1 – e^-x) + log C
= log C(1 – e^-x)
∴ tan y = C(1 – e^-x) is the required solution.

For each of the differential equations in questions from 11 to 14, find a particular solution satisfying the given condition:

Question 11.
(x³ + x² + x + 1)\(\frac{dy}{dx}\) = 2x² + x; y = 1, when x = 0
Solution:
(x³ + x² + x + 1)\(\frac{dy}{dx}\) = 2x² + x
or (x³ + x² + x + 1)dy = (2x² + x)dx
or dy = \(\frac{2 x^{2}+x}{x^{3}+x^{2}+x+1}\) dx
Integrating both sides, we get

⇒ 2x² + x = A(x² + 1) + (Bx + C)(x + 1)
= A(x² + 1) + B(x² + x) + C(x + 1) ………….. (2)
Put x = – 1 in (2), we get
2 – 1 = A(1 + 1) ⇒ A = \(\frac{1}{2}\)
Comparing the coefficients of x² and x, we get
2 = A + B and 1 = B + C.
∴ B = 2 – A = 2 – \(\frac{1}{2}\) = \(\frac{3}{2}\).
C = 1 – B = 1 – \(\frac{3}{2}\) = – \(\frac{1}{2}\).

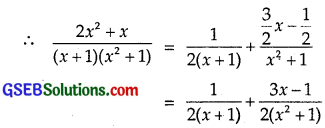
Therefore, from (1), we get

We have y = 1, when x = 0.
Putting these values in (3), we get
1 = \(\frac{1}{2}\) log 1 + \(\frac{3}{4}\) log 1 – \(\frac{1}{2}\)tan^-10 + C ……………. (3)
[Note : for integrating ∫ \(\frac{2 x}{x^{2}+1}\)dx, put x² + 1 = t
We have y = 1, when x = 0.
Putting these values in (3), we get
1 = \(\frac{1}{2}\) log 1 + \(\frac{3}{4}\) log 1 – \(\frac{1}{2}\)tan^-10 + C
= 0 + C ⇒ C = 1.
Thus, the solution is

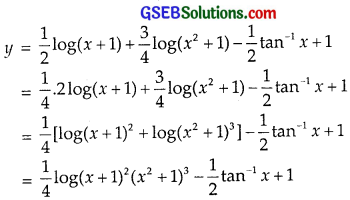
This is the required particular solution.

Question 12.
x(x² – 1)\(\frac{dy}{dx}\) = 1; y = 0, when x = 2
Solution:

Question 13.
cos(\(\frac{dy}{dx}\)) = a; (a ∈ R), y = 2, when x = 0
Solution:

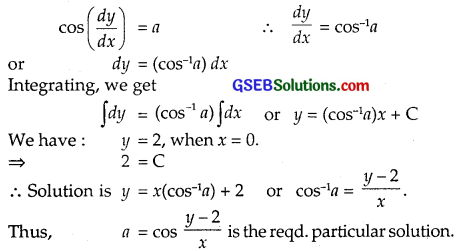
Question 14.
\(\frac{dy}{dx}\) = y tan x; y = 1, when x = 0
Solution:
\(\frac{dy}{dx}\) = y tan x or \(\frac{dy}{y}\) = tan x dx
Integrating, we get
∫ \(\frac{dy}{y}\) = ∫ tan x dx
⇒ log y = – log cos x + log C
or log y + log cos x = log C
∴ y cos x = C
Putting y = 1, x = 0 and ⇒ C = 1.
∴ y cos x = C
Putting y = 1, x = 0 ⇒ C = 1.
∴ y cos x = 1
or y = sec x is the required particular solution.

Question 15.
Find the equation of the curve passing through the point (0, 0) and whose differential equation is y’ = e^x sin x.
Solution:
y’ = e^xsin x or \(\frac{dy}{dx}\) = e^xsin x
∴ dy = e^x sin x dx
Integrating both sides, we get
∫ dy = ∫e^x sin x dx
Integrating by parts, taking e^x as the first function, we get
y = e^x(- cos x) – ∫e^x sin x dx
= – e^xcos x + ∫e^xcos x dx
Again integrating by parts, taking e^x as first function, we get
y = – e^x cos x + e^x sin x – ∫e^x sin x dx
⇒ y = – e^x cos x + e^x sin x – ∫dy
⇒ y = – e^x cos x + e^x sin x + C
∴ y = \(\frac{e^{x}}{2}\)[- cos x + sin x] + C
Put x = 0, y = 0.
0 = – \(\frac{1}{2}\) + C ∴ C = \(\frac{1}{2}\).
∴ Solution is y = \(\frac{e^{x}}{2}\)(sin x – cos x) + \(\frac{1}{2}\)
Which is the required equation of the curve.

Question 16.
If for the differential equation xy\(\frac{dy}{dx}\) = (x + 2)(y + 2), find the solution curve passing through the point (1, – 1).
Solution:
The differential equation is xy\(\frac{dy}{dx}\) = (x + 2)(y + 2)
or xy dy = (x + 2)(y + 2)dx
Dividing by x(y + 2), we get
\(\frac{y}{y+2}\)dy = \(\frac{x+2}{x}\)dx
Integrating, we get

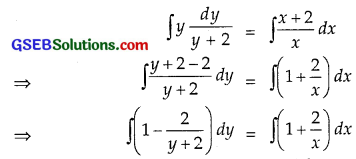
⇒ y – 2 log (y + 2) = x + 2 log x + C
The curve passes through (1, – 1)
∴ – 1 – 2 log 1 = 1 + 2 log 1 + C
⇒ – 1 = 1 + C [log 1 = 0]
∴ C = – 2.
Putting C = – 2, we get
y – 2 log (y + 2) = x + 2 log x – 2
or y – x = 2[log (y + 2) + log x] – 2
= 2 log x (y + 2) – 2
∴ Solution curve is y = x + 2 log x (y + 2) – 2.

Question 17.
Find the equation of the curve passing through the point (0, – 2) given that at any point (x, y) on the curve,
the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
Solution:
Slope of tangent to the curve at (x, y) = \(\frac{dy}{dx}\).
We are given: y(\(\frac{dy}{dx}\)) = x
∴ ydy = xdx
Integrating, we get
\(\frac{y^{2}}{2}\) = \(\frac{x^{2}}{2}\) + C
or y² = x² + 2C.
The curve passes through (0, – 2).
∴ 4 = 0 + 2C.
∴ 2C = 4.
∴ Equation of the curve is
y² = x² + 4 or y² – x² = 4.

Question 18.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (- 4, – 3).
Find the equation of the curve given that it passes through (- 2, 1).
Solution:
Slope of the tangent to the curve = \(\frac{dy}{dx}\)
Slope of the line joining (x, y) and (- 4, – 3) = \(\frac{y+3}{x+4}\)
We are given: \(\frac{dy}{dx}\) = 2(\(\frac{y+3}{x+4}\))
∴ dy = \(\frac{2(y+3)}{x+4}\) dx
Dividing by y + 3, we get
∴ \(\frac{dy}{y+3}\) = \(\frac{2}{x+4}\)dx
Integrating, we get
∫ \(\frac{dy}{y+3}\) = 2∫\(\frac{dx}{x+4}\)
or log(y + 3) = 2 log (x + 4) + log C
or log (y + 3) – log (x + 4)² = log C
i.e; log \(\frac{y+3}{(x+4)^{2}}\) = C ∴ \(\frac{y+3}{(x+4)^{2}}\) = C.
The curve passes through (- 2, 1).
∴ \(\frac{1+3}{(-2+4)^{2}}\) = C = \(\frac{4}{4}\) = 1.
∴ Equation of the curve is \(\frac{y+3}{(x+4)^{2}}\) = 1.
or y + 3 = (x + 4)² or y = (x + 4)² – 3.

Question 19.
The volume of a spherical balloon, being inIated, changes at a constant rate.
If initially its radius is 3 units and after 3 seconds it is 6 units, find the radius of balloon after t seconds.
Solution:
Let V be the volume of the balloon.

Putting values of k and C in (1), we get

Question 20.
In a bank, principal increases at the rate of r% per year. Find the value of r, if ₹100 double itself in 10 years (log 2 = 0.6931).
Solution:
Let p be the principal an rate of interest = r%.

∴ r = 10 × 0.6931 = 6.931.
Thus, the value of r = 6.931.

Question 21.
In a bank, principal increases at the rate of 5% per year.
An amount of ₹1000 is deposited with this bank. How much will it worth after 10 years (e^0.5 = 1.648)?
Solution:
Let p be the principal and Rate of interest is 5%.
∴ \(\frac{dp}{dt}\) = \(\frac{5}{100}\)p
∴ \(\frac{dp}{p}\) = 0.05 dt
Integrating, we get log p = 0.05 t + log C
or log p – log C = 0.05 t or log \(\frac{p}{C}\) = 0.05 t.
\(\frac{p}{C}\) = e^0.005t ∴ p = Ce^0.005t …………… (1)
Initially p = ₹1000, t = 0
∴ 1000 = C e⁰ = C
∴ C = 1000.
Putting this value in (1), we get
p = 1000 e^0.005t
When t = 10, p = 1000 e^0.005×10 = 1000 e^0.5
p = 1000 × 1.648 [∵ e^0.5 = 1.648]
= 1648
After 10 years, ₹1000 will amount to ₹1648.

Question 22.
In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours.
In how many hours, will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?
Solution:
Let y denote the number of bacteria at any instant t.
Then, according to the problem,
\(\frac{dy}{dt}\) ∝ y
⇒ \(\frac{dy}{y}\) = k dt ……………… (1)
where k is the constant of proportionality, taken to be positive. On integrating (1), we get
log y = kt + C ………………. (2)
where C is a parameter.
Let y₀ be the initial number of bacteria, i.e., at t = 0.
Using this in (2), we get C = log y₀.
So, we have: log y = kt + log y₀
⇒ log \(\frac{y}{y_{0}}\) = kt
According to the problem,
y = (y₀ + \(\frac{10}{100}\)y₀) = \(\frac{11 y_{0}}{10}\), when t = 2
So, from (3) we get,

Le the number of bacteria becomes from 1,00,000 to 2,00,000 in t₁ hours i.e; y = 2y₀, when t = t₁ hours.
Using (5) we get,

Question 23.
The general solution of the differential equation \(\frac{dy}{dx}\) = e^x+y is
(A) e^x + e^-y = c
(B) e^x + e^y = c
(C) e^-x + e^y = c
(D) e^-x + e^-y = c
Solution:
\(\frac{dy}{dx}\) = e^x+y = e^x.e^y
dy = e^x.e^y dx
Dividing by e^y, we get
e^-ydy = e^xdx
Integrating, we get
∫ e^-y dy = ∫ e^x dx
or – e^-y = e^-x – c = e^x + e^-y = c.
∴ Part (A) is the correct answer.