Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 11 Algebra Ex 11.5 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 11 Algebra Ex 11.5
Question 1.
State which of the following are equations (with a variable). Give a reason for your answer. Identify the variable from the equations with a variable.
(a) 17 = x + 7
(b) (t – 7) > 5
(c) \(\frac { 4 }{ 2 }\) = 2
(d) (7 × 3) – 19 = 8
(e) 5 × 4 – 8 = 2x
(f) x – 2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 × 5) – (12 × 4)
(j) 7 = (11 × 2) + p
(k) 20 = 5y
(l) \(\frac { 3q }{ 2 }\) < 5
(m) z + 12 > 24
(n) 20 – (10 – 5) = 3 x 5
(o) 7 – x = 5
Solution:
(a) It is an equation. It has a variable x.
(b) It is not an equation. There is no sign of equality (=).
(c) It is not an equation. It has no variable.
(d) It is not an equation. It has no variable.
(e) It is an equation. It has a variable x.
(f) It is an equation. It has a variable x.
(g) It is not an equation. It has no sign of equality (=).
(h) It is an equation. It has a variable n.
(i) It is not an equation. It has no variable.
(j) It is an equation. It has a variable p.
(k) It is an equation. It has a variable y.
(l) It is not an equation.’ It has no sign of equality (=).
(m) It is not an equation. It has no sign of equality (=).
(n) It is not an equation. It has no variable.
(o) It is an equation. It has a variable x.
![]()
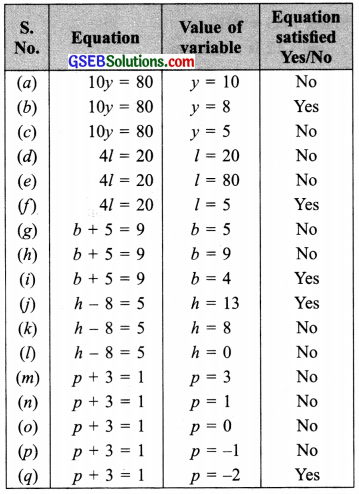
Question 2.
Complete the entries in the 4th column of the table.

Answer:
![]()
Question 3.
Pick out the solution from the values given in the bracket next to each equation. Show that the other values do not satisfy the equation.
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, -5)
(d) \(\frac { q }{ 2 }\)= 7 (7, 2, 10, 14)
(e) r – 4 = 0 (4, -4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
Solution:
(a) 5m = 60:
For m = 10, we have: LHS = 5 × 10 = 50 and
RHS 60
Since, LHS ≠ RHS
∴ m = 10 is not a solution.
For m = 5, we have: LHS = 5 × 5 = 25 and
RHS = 60
Since, LHS ≠ RHS
∴ m = 5 is not a solution.
For m = 12, we have: LHS = 5 × 12 = 60 and
RHS = 60
Since, LHS ≠ RHS.
∴ m = 12 is a solution.
For m = 15, we have: LHS = 5 × 15 = 75 and
RHS = 60
Since, LHS ≠ RHS
∴ m = 15 is not a solution
(b) n + 12 = 20:
For n = 12, LHS = 12 + 12 = 24 and RHS = 20
Since, LHS ≠ RHS
∴ n = 12 is not a solution.
For n = 8, we have: LHS = 8 +12 = 20 and
RHS = 20
Since, LHS = RHS
∴ n = 8 is a solution.
For n = 20, we have: LHS = 20 + 12 = 32 and
RHS = 20
Since LHS ≠ RHS
∴ n = 20 is not a solution.
For n = 0, we have: LHS =0 + 12 = 12 and
RHS = 20
Since, LHS ≠ RHS
∴ n = 0 is not a solution.
(c) p – 5 = 5
For p = 0, LHS = 0 – 5 = -5 and RHS = 5
Since, LHS ≠ RHS
∴ p = 0 is not a solution.
For p = 10, LHS = 10 – 5 = 5 and RHS = 5
Since, LHS = RHS
∴ p = 10 is a solution.
For p = 5, LHS = 5 – 5 = 0 and RHS = 5
Since, LHS ≠ RHS
∴ p = 5 is not a solution.
For p = -5, LHS = – 5 – 5 = -10 and RHS = 5
Since, LHS ≠ RHS
∴ p = -5 is not a solution.
(d) \(\frac { q }{ 2 }\) =7
For q = 7, LHS = \(\frac { 7 }{ 2 }\) and RHS = 7
Since, LHS ≠ RHS
∴ q = 7 is not a solution.
For q = 2, LHS = \(\frac { 2 }{ 2 }\) = 1 and RHS = 7
∵ LHS ≠ RHS
∴ q = 2 is not a solution.
For q = 10, LHS = \(\frac { 10 }{ 2 }\) = 5 and RHS = 7
∵ LHS ≠ RHS
∴ q = 10 is not a solution.
For q = 14, LHS = \(\frac { 14 }{ 2 }\) = 7 and RHS = 7
∵ LHS = RHS
∴ q = 14 is a solution.
(e) r – 4 = 0
For r = 4, LHS = 4 – 4 = 0 and RHS = 0
∵ LHS = RHS
∴ r = 4 is a solution.
For r = – 4, LHS = – 4 – 4 = -8 and RHS = 0
∵ LHS ≠ RHS
∴ r = – 4 is not a solution.
For r = 8, LHS = 8 – 4 = 4 and RHS = 0
∵ LHS ≠ RHS
∴ r = 8 is not a solution.
For r = 0, LHS = 0 – 4 = – 4 and RHS = 0
∵ LHS ≠ RHS
∴ r = 0 is not a solution.
(f) x + 4 = 2
For x = -2 , LHS = -2 + 4 = 2 and RHS = 2
∵ LHS = RHS
∴ x = -2 is a solution.
For x = 0 , LHS = 0 + 4 = 4 and RHS = 2
∵ LHS ≠ RHS
∴ x = 0 is not a solution.
For x = 2 , LHS = 2 + 4 = 6 and RHS = 2
∵ LHS ≠ RHS
∴ x = 2 is not a solution.
For x = 4 , LHS = 4 + 4 = 8 and RHS = 2
Since, LHS ≠ RHS
∴ x = 4 is not a solution.
![]()
Question 4.
(a) Complete the table and by inspection of the table, find the solution to the equation m + 10 =16

(b) Complete the table and by inspection of the table, find the solution to the equation 5t = 35.

(c) Complete the table and find the solution to the equation z/3 = 4 using the table.

(d) Complete the table and find the solution to the equation m – 7 = 3.

Solution:
(a) By inspection, we have:

∵ For m = 6, m + 10 = 16
∴ m = 6 is the solution to m + 10 = 16
(b) By inspection, we have:

∵ For t = 7, 5t = 35
∴ t = 7 is the solution to 5t = 35.
(c) By inspection, we have:

∵ For z = 12, \(\frac { z }{ 2 }\) = 4
∴ z = 12 is the solution to \(\frac { z }{ 3 }\) = 4
(d) By inspection, we have:

∵ For m = 10, m – 7 = 3
∴ m = 10 is the solution to m – 7 = 3
![]()
Question 5.
Solve the following riddles, you may yourself construct such riddles.
Who am I?
(i) Go round a square Counting every corner Thrice and no more! V Add the count to me To get exactly thirty-four!

(ii) For each day of the week Make an account from me If you make no mistake You will get twenty-three!
(iii) I am a special number Take away from me a six! A whole cricket team You will still be able to fix!

(iv) Tell me who I am I shall give a pretty clue! You will get me back If you take me out of twenty-two!
Solution:
(i) Suppose I am ‘x’
Since there are 4 comers of a square and each corner is counted thrice
∴ 4 × 3 = 12
According to the condition,
[myself] + 12 = 34
or x + 12 = 34
By inspection, we have
22 + 12 = 34
x = 22, Thus, I am 22.
(ii) There are 7 days in a week and let I am ‘x’.
∵ Accounting from JC for 7, the sum = 23
i.e. x + 7 = 23
∴ By inspection, we have 16 + 7 = 23
∴ x = 16, Thus, I am 16.
(iii) Let the special number be x and there are 11 members in a cricket team.
∵ [Special number] – 6 = [A cricket team] or x – 6 = 11
∴ By inspection, we have 17 – 6 = 11,
x = 17, Thus, I am 17.
(iv) Suppose I am ‘x’.
According to the problem,
22 – (myself) = (myself) or 22 – r = x
By inspection, we have: 22 – 11 = 11
∴ x = 11, Thus, I am 11.