Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 3 Playing With Numbers Ex 3.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 3 Playing With Numbers Ex 3.3
Question 1.
Using divisibility tests, determine which of the following numbers are divisible by 2; by 3; by 4; by 5; by 6; by 8; by 9; by 10; by 11 (say, yes or no):
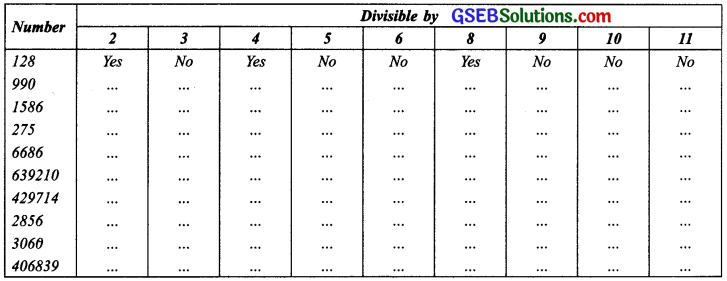
Answer:
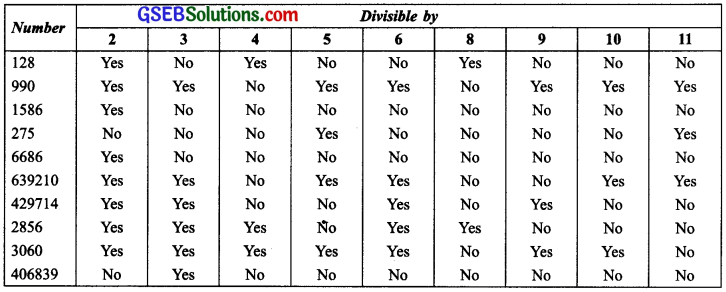
![]()
Question 2.
Using divisibility tests, determine which of the following numbers are divisible by 4; by 8:
(a) 572
(b) 726352
(c) 5500
(d) 6000
(e) 12159
(f) 14560
(g) 21084
(h) 31795072
(i) 1700
(j) 2150
Solution:

![]()
Question 3.
Using divisibility tests, determine which of following numbers are divisible by 6:
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
Answer:
(a) 297144

Since, 297144 is divisible by both 2 and 3,
297144 is divisible by 6.
(b) 1258

Since, 1258 is divisible by 2 but not by 3, therefore, it is not divisible by 6.
(c) 4335

Since, 4335 is divisible by 3 but not by 2, therefore, it is not divisible by 6.
(d) 61233

Since, 61233 is divisible by 3, but not by 2, therefore, 61233 is not divisible by 6.
(e) 901352

Since, 901352 is divisible by 2 but not by 3, therefore, 901352 is not divisible by 6.
(f) 438750

Since, 438750 is divisible by both 2 and 3, therefore 438750 is divisible by 6.
(g) 1790184

Since, 1790184 is divisible by 2 and 3 both, so, it is divisible by 6.
(h) 12583

Since 12583 is neither divisible by 2 nor by 3, therefore, it is not divisible by 6.
(i) 639210

Since, 639210 is dîvisible by 2 and 3 both, therefore, it is divisible by 6.
(j) 17852

Since, 17852 is divisible by 2 but not by 3, so it is not divisible by 6.
![]()
Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 11.
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001
(f) 901153
Solution:
(a) 5445
Sum of digits at odd places from the right = 5 + 4 = 9
Sum of the digits at even places from the right = 4 + 5 = 9
Difference of these two sums 9 – 9 = 0
5445 is divisible by 11.
(b) 10824
Sum of the digits at odd places from the right = 4 + 8 + 1 = 13
Sum of digits at even places from the right = 2 + 0 = 2
Difference of these two sums = 13 – 2 = 11
11 is a multiple of 11,
10824 is divisible by 11.
(c) 7138965
Sum of digits at odd places from the right = 5 + 9 + 3 + 7 = 24
Sum of digits at even places from the right = 6 + 8 + 1 = 15
Difference of these two sums = 24 – 15 = 9
9 is not a multiple of 11.
7138965 is not divisible by 11.
(d) 70169308
From the right, Sum of the digits at odd places = 8 + 3 + 6 + 0 = 17
Sum of the digits at even places = 0 + 9 + 1 + 7 = 17
Difference of these two sums = 17 – 17 = 0
70169308 is divisible by 11.
(e) 10000001
From the right Sum of the digits at odd places = 1 + 0 + 0 + 0 = 1
Sum of the digits at even places = 0 + 0 + 0 = 1
: The difference of these two sums = 1 – 1 = 0
10000001 is divisible by 11.
(f) 901153
From the right The sum of digits at odd places = 3 + 1 + 0 = 4
The sum of digits at even places 5 + 1 + 9 = 15
Difference of these two sums = 15 – 4 = 11,
which is a multiple of 11.
901153 is divisible by 11.
![]()
Question 5.
Write the smallest digit and the greatest digit in the blank space of each of the following numbers so that the number formed is divisible by 3:
(a) ………….. 6724
(b) 4765 …………. 2
Solution:
(a) ………….. 6724
Sum of the given digits = 6 + 7 + 2 + 4 = 19
Multiples of 3 greater than 19 are 21, 24, 27 and 30
21 – 19 = 2
24 – 19 = 5
27 – 19 = 8
30 – 19 = 11 (11 is not a digit)
The smallest required digit = 2
The greatest required digit = 8
(b) 4765 …………. 2
Sum of the given digits 4 + 7 + 6+ 5 +2 = 24,
which is a multiple of 3
The smallest required digit = 0
Next multiples of 3 are 27, 30, 33, 36
27 – 24 = 3
30 – 24 = 6
33 – 24 = 9
The largest required digit = 9
![]()
Question 6.
Write a digit in the blank space of each of the following numbers so that the number form ed is divisible by 11:
(a) 92 ………….. 389
(b) 8 ………….. 9484
Solution:
(a) 92 ………….. 389
We have:
Sum of the digits at odd places = 9 + 3 + 2 = 14
Sum of digits at even places = 8 + [Missing digitl +9 = [Missing digit] + 17
Difference of these sums = [Missing digit] + 17 – 14 = [Missing digit] + 3
For the given number to be divisible by 11 [Missing digit] + 3 11
Missing digit = 11 – 3 = 8
Thus, the number is 928389.
(b) 8 ………….. 9484
Sum of the digits at odd places = 4 + 4 + [Missing digit]
= [Missing digit] + 8
Sum of the digits at even places = 8 + 9 + 8 = 25
Difference of these sums = 25 – [(Missing digit) + 8]
= 25 – Missing digit – 8
= 17 – Missing digit
For the given number to be divisible by 11,
= 17 – Missing digit = 11
i.e. Missing digit 17 – 11 = 6
The given number is 869484.