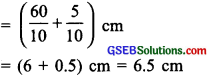Gujarat BoardĀ GSEB Textbook Solutions Class 6 Maths Chapter 8 Decimals Ex 8.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 8 Decimals Ex 8.1
Question 1.
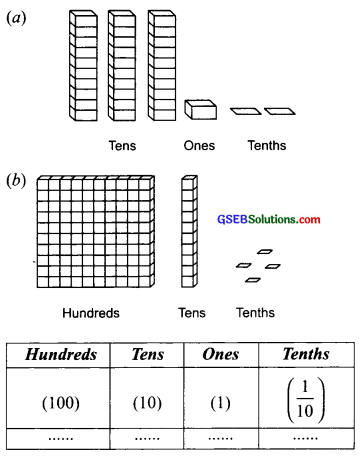
Write the following as numbers in the given table.
Solution:
(a) In the given figure there are:
3 towers (each of 10 units), one block (equal to 1 unit), and 2 small parts (each equal to 2 tenths). So, we can write in the given table as:
(b) In the figure, there are:
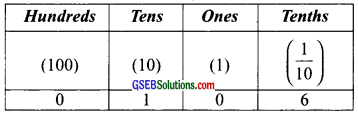
1 hundred, 1 ten, 0 units, and 4 tenths. So given table is written as:
Question 2.
Write the following decimals in the place value table.
(a) 19.4
(b) 0.3
(c) 10.6
(d) 205.9
Solution:
(a) 19.4
āµ 19.4 = 1 Ć 10 + 9 Ć 1 + 4 Ć \(\frac { 1 }{ 10 }\)
ā“ We have,
(b) 0.3
āµ 0.3 = 0 + \(\frac { 3 }{ 10 }\)
ā“ We have,
(c) 10.6
āµ 10.6 = 1 Ć 10 + 0 Ć 1 + 6 Ć \(\frac { 1 }{ 10 }\)
ā“ We have,
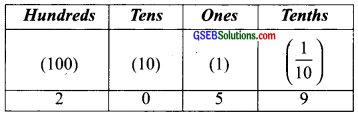
(d) 205.9
āµ 205.9 = 2 Ć 100+ 0 Ć 10 +5 Ć 1 +9 Ć \(\frac { 1 }{ 10 }\)
ā“ We have,
Question 3.
Write each of the following as decimals:
(a) Seven-tenths
(b) Two tens and nine-tenths
(c) Fourteen point six
(d) One hundred and two ones
(e) Six hundred point eight
Solution:
(a) Seven-tenths:
We have seven-tenths = 7 Ć \(\frac { 1 }{ 10 }\) = 0.7
(b) Two tens and nine-tenths:
We have, two tens and nine-tenths
= 2 Ć 10 + 9 Ć \(\frac { 1 }{ 10 }\) = 20 + \(\frac { 9 }{ 10 }\)
= 20 + 0.9 = 20.9
(c) Fourteen point six:
We have, fourteen point six = 14.6
(d) One hundred and two ones:
We have, one hundred and two = 1 hundred + 0 tens + 2 ones + 0 tenths
= 100 + 0 + 2 + \(\frac { 0 }{ 10 }\) = 102.0
(e) Six hundred point eight:
We have, 6 hundred points 8 = 600.8
Question 4.
Write each of the following as decimals:
(a) \(\frac { 5 }{ 10 }\)
(b) 3 + \(\frac { 7 }{ 10 }\)
(c) 200 + 60 + 5 + \(\frac { 1 }{ 10 }\)
(d) 70 + \(\frac { 8 }{ 10 }\)
(e) \(\frac { 88 }{ 10 }\)
(f) 4\(\frac { 2 }{ 10 }\)
(g) \(\frac { 3 }{ 2 }\)
(h) \(\frac { 2 }{ 5 }\)
(i) \(\frac { 12 }{ 5 }\)
(j) 3\(\frac { 3 }{ 5 }\)
(k) 4\(\frac { 1 }{ 2 }\)
Solution:
(a) \(\frac { 5 }{ 10 }\) = 0.5
(b) 3 + \(\frac { 7 }{ 10 }\) = 3 + 0.7 = 3.7
(c) 200 + 60 + 5 + \(\frac { 1 }{ 10 }\) = 265 + 0.1 = 265.1
(d) 70 + \(\frac { 8 }{ 10 }\) = 70 + 0.8 = 70.8
(e) \(\frac { 88 }{ 10 }\) = \(\frac{80+8}{10}\) = \(\frac { 80 }{ 10 }\) + \(\frac { 8 }{ 10 }\) = 8 + \(\frac { 8 }{ 10 }\) = 8.
(f) 4\(\frac { 2 }{ 10 }\) = 4 + 4\(\frac { 2 }{ 10 }\) = 4.2
(g) \(\frac { 3 }{ 2 }\)
Since, \(\frac { 3 }{ 2 }\) = \(\frac { 3 Ć 5 }{ 2 Ć 5 }\) = \(\frac { 15 }{ 10 }\) = \(\frac { 10 + 5 }{ 10}\)
= \(\frac { 10 }{ 10 }\) + \(\frac { 5 }{ 10 }\) = 1 + \(\frac { 5 }{ 10}\) = 1.5
Thus,\(\frac { 3 }{ 2 }\) = 1.5
(h) \(\frac { 2 }{ 5 }\)
Since, \(\frac { 2 }{ 5 }\) = \(\frac { 2 Ć 2 }{ 5 Ć 2 }\) = \(\frac { 4 }{ 10 }\) = 0.4
ā“ \(\frac { 2 }{ 5 }\) = 0.4
(i) \(\frac { 12 }{ 5 }\)
Since, \(\frac { 12 }{ 5 }\) Ć \(\frac { 2 }{ 2 }\) = \(\frac { 24 }{ 10 }\) = \(\frac { 20 + 4 }{ 10 }\) = \(\frac { 20 }{ 10 }\) + \(\frac { 4 }{ 10 }\)
= 2 + \(\frac { 4 }{ 10 }\) = 2.4
(j) 3\(\frac { 3 }{ 5 }\)
Since, 3\(\frac { 3 }{ 5 }\) = 3 + \(\frac { 3 }{ 5 }\) = 3 + \(\left(\frac{3}{5} \times \frac{2}{2}\right)\)
= 3 + \(\frac { 6 }{ 10 }\) = 3.6
(k) 4\(\frac { 1 }{ 2 }\)
Since, 4\(\frac { 1 }{ 2 }\) = 4 + \(\frac { 1 }{ 2 }\) = 4 + 4\(\frac { 1 Ć 5 }{ 2 Ć 5 }\)
= 4 + 4\(\frac { 5 }{ 10 }\) = 4.5
Question 5.
Write the following decimals as fractions. Reduce the fractions to the lowest form.
(a) 0.6
(b) 2.5
(c) 1.0
(d) 3.8
(e) 13.7
(f) 21.2
(g) 6-4
Note: To convert a decimal to a fraction, we have the following steps:
I. Count the number of digits in the decimal part.
II. Ignoring the decimal point, write all the given digits as the numerator of the fraction.
III. In the denominator write as many zeros after 1 as there are decimal places in the decimal fraction.
IV. Reduce the fraction, so obtained, to its simplest form.
Solution:
Question 6.
Express the following as cm using decimals,
(a) 2 mm
(b) 30 mm
(c) 116 mm
(d) 4 cm 2 mm
(e) 162 mm
(f) 83 mm
Solution:
(a) 2 mm:
āµ 10 mm = 1 cm or 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 2 mm = \(\frac { 1 }{ 10 }\) Ć 2 mm = \(\frac { 2 }{ 10 }\) cm = 0.2 cm
(b) 30 mm
āµ 10 mm = 1 cm or 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 30 mm = \(\frac { 1 }{ 10 }\) Ć 30 mm = \(\frac { 30 }{ 10 }\) cm = 3.0 cm
(c) 116 mm
āµ 10 mm = 1 cm or 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 116 mm = \(\frac { 1 }{ 10 }\) Ć 116 mm = \(\frac { 116 }{ 10 }\) cm
= \(\frac { 116 + 6 }{ 10 }\) cm = \(\left(\frac{110}{10}+\frac{6}{10}\right)\) cm
= \(\left(11+\frac{6}{10}\right)\) cm = 11.6 cm
(d) 4 cm 2 mm
We have : 4 cm 2 mm = 4 cm + 2 mm
= 4 cm + \(\frac { 2 }{ 10 }\) cm
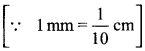
(e) 162 mm:
āµ 10 mm = 1 cm or 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 162 mm = \(\frac { 1 }{ 10 }\) Ć 162 cm = \(\frac { 162 }{ 10 }\) cm
= \(\frac { 162 + 2 }{ 10 }\) cm = 
(f) 83 mm:
āµ 10 mm = 1 cm or 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 83 mm = \(\frac { 1 }{ 10 }\) Ć 83 cm = \(\frac { 83 }{ 10 }\) cm
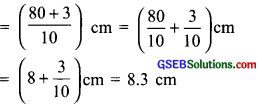
Question 7.
Between which two whole numbers on the number line are the given numbers lie? Which of these whole numbers is nearer the number?
(a) 0.8
(b) 5.1
(c) 2.6
(d) 6.4
(e) 9.1
(f) 4.9
Solution:
(a) 0.8:
0.8 lies between 0 and 1 and 1 are nearer to 0.8.
(b) 5.1:
5.1 lies between 5 and 6 and 5 are nearer to 5.1.
(c) 2.6:
2.6 lies between 2 and 3 and 3 are nearer to 2.6.
(d) 6.4:
6.4 lies between 6 and 7 and 6 are nearer to 6.4.
(e) 9.1:
9.1 lies between 9 and 10 and 9 are nearer to 9.1.
(f) 4.9:
4.9 lies between 4 and 5 and 5 are nearer to 4.9.
Question 8.
Show the following numbers on the number line.
(a) 0.2
(b) 1.9
(c) 1.1
(d) 2.5
Solution:
(a) 0.2
0.2 lies between 0 and 1
ā“ Divide the unit length between 0 and 1 into 10 equal parts and take 2 parts as shown below. A
(b) 1.9
1.9 lies between 1 and 2
ā“ Divide the unit length between 1 and 2 into 10 equal parts and take 9 parts as shown below:
Point B represents 1.9.
(c) 1.1
1.1 lies between 1 and 2. Divide the unit length between 1 and 2 into 10 equal parts and take 1 part as shown below:
Thus, point C represents 1.1.
(d) 2.5
2.5 lies between 2 and 3. Divide the unit length between 2 and 3 into 10 equal parts and take 5 parts as shown below:
Thus, point D represents 2.5.
Question 9.
Write the decimal number represented by the points A, B, C, D on the given number line.
Solution:
(i) Point A: Point A lies between 0 and 1. The unit distance between 0 and 1 is divided into 10 equal parts. Point A stands at the 8th part.
Thus, 0.8 is represented by A
(ii) Point B: Point B lies between 1 and 2. The unit distance between 1 and 2 is divided into 10 equal parts and point B is at the 3rd part.
Thus, 1.3 is represented by B.
(iii) Point C: The point C lies between 2 and 3. The unit distance between 2 and 3 is divided into 10 equal parts and C is at the 2nd part. Thus, 2.2 is represented by C.
(iv) Point D: The point D lies between 2 and 3. The distance between 2 and 3 is divided into 10 equal parts and the 9 parts have been taken.
ā“ 2.9 is represented by D.
Question 10.
(a) The length of Ramesh’s notebook is 9 cm 5 mm. What will be its length in cm?
(b) The length of a young gram plant is 65 mm. Express its length in cm.
Solution:
(a) Length of Rameshās notebook = 9 cm 5 mm
But 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 5 mm = 5 Ć \(\frac { 1 }{ 10 }\) cm = \(\frac { 5 }{ 10 }\) cm = 0.5 cm
Now 9 cm 5 mm = 9.5 cm
Thus, the length of the notebook = 9.5 cm
(b) āµ 1 mm = \(\frac { 1 }{ 10 }\) cm
ā“ 65 mm = 65 Ć \(\frac { 1 }{ 10 }\) cm
= \(\frac { 65 }{ 10 }\) cm = \(\frac { 65 + 5 }{ 10 }\) cm
