Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 3 Data Handling Ex 3.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 3 Data Handling Ex 3.1
![]()
Question 1.
Find the range of heights of any ten students of your class.
Solution:
Let the heights of ten students are as follows:
118 cm, 111 cm, 114 cm, 120 cm, 110 cm,
115 cm, 119 cm, 118 cm, 117 cm, 113 cm
Writing the heights in ascending order, we have:
110 cm, 111 cm, 113 cm, 114 cm, 115 cm,
117 cm, 118 cm, 118 cm, 119 cm, 120 cm
∴ Maximum height = 120 cm
Minimum height = 110 cm
∴ Range = Maximum height – Minimum height = 120 cm – 110 cm = 10 cm
Question 2.
Organise the following marks in a class assessment, in a tabular form.
4, 6, 7, 5, 3, 5, 4, 5, 2, 6,
2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) Which number is the highest?
(ii) Which number is the lowest?
(iii) What is the range of the data?
(iv) Find the arithmetic mean.
Solution:
Writing the given data (marks) in a tabular form, we have:

(i) The highest number = 9
(ii) The lowest number = 1
(iii) The range = Highest number – Lowest number = 9 – 1 = 8
(iv)

Thus, the mean marks = 5
![]()
Question 3.
Find the mean of the first five whole numbers.
Solution:
First five whole numbers are: 0, 1, 2, 3 and 4
Sum = 0+1+2 + 3 + 4 = 10
∴ Mean = ![]()
= \(\frac { 10 }{ 5 }\)
= 2
Question 4.
A cricketer scores the following runs in eight innings:
58, 76, 40, 35, 46, 45, 0, 100
Find the mean score.
Solution:

Therefore, the mean score = 50.
Question 5.
Following table shows the points of each player scored in four games:

Now answer the following questions:
(i) Find the mean to determine A’s average number of points scored per game.
(ii) To find the mean number of points per game for C, would you divide the total points by 3 or by 4? Why?
(iii) B played in all the four games. How would you find the mean?
(iv) Who is the best performer?
Solution:
(i) Mean = 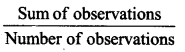
= \(\frac { 14+16+10+10 }{ 4 }\)
= \(\frac { 50 }{ 4 }\)
= 12.5
∴ A’s average score per game is 12.5.
(ii) Since C played only 3 games [He did not play the 3rd game].
∴Total will be divided by 3.
(iii) 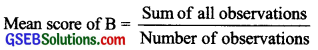
= \(\frac { 0+8+6+4 }{ 4 }\)
= \(\frac { 18 }{ 4 }\)
= 4.5
Thus, the average number of points scored by B is 4.5.
(iv) Mean score of
C = 
= \(\frac { 8+11+13 }{ 3 }\)
= \(\frac { 32 }{ 3 }\)
= 10.67
Thus, mean (average) number of points scored by C is 10.67. Obviously the average of ‘A’ is the highest. Thus A is the best player.
![]()
Question 6.
The marks (out of 100) obtained by a group of students in a science test are 85, 76, 90, 85, 39, 48, 56, 95, 81 and 75. Find the:
(i) Highest and the lowest marks obtained by the students.
(ii) Range of the marks obtained.
(iii) Mean marks obtained by the group.
Solution:
Writing the given marks in ascending order, we have:
39, 48, 56, 75, 76, 81, 85, 85, 90, 95
(i) Highest marks = 95
Lowest marks = 39
(ii) Range = Highest marks Lowest marks = 95 – 39 = 56
(iii)

Thus, mean marks obtained by the group is 73.
Question 7.
The enrolment in a school during six consecutive years was as follows:
1555, 1670, 1750, 2013, 2540, 2820
Find the mean enrolment of the school for this period.
Solution:
Sum of enrolments
= 1555 + 1670 + 1750 + 2013 + 2540 + 2820 = 12348

Thus, the mean enrolment is 2058 per year.
Question 8.
The rainfall {in mm) in a city on 7 days of a certain week was recorded as follows:

(i) Find the range of the rainfall in the above data.
(ii) Find the mean rainfall for the week.
(iii) On how many days was the rainfall less than the mean rainfalYl
Solution:
(i) Range = Highest rainfall – Lowest rainfall
= 20.5 – 0.0 = 20.5 mm
(ii)

∴ Mean rainfall = 5.9 mm
(iii) From the table, we find that on 5 days [Monday, Wednesday, Thursday, Saturday and Sunday] the rainfall was less than the mean rainfall.
![]()
Question 9.
The heights of 10 girls were measured in cm and the results are as follows:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141
(i) What is the height of the tallest girl?
(ii) What is the height of the shortest girl?
(iii) What is the range of the data?
(iv) What is the mean height of the girls?
(v) How many girls have heights more than the mean height?
Solution:
Writing the heights in ascending order, we have:
128, 132, 135, 139, 141, 143, 146, 149, 150, 151
(i) Height of the tallest girl = 151 cm
(ii) Height of the shortest girl 128 cm
(iii) Range = Highest height – Lowest height
= 151 cm – 128 cm
= 23 cm
(iv)

Thus, the mean height of the girls is 141.4 cm.
(v) Since, 143 cm, 146 cm, 149 cm, 150 cm and 151 cm are greater than 141.4.
∴ The heights of 5 girls are more than the mean height.