Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 2 Fractions and Decimals InText Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 2 Fractions and Decimals InText Questions
![]()
Try These (Page 34)
Question 1.
Find:
(a) \(\frac { 2 }{ 7 }\) x 3
(b) \(\frac { 9 }{ 7 }\) x 6
(c) 3 x \(\frac { 1 }{ 8 }\)
(d) \(\frac { 13 }{ 11 }\) x 6
If the product is an improper fraction express it as a mixed fraction.
Solution:
(a) \(\frac { 2 }{ 7 }\) x 3
= \(\frac { 2×3 }{ 7 }\)
= \(\frac { 6 }{ 7 }\)
(b) \(\frac { 9 }{ 7 }\) x 6
= \(\frac { 9×6 }{ 7 }\)
= \(\frac { 54 }{ 7 }\)
= 7\(\frac { 5 }{ 7 }\)
(c) 3 x \(\frac { 1 }{ 8 }\)
= \(\frac { 3×1 }{ 8 }\)
= \(\frac { 3 }{ 8 }\)
(d) \(\frac { 13 }{ 11 }\) x 6
= \(\frac { 13×6 }{ 11 }\)
= \(\frac { 78 }{ 11 }\)
= 7\(\frac { 1 }{ 11 }\)
![]()
Question 2.
Represent pictorially: 2 x \(\frac { 2 }{ 5 }\) = \(\frac { 4 }{ 5 }\)
Solution:

or 2 x \(\frac { 2 }{ 5 }\) = \(\frac { 4 }{ 5 }\)
Try These (Page 34)
Question 1.
Find: (i) 5 x 2\(\frac { 3 }{ 7 }\)
(ii) 1\(\frac { 4 }{ 9 }\) x 6
Solution:
(i) 5 x 2\(\frac { 3 }{ 7 }\)
= 5 x \(\frac { 17 }{ 7 }\)
= \(\frac { 85 }{ 7 }\)
= 12\(\frac { 1 }{ 7 }\)
(ii) 1\(\frac { 4 }{ 9 }\) x 6
= \(\frac { 13 }{ 9 }\) x 6
= 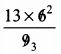
= \(\frac { 13×2 }{ 3 }\)
= \(\frac { 26 }{ 3 }\)
= 8\(\frac { 2 }{ 3 }\)
Try These (Page 35)
Question 1.
Can you tell, what is
(i) \(\frac { 1 }{ 2 }\) of 10?
(ii) \(\frac { 1 }{ 4 }\) of 16?
(iii) \(\frac { 2 }{ 5 }\) of 25?
Solution:
(i) \(\frac { 1 }{ 2 }\) of 10
= \(\frac { 1 }{ 2 }\) x 10
= \(\frac { 1×10 }{ 2 }\)
= 5
(ii) \(\frac { 1 }{ 4 }\) of 16
= \(\frac { 1 }{ 4 }\) x 16
= \(\frac { 1×16 }{ 4 }\)
= 4
(iii) \(\frac { 2 }{ 5 }\) of 25
= \(\frac { 2 }{ 5 }\) x 25
= \(\frac { 2×25 }{ 5 }\)
= 10
![]()
Try These (Page 39)
Question 1.
Fill in these boxes:
(i) \(\frac { 1 }{ 2 }\) x \(\frac { 1 }{ 7 }\) = \(\frac { 1×1 }{ 2×7 }\) = ![]()
(ii) \(\frac { 1 }{ 5 }\) x \(\frac { 1 }{ 7 }\) = ![]() =
= ![]()
(iii) \(\frac { 1 }{ 7 }\) x \(\frac { 1 }{ 2 }\) = ![]() =
= ![]()
(iv) \(\frac { 1 }{ 7 }\) x \(\frac { 1 }{ 5 }\) = ![]() =
= ![]()
Solution:

Try These (Page 40)
Question 1.
Find: \(\frac { 1 }{ 3 }\) x \(\frac { 4 }{ 5 }\); \(\frac { 2 }{ 3 }\) x \(\frac { 1 }{ 5 }\)
Solution:
(i) \(\frac { 1 }{ 3 }\) x \(\frac { 4 }{ 5 }\) = \(\frac { 1×4 }{ 3×5 }\) = \(\frac { 4 }{ 15 }\)
(ii) \(\frac { 2 }{ 3 }\) x \(\frac { 1 }{ 5 }\) = \(\frac { 2×1 }{ 3×5 }\) = \(\frac { 2 }{ 15 }\)
Try These (Page 40)
Question 1.
Find: \(\frac { 8 }{ 3 }\) x \(\frac { 4 }{ 7 }\); \(\frac { 3 }{ 4 }\) x \(\frac { 2 }{ 3 }\)
Solution:
(i) \(\frac { 8 }{ 3 }\) x \(\frac { 4 }{ 7 }\) = \(\frac { 8×4 }{ 3×7 }\) = \(\frac { 32 }{ 21 }\)
(ii) \(\frac { 3 }{ 4 }\) x \(\frac { 2 }{ 3 }\) = \(\frac { 3×2 }{ 4×3 }\) = \(\frac { 1×1 }{ 2×1 }\) = \(\frac { 1 }{ 2 }\)
![]()
Think, Discuss and Write (Page 44)
Question 1.
(i) Will the reciprocal of a proper fraction be again a proper fraction?
(ii) Will the reciprocal of an improper fraction be again an improper fraction!
Solution:
(i) No, the reciprocal of a proper fraction is an improper fraction.
(ii) No, the reciprocal of an improper fraction is a proper fraction.
Now, we can say that
(a) 1 ÷ \(\frac { 1 }{ 2 }\)
= 1 x \(\frac { 2 }{ 1 }\)
= 1 x reciprocal of \(\frac { 1 }{ 2 }\)
(b) 3 ÷ \(\frac { 1 }{ 4 }\)
= 3 x \(\frac { 4 }{ 1 }\)
= 3 x reciprocal of \(\frac { 1 }{ 4 }\)
(c) 3 ÷ \(\frac { 1 }{ 2 }\) = _____ = _____
3 x \(\frac { 1 }{ 2 }\) = 3 x \(\frac { 2 }{ 1 }\) reciprocal of \(\frac { 1 }{ 2 }\)
And, 2 ÷ \(\frac { 3 }{ 4 }\) = 2 x reciprocal of \(\frac { 3 }{ 4 }\)
= 2 x \(\frac { 4 }{ 3 }\)
(d) 5 ÷ \(\frac { 2 }{ 9 }\) = 5 x _____ = _____
∴ 5 ÷ \(\frac { 2 }{ 9 }\) = 5 x \(\frac { 9 }{ 2 }\) = 5 x reciprocal of \(\frac { 2 }{ 9 }\)
Remember:
I. When the product of two fractions is unity, then each is called the “reciprocal of the other”.
II. When unity is divided by a fraction, then the quotient is the “reciprocal” of that fraction.
Try These (Page 45)
Question 1.
Find:
(i) 7 ÷ \(\frac { 2 }{ 5 }\)
(ii) 6 ÷ \(\frac { 4 }{ 7 }\)
(iii) 2 ÷ \(\frac { 8 }{ 9 }\)
Solution:

Try These (Page 45)
Question 1.
Find:
(i) 6 ÷ 5\(\frac { 1 }{ 3 }\)
(ii) 7 ÷ 2\(\frac { 4 }{ 7 }\)
Solution:
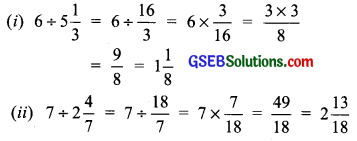
![]()
Try These (Page 45)
Question 1.
Find:
(i) \(\frac { 3 }{ 5 }\) ÷ \(\frac { 1 }{ 2 }\)
(ii) \(\frac { 1 }{ 2 }\) ÷ \(\frac { 3 }{ 5 }\)
(iii) 2\(\frac { 1 }{ 2 }\) ÷ \(\frac { 3 }{ 5 }\)
(iv) 5\(\frac { 1 }{ 6 }\) ÷ \(\frac { 9 }{ 2 }\)
Solution:

Try These (Page 50)
Question 1.
Find:
(i) 2.7 x 4
(ii) 1.8 x 1.2
(iii) 2.3 x 4.35
Solution:
(i) 2.7 x 4
∵ 27 x 4 = 108 and there is one digit to the right of the decimal point in 27.
∴ 2.7 x 4 = 10.8
(ii) 1.8 x 1.2
∵ 18 x 12 = 216 and number of digits to the right of decimal point is (1 + 1), i.e. 2.
∴ 1.8 x 1.2 = 2.16
(iii) 2.3 x 4.35
∵ 23 x 435 = 10005 and there are 1+2, i.e.
∴ digits to the right of decimal point.
∴ 2.3 x 4.35 = 10.005
![]()
Question 2.
Arrange the products obtained in Question 1 in descending order.
Solution:
The products are: 10.8, 2.16, 10.005.
Comparing 10.8 and 10.005, we have:
10 = 10, 8 > 0, i.e. 10.005 < 10.8
Here, the smallest number = 2.16
and, the largest number = 10.8
Thus, the required descending order is: 10.8, 10.005, 2.16.
Try These (Page 51)
Question 1.
Find:
(i) 0.3 x 10
(ii) 1.2 x 100
(iii) 56.3 x 1000
Solution:
(i) 0.3 x 10
∵ There is 1 zero in 10.
∴ The decimal point is shifted to the right by 1 place.
Thus, 0.3 x 10 = 3
(ii) 1.2 x 100
∵ There are 2 zeros in 100.
∴ The decimal point is shifted to the right by 2 places.
Thus, 1.2 x 100 = 120
(iii) 56.3 x 1000
∵ There are three zeros in 1000.
∴ The decimal point is shifted to the right by 3 places.
Thus, 56.3 x 1000 = 56300
![]()
Try These (Page 53)
Question 1.
Find:
(i) 235.4 ÷ 10
(ii) 235.4 + 100
(iii) 235.4 ÷ 1000
Solution:
(i) 235.4 ÷ 10
Since, there is one zero in 10.
∴The decimal point in the quotient is shifted to the left by one place.
∴ 235.4 ÷ 10 = 23.54
(ii) 235.4 ÷ 100
Since, there are two zeros in 100
∴ The decimal point in the quotient is shifted to the left by two places.
∴ 235.4 ÷ 100 = 2.354
(iii) 235.4 ÷ 1000
Since, there are three zeros in 1000.
∴ The decimal point in the quotient is shifted to the left by three places.
∴ 235.4 ÷ 1000 = 0.2354
Try These (Page 53)
Question 1.
Find:
(i) 35.7 ÷ 3
(ii) 25.5 ÷ 3
Solution:
(i) 35.7 ÷ 3
Since, \(\frac { 357 }{ 3 }\) =119 and there is one digit in the decimal part of the given decimal number.
∴ The decimal point is placed in the quotient after one digit from the right most digit.
∴ 35.7 ÷ 3 = 11.9
(ii) 25.5 ÷ 3
Since, 255 ÷ 3 = 85 and there is one digit in the decimal part of the given decimal number.
∴ The decimal is placed in the quotient after one digit from the right most digit.
∴ 25.5 ÷ 3 = 8.5
![]()
Try These (Page 53)
Question 1.
Find:
(i) 43.15 ÷ 5
(ii) 82.44 ÷ 6
Solution:
(i) 43.15 ÷ 5
Since 4315 ÷ 5 = 863 and there are two digits in the decimal part of the given decimal number.
∴ Place the decimal point in 863 such that there are two digits to its right.
∴ 43.15 ÷ 5 = 8.63
(ii) 82.44 + 6
Since 8244 ÷ 6 = 1374 and there are two digits in the decimal part of the given decimal number.
∴ Place the decimal point in 1374 such that there are two digits to its right.
∴ 82.44 ÷ 6 = 13.74
Try These (Page 53)
Question 1.
Find:
(i) 15.5 ÷ 5
(ii) 126.35 ÷ 7
Solution:
(i) 15.5 ÷ 5
Since 155 ÷ 5 = 31 and there is one digit in the decimal part of the given decimal number.
∴ Place the decimal point in 31 such that there is one digit to its right.
∴ 15.5 ÷ 5 = 3.1
(ii) 126.35 ÷ 7
Since 12635 ÷ 7 = 1805 and there are two digits in the decimal part of the given decimal number.
∴ Place the decimal point in 1805 such that there are two digits to its right.
∴ 126.35 ÷ 7 = 18.05
![]()
Try These (Page 54)
Question 1.
Find:
(i) \(\frac { 7.75 }{ 0.25 }\)
(ii) \(\frac { 42.8 }{ 0.02 }\)
(iii) \(\frac { 5.6 }{ 1.4 }\)
Solution:
(i) \(\frac { 7.75 }{ 0.25 }\)
since, 7.75 = \(\frac { 775 }{ 100 }\) and 0.25 = \(\frac { 25 }{ 100 }\)
∴ 7.75 ÷ 0.25 = \(\frac { 775 }{ 100 }\) ÷ \(\frac { 25 }{ 100 }\)
= \(\frac { 775 }{ 100 }\) x \(\frac { 100 }{ 25 }\)
= \(\frac { 775 }{ 25 }\)
= 31
∴ \(\frac { 7.75 }{ 0.25 }\) = 31
(ii) \(\frac { 42.8 }{ 0.02 }\)
since, 42.8 = \(\frac { 428 }{ 10 }\) and 0.25 = \(\frac { 2 }{ 100 }\)
∴ 42.8 ÷ 0.25 = \(\frac { 428 }{ 100 }\) ÷ \(\frac { 2 }{ 100 }\)
= \(\frac { 428 }{ 10 }\) x \(\frac { 100 }{ 2 }\)
= \(\frac { 4280 }{ 25 }\)
= 2140
∴ \(\frac { 42.8 }{ 0.02 }\) = 2140
(iii) \(\frac { 5.6 }{ 1.4 }\)
since, 5.6 = \(\frac { 56 }{ 10 }\) and 1.4 = \(\frac { 14 }{ 100 }\)s
∴ 5.6 ÷ 1.4 = \(\frac { 56 }{ 10 }\) ÷ \(\frac { 14 }{ 10 }\)
= \(\frac { 56 }{ 10 }\) x \(\frac { 10 }{ 14 }\)
= \(\frac { 56 }{ 14 }\)
= 4
∴ \(\frac { 5.6 }{ 1.4 }\) = 4