GSEB Solutions Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3

Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 6 The Triangles and Its Properties Ex 6.3

Question 1.
Find the value of the unknown x in the following diagrams.

Solution:
(i) Using the angle sum property of a ‘triangle’ we have
50° + 60° + x = 180°
or 110° + x = 180°
or x = 180° – 110° = 70°
Thus, the required value of x is 70°.

(ii) Using the ‘angle sum property of a triangle’,
we have
30° + 90° + x = 180°
[the ∆ is right angled at P.]
or 120° + x = 180°
or x = 180° – 120° = 60°
Thus, the required value of x is 60°.

(iii) Using the ‘angle sum property of a triangle’, we have
30° + 110° + x = 180°
or 140° + x = 180°
or x = 180° – 140° = 40°
Thus, the required value of x is 40°.

(iv) Using the ‘angle sum property of a triangle’,
we have
x + x + 50° = 180°
∴ 2x + 50° = 180°
or 2x = 180° – 50° = 130°
or \(\frac { 2x }{ 2 }\) = \(\frac { 130° }{ 2 }\)
or x = 65°

(v) Using the ‘angle sum property of a triangle’, we have
x + x + x = 180°
or 3x = 180°
or \(\frac { 3x }{ 3 }\) = \(\frac { 180° }{ 3 }\)
or x = 60°

(vi) Using the ‘angle sum property of a triangle’, we have
x + 2x + 90° =180°
or 3x + 90° = 180°
or 3x = 180° – 90° = 90°
or \(\frac { 3x }{ 3 }\) = \(\frac { 90° }{ 3 }\)
[Dividing both sides by 3]
or x = 30°

Question 2.
Find the values of the unknown x and y in the following diagrams:

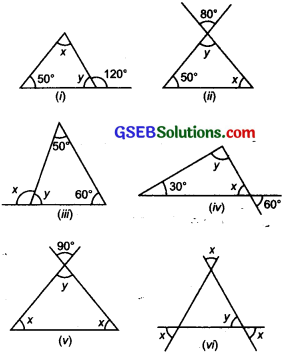
Solution:
(i) ∵ Angles y and 120° form a linear pair.
∴ y + 120° = 180°
or y = 180° – 120° = 60°
Now, using the angle sum property of a triangle, we have
x + y + 50° = 180°
or x + 60° + 50° = 180°
or x + 110° =180°
or x = 180° – 110° = 70°
Thus, \(\left.\begin{array}{l}
x=70^{\circ} \\
y=60^{\circ}
\end{array}\right\}\)

(ii) ∵ y and 80° angle are vertically opposite angles, then y = 80°
Now x + y + 50° = 180°
[Using angle sum property]
or x + 80° + 50° = 180°
or x + 130° = 180°
or x = 180° – 130° = 50°
Thus, \(\left.\begin{array}{l}
x=50^{\circ} \\
y=80^{\circ}
\end{array}\right\}\)

(iii) Using the angle sum property of triangle, we have
50° + 60° + y = 180°
or y + 110° = 180°
or y = 180° – 110° = 70°
Again, x and y form a linear pair.
∴ x + y = 180°
or x + 70° = 180°
or x = 180° – 70° = 110°
Thus, \(\left.\begin{array}{l}
x=110^{\circ} \\
y=70^{\circ}
\end{array}\right\}\)

(iv) ∵ x and 60° angle are vertically opposite angles
∴ x = 60°
Now, using the angle sum property of triangle, we have
x + y + 30° = 180°
or 60 + y + 30° = 180°
or y + 90° = 180°
or y = 180° – 90° =
Thus, \(\left.\begin{array}{l}
x=60^{\circ} \\
y=90^{\circ}
\end{array}\right\}\)

(v) ∵ y and 90° are vertically opposite angles, then y = 90°
Now, using the angle sum property of triangles, we have
x + x + y = 180°
2x + y = 180°
or 2x + 90° = 180°
or 2x = 180° – 90° = 90°
or \(\frac { 2x }{ 2 }\) = \(\frac { 90° }{ 2 }\) or x = 45°
Thus, \(\left.\begin{array}{l}
x=45^{\circ} \\
y=90^{\circ}
\end{array}\right\}\)

(vi) One angle of the triangle = y
Each of the other two angles is equal to their vertically opposite angle x.
∴ Using the angle sum property
x + x + y = 180°
or 2x+ y = 180°
or 2x + x = 180°
[x = y vertically opposite angles]
or 3x = 180°
or \(\frac { 3x }{ 3 }\) = \(\frac { 180° }{ 3 }\)
∴ x = 60°
But y = x
∴ y = 60°
Thus, \(\left.\begin{array}{l}
x=60^{\circ} \\
y=60^{\circ}
\end{array}\right\}\)