GSEB Solutions Class 7 Maths Chapter 11 Perimeter and Area InText Questions

Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 11 Perimeter and Area InText Questions and Answers.

Gujarat Board Textbook Solutions Class 7 Maths Chapter 11 Perimeter and Area InText Questions

Try These (Page 205)

Question 1.
What would you need to find, area or perimeter, to answer the following?
1. How much space does a blackboard occupy?
2. What is the length of a wire required to fence a rectangular flower bed?
3. What distance would you cover by taking two rounds of a triangular park?
4. How much plastic sheet do you need to cover a rectangular swimming pool?
Solution:
1. Area
2. Perimeter
3. Perimeter
4. Area
Note:

• Each side of a regular polygon is of the same length and each angle is of the same measure.
• Perimeter of a regular polygon = Length of a side x Number of sides.
• Perimeter of a square = 4 x Side.
• Area of a square = Side x Side.
• Perimeter of a rectangle = 2 x [Length + Breadth]
• Area of a rectangle = Length x Breadth.

Try These (Page 206)

Question 1.
Experiment with several such shapes and cut-outs. You might find it useful to draw these shapes on squared sheets and compute their areas and perimeters. You have seen that increase in perimeter does not mean that area will also increase.
Solution:
Please do this question yourself with the help of your subject teacher.

Question 2.
Give two examples where the area increases as the perimeter increases.
Solution:
Please do this question yourself with the help of your subject teacher.

Question 3.
Give two examples where the area does not increase when perimeter increases.
Solution:
Please do this question yourself with the help of your subject teacher.

Try These (Page 210)

Question 1.
Each of the following rectangles of length 6 cm and breadth 4 cm is composed of congruent polygons. Find the area of each polygon.

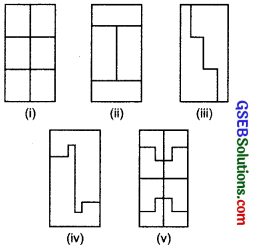
Solution:
∵ Length of the rectangle (l) = 6 cm
Breadth of the rectangle (b) = 4 cm
∴ Area of the rectangle = (l x b) = 6 x 4 cm² = 24 cm²

(i) Here, number of congruent polygons = 6
∴ Area of each polygon = \(\frac { 24 }{ 6 }\)cm²

(ii) Here, number of congruent polygons = 4
∴ Area of each polygon = \(\frac { 24 }{ 4 }\)cm² = 6 cm²

(iii) Here, number of congruent polygons = 2
∴ Area of each polygon = \(\frac { 24 }{ 2 }\) cm² = 12 cm²

(iv) Number of congruent polygons = 2
∴ Area of each polygon = \(\frac { 24 }{ 2 }\)cm² = 12 cm²

(v) Number of congruent polygons = 8
∴ Area of each polygon = \(\frac { 24 }{ 8 }\)cm² = 3 cm²

Try These (Page 212)

Question 1.
Find the area of the following parallelograms:

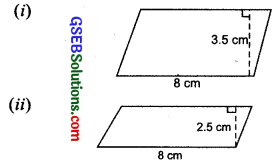
(iii) In a parallelogram ABCD, AB = 7.2 cm and the perpendicular from C on AB is 4.5 cm.
Solution:
(i) Base = 8 cm, Height = 3.5 cm
∴ Area of the parallelogram = Base x Height = 8 cm x 3.5 cm = 28 cm²

(ii) Base = 8 cm, Height = 2.5 cm
∴ Area of the parallelogram = Base x Height = 8 cm x 2.5 cm = 20 cm²

(iii) Base of parallelogram ABCD = (AB) = 7.2 cm
Height of parallelogram ABCD = 4.5 cm
∴ Area of parallelogram ABCD = Base x Height

Try These (Page 213)

Question 1.
Try the activity given on page 213, NCERT Textbook with different types of triangles.
Solution:
Do it yourself.

Question 2.
Take different parallelograms. Divide each of the parallelograms into two triangles by cutting any of its diagonals. Are the triangles congruents.
Solution:
Do it yourself.

Try These (Page 219)

Question 1.
In the adjoining figure,
(a) Which square has the larger perimeter?
(b) Which is larger, perimeter of smaller square or the circumference of the circle?

Solution:
(a) The outer square has the larger perimeter.
(b) The circumference of the circle is larger than the perimeter of the smaller square.

Try These (Page 222)

Question 1.
Draw circles of different radii on a graph paper. Find the drea by counting the number of squares. Also find the area by using the formula. Compare the two answers.
Solution:
Do it yourself.

Try These (Page 225)

Question 1.
Convert the following:
(i) 50 cm² in mm²
(ii) 2 ha in m²
(iii) 10 m² in cm²
Solution:
(i) 50 cm² in mm²
∵ 1 cm² = 100 mm²
∴ 50 cm² = 50 x 100 mm² = 5000 mm²

(ii) 2 ha in m²
∵ 1 ha = 10000 m²
∴ 2 ha = 2 x 10000 m² = 20000 m²

(iii) 10 m² in cm²
∵ 1 m² = 10000 cm²
∴ 10 m² = 10 x 10000 cm² = 100000 cm²

(iv) 1000 cm² in m²
∵ 10000 cm² = 1 m²
∴ 1 cm² = \(\frac { 1 }{ 10000 }\)m²
So, 1000 cm² = \(\frac { 1 }{ 10000 }\) x 100 m² = \(\frac { 1 }{ 10 }\)m² = 0.1 m²