Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 8 Comparing Quantities Ex 8.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 8 Comparing Quantities Ex 8.2
![]()
Question 1.
Convert the given fractional numbers to per cents.
(a) \(\frac { 1 }{ 8 }\)
(b) \(\frac { 5 }{ 4 }\)
(c) \(\frac { 3 }{ 40 }\)
(d) \(\frac { 2 }{ 7 }\)
Solution:
(a) We have \(\frac { 1 }{ 8 }\) = \(\frac { 1 }{ 8 }\) x \(\frac { 100 }{ 100 }\)
= \(\frac { 100 }{ 8 }\)%
= \(\frac { 1 }{ 8 }\)% or 12.5%
= \(\frac { 1 }{ 8 }\) = \(\frac { 25 }{ 2 }\)% or 12.5%
(b) We have \(\frac { 5 }{ 4 }\) = \(\frac { 5 }{ 4 }\) x \(\frac { 100 }{ 100 }\)
= \(\frac { 5×100 }{ 4 }\)%
= (5 × 25)% = 125%
Thus, = \(\frac { 5 }{ 4 }\) = 12.5%
(c) We have \(\frac { 3 }{ 40 }\) = \(\frac { 3 }{ 40 }\) x \(\frac { 100 }{ 100 }\)
= \(\frac { 3×100 }{ 40 }\)%
= \(\frac { 3×25 }{ 10 }\)%
= \(\frac { 75 }{ 10 }\)%
or 7.5%
Thus, \(\frac { 2 }{ 7 }\) = 28\(\frac { 4 }{ 7 }\)%
(d) We have \(\frac { 2 }{ 7 }\) = \(\frac { 2 }{ 7 }\) x \(\frac { 100 }{ 100 }\)
= \(\frac { 200 }{ 7 }\)%
= 28\(\frac { 4 }{ 7 }\)%
Thus, \(\frac { 2 }{ 7 }\) = 28\(\frac { 4 }{ 7 }\)%
![]()
Question 2.
Convert the given decimal fractions to percents.
(a) 0.65
(b) 2.1
(c) 0.02
(d) 12.35
Solution:

Question 3.
Estimate what part of the figures is coloured and hence find the per cent which is coloured.
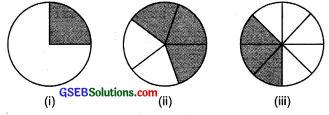
Solution:
(i) ∵ \(\frac { 1 }{ 4 }\) Part is shaded.
and \(\frac { 1 }{ 4 }\) = \(\frac { 1 }{ 4 }\) = \(\frac { 100 }{ 4 }\) = 25%
Thus, coloured part is 25%.
(ii) ∵ 3 parts out of 5 parts are shaded.
∴ \(\frac { 3 }{ 5 }\) part is shaded
and \(\frac { 3 }{ 5 }\) x 100% = 3 x 20% = 60%
Thus, 60% part is shaded
(iii) Here, 3 parts out of 8 parts are shaded.
∴ \(\frac { 3 }{ 5 }\) part is shaded
and \(\frac { 3 }{ 8 }\) x 100% = \(\frac { 3 }{ 2 }\) x 25% = \(\frac { 75 }{ 2 }\)% = 37.5%
Thus, 37.5% part is shaded.
![]()
Question 4.
Find:
(a) 15% of 250
(b) 1% of 1 hour
(c) 20% of ₹ 2500
(d) 75% of 1 kg
Solution:
(a) 15% of 250 = \(\frac { 15 }{ 100 }\) of 250
= \(\frac { 15×250 }{ 100 }\) = \(\frac { 75 }{ 2 }\)
= 37.5
(b) 1% of 1 hour = \(\frac { 100 }{ 60 }\) x 60 minutes
(∵ 1 hour = 60 minutes)
= \(\frac { 3 }{ 5 }\) minutes = \(\frac { 3 }{ 5 }\) x 60 seconds
= 36 seconds
Thus, 1% of 1 hour = 36 seconds
(c) 20% of ₹ 2500 = \(\frac { 20 }{ 100 }\) of 2500
= \(\frac { 20×2500 }{ 100 }\)
= 20 x 25 = 500
Thus, 20% of ₹ 2500 = ₹ 500
(d) 75% of 1 kg = 75% of 1000 g
(∵ 1 kg = 100g)
= \(\frac { 75}{ 100 }\) x 1000g
= \(\frac { 75×1000 }{ 100 }\)
= 750 g
Thus, 75% of 1 kg = 750 g
Question 5.
Find the whole quantity if
(a) 5% of it is 600.
(b) 12% of it is ₹ 1080.
(c) 40% of it is 500 km.
(d) 70% of it is 14 minutes.
(e) 8% of it is 40 litres.
Solution:
(a) 5% of a quantity is 600.
Let the quantity be x.
∴ 5% of x = 600
\(\frac { 5 }{ 100 }\) × x = 600 ⇒ x = \(\frac { 600×100 }{ 5 }\)
or x = 120 x 100 = 12000 .
Thus, the required quantity is 12000.
(b) 12% of a quantity is ₹ 1080.
Suppose the required quantity = x
∴ 12% of x = ₹ 1080
or \(\frac { 12 }{ 100 }\) × x = ₹ 1080 100
or x = ₹ \(\frac { 1080×100 }{ 12 }\)
= ₹ 9000
Thus, the required amount = ₹ 9000.
(c) 40% of a quantity is 500 km.
Let the quantity be x.
∴ 40% of x = 500 km
or \(\frac { 40 }{ 100 }\) × x = 500 km
or x = \(\frac { 500×100 }{ 40 }\) = 125 x 10 km
or x = 1250 km
Thus, the required quantity = 1250 km.
(d) 70% of a quantity is 14 minutes.
Let the required quantity be x.
∴ 70% of x = 14 minutes
or \(\frac { 70 }{ 100 }\) × x = 14 minutes
or x = \(\frac { 14×100 }{ 70 }\)
= 20 minutes
Thus, the required quantity = 20 minutes.
(e) 8% of a quantity is 40 litres.
Let the quantity be x.
∴ 8% of x = 40 litres
or x = \(\frac { 40×100 }{ 8 }\)
x = 500 litres.
Thus, the required quantity is 500 litres.
![]()
Question 6.
Convert given per cents to decimal fractions and also to fractions in simplest forms:
(a) 25%
(b) 150%
(c) 20%
(d) 5%
Solution:
(a) We have 25% = \(\frac { 25 }{ 100 }\) = \(\frac { 1 }{ 4 }\)
Thus, 25% = \(\frac { 1 }{ 4 }\)
(b) We have 150% = \(\frac { 150 }{ 100 }\) = \(\frac { 3 }{ 2 }\)
Thus, 150% = \(\frac { 3 }{ 2 }\)
(c) We have 20% = \(\frac { 20 }{ 100 }\) = \(\frac { 1 }{ 5 }\)
Thus, 20% = \(\frac { 1 }{ 5 }\)
(d) We have 5% = \(\frac { 5 }{ 100 }\) = \(\frac { 1 }{ 20 }\)
Thus, 5% = \(\frac { 1 }{ 20 }\)
Question 7.
In a city, 30% are females, 40% are males and remaining are children. What per cent are children?
Solution:
∵ Females are 30% and males are 40%.
∴ Remaining part of the population
= 100% – (30 + 40)%
= 100% – 70% = 30%
Thus, children are 30% of the population.
Question 8.
Out of 15,000 voters in a constituency, 60% voted. Find the percentage of voters who did not vote. Can you now find how many actually did not vote?
Solution:
Total voters = 15000
Part of voters who voted = 60%
∴ Part of voters who did not vote
= 100% – 60%
= (100 – 60)% = 40%
Now, 40% of 15000 = \(\frac { 40 }{ 100 }\) x 15000
= 40 x 150 = 6000
Thus, 6000 voters did not vote.
![]()
Question 9.
Meeta saves ₹ 400 from her salary. If this is 10% of her salary, what is her salary?
Solution:
Saving = 10% of the salary
Consider the salary = ₹ x
Saving = 10% of x
So, we have 10% of x = ₹ 400 10
Thus, the salary = ₹ 4000.
Question 10.
A local cricket team played 20 matches in one season. It won 25% of them. How many matches did they win?
Solution:
Total number of matches played = 20
Part of matches won = 25%
∵ 25% of 20 = \(\frac { 25 }{ 100 }\) x 20 = 5 100
∴ The team won 5 matches.
![]()