Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1
Question 1.
Evaluate:
(i) 3-2
(ii) (-4)-2
(iii) (\(\frac{1}{2}\))-5
Solution:
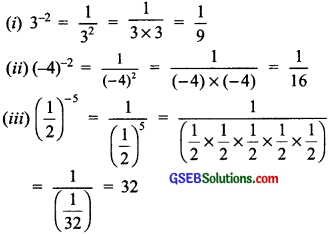
![]()
Question 2.
Simplify and express the result in power notation with positive exponent?
(i) (-4)5 + (-4)8
(ii) \(\left(\frac{1}{2^{3}}\right)^{2}\)
(iii) (-3)4 × (\(\frac{5}{3}\))4
(iv) (3-7 + 3-10) × 3-5
(v) 2-3 × (-7)-3
Solution:
(i) (-4)5 + (-4)8
∵ am + an = am-n
∴ (-4)5 + (-4)8 = (-4)5-8
= (-4)-3 = \(\frac{1}{(-4)^{3}}\)
(ii)

(iii)
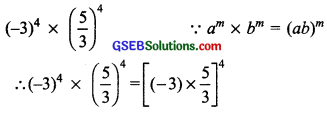
= [(-1) × 5]4 = [(-1)4 × (+5)4]
= 1 × (5)4 = (5)4
(iv) (3-7 ÷ 3-10) × 3-5
∵ am + an = am-n and am × an = am+n
∴ (3-7 ÷ 3-10 × 3-5 = [3-7-(-10)] × 3-5
= 33+(-5) = 3-2 = \(\frac{1}{(3)^{2}}\)
(v) 2-3 × (-7)-3
∵ am × bm = (ab)m
∴ 2-3 × (-7)-3 = [2 × (-7)]-3
= [-14]-3 = \(\frac{1}{(-14)^{3}}\)
![]()
Question 3.
Find the value of:
(i) (30 + 4-1) × 22
(ii) (2-1 × 4-1) + 2-2
(iii) (\(\frac{1}{2}\))-2 + (\(\frac{1}{3}\))-2 + (\(\frac{1}{4}\))-2
(iv) (3-1 + 4-1 + 5-1)0
(v) {(\(\frac{-2}{3}\))-2}2
Solution:
(i) (30 + 4-1) × 22
∵ a0 = 1 and a-1 = \(\frac{1}{a}\)
∴ (30 + 4-1) × 22
= (1 + \(\frac{1}{2}\)) 22 = \(\frac{5}{4}\) × 4 = 5
(ii) (2-1 × 4-1) ÷ 2-2
∵ am × bm = (ab)m
∴ (2-1 × 4-1) + 2-2 = (2 × 4-1) ÷ 2-2
= (21 × 22)-1 ÷ 2-2
= (21+2)-1) ÷ 2-2 = (23)-1 ÷ 2-2
= 2-3 ÷ 2-2 = (2)(-3)-(-2)
= (-2)-3+2 = 2-1 = \(\frac{1}{2}\)
(iii)
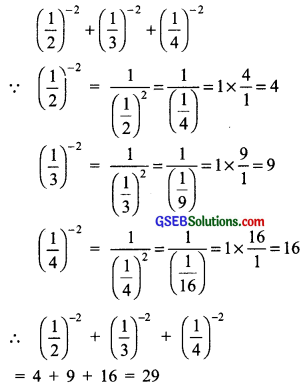
(iv)
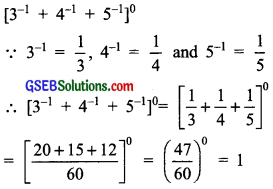
(v)

Question 4.
Evaluate
- \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\) and
- (5-1 × 2-1) × 6-1
Solution:
1. \(\frac{8^{-1} \times 5^{3}}{2^{-4}}\) = \(\frac{8^{-1} \times(5 \times 5 \times 5)}{2^{-4}}\)
= \(\frac{1}{8}\) × 24 × 125 = \(\frac{1}{8}\) × 2 × 2 × 2 × 2 × 125
= 2 × 125 = 250
2. (5-1 × 2-1) × 6-1) = (5 × 2-1) × 6-1)
= 10-1 × 6-1
= (10 × 6-1) = 60-1 = \(\frac{1}{60}\)
![]()
Question 5.
Find the value of m for which 5m + 5-3 = 55.
Solution:
∵ am × bm = (ab)m
∴ L.H.S = 5m + 5-3
= 5m-(-3)
= 5m+3
Now, 5m+3 = 55
Since, bases 5 are equal, therefore exponents are also equal.
i.e; m + 3 = 5
or m = 5 – 3 = 2
Thus, the required value of m is 2.
Question 6.
Evaluate:
(i) \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
(ii) \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}\)
Solution:

![]()
Question 7.
Simplify:
(i) \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\) (t ≠ 0)
(ii) \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
Solution:
