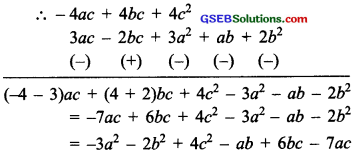Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3
Question 1.
Complete the table.

Solution:
We have:
1. a × (b + c + d) = a × b + a × c + a × d
= ab + ac + ad
2. (x + y – 5) × 5xy
= x × 5xy + y × 5xy + (-5) × 5xy
= 5x2y + 5x2y – 25xy
3. p × (6p2 – 7p + 5)
= p × 6p2 + p × (-7p) + p × 5
= 6p3 – 7p2 + 5p
4. 4p2q2 × (p2 – q2)
= 4p2q2 × p2 + 4p2q2 × (-q2)
= (4 × 1) × p2q2 × p2 + [4 x (-1)] × p2q2 × (-q2)
= 4 × p4q2 + (-4) × p2q4 = 4p4q2 – 4p2q4
5. (a + b + c) × abc
= a × abc + b × abc + c × abc
= (1 × 1) × a × abc + (1 × 1) × b × abc + (1 × 1) × c × abc
= (1) × a2bc + (1) × ab2c + abc2
![]()
Question 2.
Find the product?
- (a2) × (2a22) × (4a26)
- (\(\frac{2}{3}\)xy) × (\(\frac{-9}{10}\)x2y2)
- (-\(\frac{10}{3}\)pq3) × (\(\frac{6}{5}\)p3q)
- x × x2 × x4 × x4
Solution:
1. (a2) × (2a22) × (4a26)
= (1 × 2 × 4) × a2 × a22 × a26
= 8 × a50 [∵2 + 22 + 26 = 50]
= 8a50
2. (\(\frac{2}{3}\)xy) × (-\(\frac{9}{10}\)x2y2) = \(\frac{2}{3}\) × (-\(\frac{9}{10}\)) × xy × x2y2
= – \(\frac{2}{3}\) × \(\frac{9}{10}\) × x3y3 = \(\frac{-3}{5}\)x3y3
3. (-\(\frac{10}{3}\)pq3) × p3q
= [(-\(\frac{10}{3}\)) × \(\frac{6}{5}\)] × pq3 × p3q
= –\(\frac{10}{3}\) × \(\frac{6}{5}\) × p4q4 = -4p4q4
4. x × x2 × x3 × x4
= (1 × 1 × 1 × 1) × x × x2 × x3 × x4
= (1) × x10 = x10
![]()
Question 3.
(a) Simplify 3x(4x – 5) + 3 and find its values for
(i) x = 3 and
(ii) x = \(\frac{1}{2}\).
(b) Simplify a(a2 + a + 1) + 5 and find its value for
(i) a = 0
(ii) a = 1 and
(iii) a = -1.
Solution:
(a) 3x(4x – 5) + 3 = 3x × 4x + 3x × (-5) + 3
= (3 × 4) × x × x + 3 × (-5) × x + 3
= 12 × x2 + (-15) × x + 3
= 12x2 – 15x + 3
(i) For x = 3, 12x2 – 15x + 3
= 12(3)2 – 15(3) + 3
= 12 × 9 – 45 + 3
= 108 + 3 – 45
= 111 – 45 = 66
(ii) For x = \(\frac{1}{2}\), 12x2 – 15x + 3
= 12(\(\frac{1}{2}\))2 – 15(\(\frac{1}{2}\)) + 3
= 12(\(\frac{1}{4}\)) – \(\frac{15}{2}\) + 3 = 3 – \(\frac{15}{2}\) + 3 = 6 – \(\frac{15}{2}\)
= \(\frac{12-15}{2}\) = \(\frac{-3}{2}\)
(b) a(a2 + a + 1) + 5
= a × a2 + a × a + a × 1 + 5
= a3 + a2 + a + 5
(i) For a = 0, a3 + a2 + a + 5
= (1)3 + (1)2 + (1) + 5
= 1 + 1 + 1 + 5 = 8
(ii) For a = 1, a3 + a2 + a + 5
= (1)3 + (1)2 + (1) + 5
= 1 + 1 + 1 + 5 = 8
(iii) For a = -1, a3 + a2 + a + 5
= (-1)3 + (-1)2 + (-1) + 5
= -1 + 1 – 1 + 5 = 4
![]()
Question 4.
(a) Add: p(p-q), q(q-r) and r(r-p)
(b) Add: 2x(z – x – y) and 2y(z – y – x)
(c) Subtract: 3l (l – 4m + 5n) from 4l (10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(-a + b + c)
Solution:
(a) ∵ p(p -q) = p × p – p × q = p2 – pq
q(q – r) = q × q – q × r = q2 – qr
and r(r – p) = r × r – r × p = r2 – rp
∴ Adding the above products, we have
(p2 – pq) + (q2 – qr) + (r2 – rp)
= p2 – pq + q2 – qr + r2 – rp
= p2 + q2 + r2 – pq – qr – rp
= p2 + q2 + r2 – (pq + qr + rp)
(b) ∵ 2x(z – x – y) = 2x × z – 2x × x – 2x × y
= 2xz – 2x2 – 2xy and 2y(z – y – x)
= 2y × z – 2y × y – 2y × x
= 2yz – 2y2 – 2yx
(c) ∵ 3l(l – 4m + 5n)
= 3l × l – 3l × 4m + 3l × 5n
= 3l2 – 12lm + 15ln and 4l(10n – 3m + 2l)
= 4l × 10n – 4l × 3m + 4l × 2l
= 40ln – 12lm + 8l2
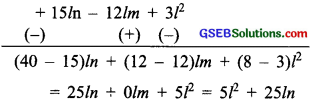
(d) ∵ 3a(a + b + c) – 2b(a – b + c)
= [3a × a + 3a × b + 3a × b + 3a × c] – 2b(a × a + 2b × (-b) + 2b × c]
= [3a2 + 3ab + 3ac] – [2ab – 2b2 + 2abc]
= 3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc
= 3a2 + ab + 3ac + 2b2 – 2bc and 4c(-a + b + c)
= 4c × (-a) + 4c × b + 4c × c
= – 4ac + 4bc + 4c2