Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 3 Understanding Quadrilaterals InText Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths 3 Understanding Quadrilaterals InText Questions
Try These (Page 43)
Question 1 .
Take a regular hexagon as shown in the figure:
1. What is the sum of the measures of its exterior angles x, y, z, p, q, r?
2. Is x = y = z = p = q = r? Why?
3. What is the measure of each?

(i) exterior angle
(ii) interior angle
4. Repeat this activity for the cases of
(i) A regular octagon
(ii) a regular 20-gon
Solution:
1. ∠x + ∠y + ∠z + ∠p + ∠q + ∠r = 360°
[∵ Sum of exterior angles of a polygon = 360°]
2. Since, all the sides of the polygon are equal.
∴ It is a regular hexagon.
So, its interior angles are equal.
x = (180° – a) y = (180° – a)
z = (180° – a) p = (180° – a)
q = (180° – a) r = (180° – a)
∴ x – y = z = p = q = r
3.
(i) ∵ x + y + z + p + q + r = 360°
[∵ sum of exterior angles = 360°] and all these angles are equal.
∴ Measure of each exterior angle
= \(\frac{360^{\circ}}{6}\) = 60°
(ii) ∵ Exterior angle = 60°
∴ 180° – 60° = Interior angle
or 120°= Interior angle
or Measure of interior angle = 120°
4.
(i) In a regular octagon, number of sides (n) = 8
∴Each exterior angle = \(\frac{360^{\circ}}{8}\) = 45°
∴Each interior angle = 180° – 45° = 135°
(ii) For a regular 20-gon, the number of sides (n) = 20
∴Each exterior angle = \(\frac{360^{\circ}}{20}\) = 18°
Thus, each interior angle = 180° – 18° = 162°
![]()
Question 2.
Find the number of sides of a regular polygon whose each exterior angle has a measure of 40°?
Solution:
Since, the given polygon is a regular polygon.
∴ Its each exterior angle is equal.
∵ Sum of all the exterior angles = 360°
∴ Number of exterior angles = \(\frac{360^{\circ}}{40^{\circ}}\) = 9
⇒ Number of sides = 9
Thus, it is a nonagon.
Try These (Page 47)
Question 1.
Take two identical set squares with angles 30° – 60° – 90° and place them adjacently to form a parallelogram as shown in Figure? Does this help to you to verify the above property?
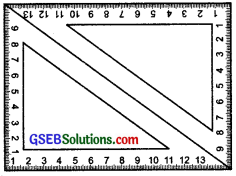
Solution:
The given figure helps us to verify that Opposite sides of a parallelogram are of equal length.
Try These (Page 48)
Question 1.
Take two identical 30° – 60° – 90° set – squares and form a parallelogram as before. Does the figure obtained help you to confirm the above property?
Solution:
Above figure also help us to confirm that: opposite angles of a parallelogram are equal.
Try These (Page 50)
Question 1.
After showing m∠R = m∠N = 70°, can you find m∠I and m∠G by any other method?

Solution:
Yes, without using the property of a parallelogram, we can also find m∠I and m∠G as given below:
∵ m∠R = m∠N = 70° and RG || IN. the transversal RI intersecting them.
∴ m∠R + m∠I = 180°
[Sum of interior opposite angles is 180°]
or 70° + m∠I = 180°
m∠I = 180° – 70° = 110°
Similarly, m∠G = 110°
![]()
Question 2.
In the figure. ABCD is a parallelogram. Given that OD = 5 cm and AC is 2 cm less than BD. Find OA?
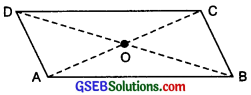
Solution:
∵ Diagonals of a parallelogram bisect each other.
∴ OD = OB =5 cm
or OB = 5cm
or BD = 5 cm × 2 = 10 cm
∵ AC = BD – 2cm
∴ AC = (10 – 2) cm = 8 cm
0r \(\frac{1}{2}\) AC = \(\frac{1}{2}\) × 8 cm = 4cm
or OA = 4 cm.
Try These (Page 56)
Question 1.
A mason has made a concrete slab. He needs it to be rectangular In what different ways can he make sure thai it is rectangular?
Solution:
He can make sure thai it is rectangular using the following different ways:
- By making opposite sides of equal length.
- By keeping each angle at the corners as 900.
- By keeping the diagonals of equal length.
- By making opposite sides parallel and ensuring one angle as 900 in measure.
- By making all angles equal and ensuring the measure of one angle as 900.
![]()
Question 2.
A square was defined as a rectangle with all sides equal. Can we dfine it as rhombus with equal angles? Explore this idea?
Solution:
Yes, because a rhombus becomes a square if its all angles are equal.
Question 3.
Can a trapezium have all angles equal? Can it have all sides equal? Explain?
Solution:
Yes, if it is a rectangle. It can have all sides equal, when it becomes a square.