Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 7 Cube and Cube Roots Ex 7.1
Question 1.
Which of the following numbers are not perfect cubes?
- 216
- 128
- 1000
- 100
- 46656
Solution:
1. We have
216 = 2 × 2 × 2 × 3 × 3 × 3
Grouping the prime factors of 216 into triples, no factor is left over.
∴ 216 is a perfect cube.

2. We have
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
Grouping the prime factors of 128 into triples, we are left over with 2 as ungrouped factor.
∴ 128 is not a perfect cube.
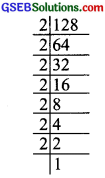
3. We have 211000
1000 = 2 × 2 × 2 × 5 × 5 × 5
Grouping the prime factors of 1000 into triples, we are not left over with any factor.
∴ 1000 is a perfect cube.
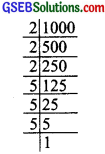
4. We have
100 = 2 × 2 × 5 × 5
Grouping the prime factors into triples, we do not get any triples.
Factors 2 × 2 and 5 × 5 are not in triples.
∴ 100 is not a perfect cube.

5. We have
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3

Grouping the prime factors of 46656 in triples we are not left over with any prime factor.
∴ 46656 is a perfect cube.
![]()
Question 2.
Find the smallest number by which each of the following numbers must obtain a perfect cube?
- 243
- 256
- 72
- 675
- 100
Solution:
1. We have
243 = 3 × 3 × 3 × 3 × 3
The prime factor 3 is not a group of three.
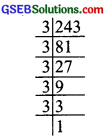
∴ 243 is not a perfect cube.
Now, [243] × 3 = [3 × 3 × 3 × 3 × 3] × 3
or 729 = 3 × 3 × 3 × 3 × 3 × 3 × 3
Now, 729 becomes a perfect cube.
Thus, the smallest required number to multiply 243 to make it a perfect cube is 3.
2. We have
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
Grouping the prime factors of 256 in triples, we are left over with 2 × 2.
∴ 256 is not a perfect cube.

Now, [256] × 2
= [2 × 2 × 2 × 2 × 2 × 2 × 2 × 2] × 2
or 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
i.e; 512 is a perfect cube.
Thus, the required smallest number is 2.
3. We have 72 = 2 × 2 × 2 × 3 × 3
Grouping the prime factors of 72 in triples, we are left over with 3 × 3.
∴ 72 is not a perfect cube.
Now, [72] × 3
= [2 × 2 × 2 × 3 × 3] × 3
or 216 = 2 × 2 × 2 × 3 × 3 × 3
i.e; 216 is a perfect cube.
∴ The smallest number required to multiply 72 to make it a perfect cube is 3.

4. We have 675 = 3 × 3 × 3 × 5 × 5
Grouping the prime factors of 675 to triples, we are left over with 5 × 5.
∴ 675 is not a perfect cube.
Now, [675] × 5
= [3 × 3 × 3 × 5 × 5] × 5
or 3375 = 3 × 3 × 3 × 5 × 5 × 5
Now, 3375 is a perfect cube.
Thus, the smallest required number to multiply 675 such that the new number is a perfect cube is 5.

5. We have
100 = 2 × 2 × 5 × 5

The prime factor are not in the groups of triples.
∴ 100 is not a perfect cube.
Now, [100] × 2 × 5 = [2 × 2 × 5 × 5] × 2 × 5
or [100] × 10 = 2 × 2 × 2 × 5 × 5 × 5
1000 = 2 × 2 × 2 × 5 × 5 × 5
Now, 1000 is a perfect cube.
Thus, the required smallest number is 10.
![]()
Question 3.
Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.
- 81
- 128
- 135
- 192
- 704
Solution:
1. We have 81 = 3 × 3 × 3 × 3

Grouping the prime factors of 81 into triples, we are left with 3
∴ 81 is not a perfect cube.
Now, [81] + 3 [3 × 3 × 3 × 3] ÷ 3
or 27 – 3 × 3 × 3
i.e., 27 is a prefect cube.
Thus, the required smallest number is 3.
2. We have 2 128
128 = 2 × 2 × 2 × 2 × 2 × 2 × 2
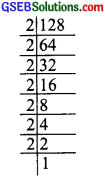
Grouping the prime factors of 128 into triples, we are left with 2.
∴ 128 is not a perfect cube
Now, [128] ÷ 2
= [2 × 2 × 2 × 2 × 2 × 2 × 2] + 2
or 64 = 2 × 2 × 2 × 2 × 2 × 2
i.e.. 64 is a perfect cube.
Thus, the required smallest number is 2.
3. We have 135 = 3 × 3 × 3 × 5

Grouping the prime factors of 135 into triples, we are left over with 5.
135 is not a perfect cube.
Now, [135] + 5 = [3 × 3 × 3 × 5] + 5
or 27 = 3 × 3 × 3
i.e., 27 is a perfect cube.
Thus, the required smallest number is 5.
4. We have
192 = 2 × 2 × 2 × 2 × 2 × 2 × 3

Grouping the prime factors of 192 into triples, 3 is left over.
∴ 192 is not a perfect cube.
Now, [192] + 3
= [2 × 2 × 2 × 2 × 2 × 2 × 2 × 3] + 3
or 64 = 2 × 2 × 2 × 2 × 2 × 2
i.e., 64 is a perfect cube.
Thus, the required smallest number is 3.
5. We have
704 = 2 × 2 × 2 × 2 × 2 × 2 × 11

Grouping the prime factors of 704 into triples, 11 is left over.
∴ [704] + 11
= [2 × 2 × 2 × 2 × 2 × 2 × 11] ÷ 11
or 64 = 2 × 2 × 2 × 2 × 2 × 2
i.e; 64 is a perfect cube.
Thus, the required smallest number is 11.
![]()
Question 4.
Pariksht makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Solution:
Sides of the cuboid are: 5 cm, 2 cm, 5 cm
∴ Volume of the cuboid = 5 cm × 2cm × 5 cm
To form it as a cube its dimension should be in the group of triples.
∴ Volume of the required cube
= [5 cm × 5 cm × 2 cm] × 5 cm × 2 cm × 2 cm
= [5 × 5 × 2cm3] = 20cm3
Thus, the required number of cuboids = 20