Gujarat Board GSEB Solutions Class 9 Maths Chapter 10 Circles Ex 10.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 10 Circles Ex 10.3
Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
A pair of circles can be drawn in the following condition:
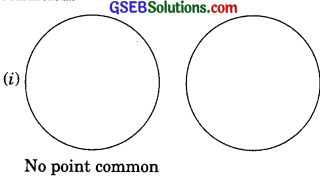
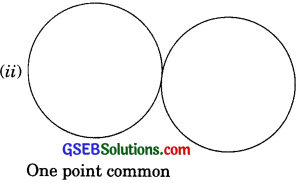
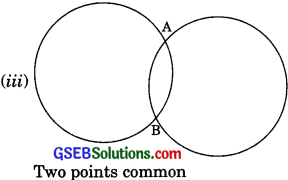
The maximum number of common points is two.
Question 2.
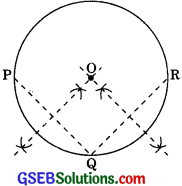
Suppose you are given a circle. Give the construction to find its centre.
Solution:
Steps of construction:
(i) Take any three points P, Q and R on the circle.
(ii) Join PQ and QR.
(iii) Draw the perpendicular bisectors of PQ and QR. Let these intersect at O. Then, O is the centre of the circle.
Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Solution:
Given: Two circles with centres O and P intersecting at A and B.
Prove: OP is the perpendicular bisector of AB.
Construction: Join OA, OB, PA and PB. Let OP intersect AB at M.
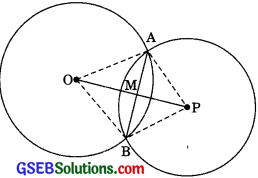
Proof: In ΔOAP and ΔOBP,
OA = OB [Radii of a circle]
PA = PB [Radii of a circle]
OP = OP [Common]
ΔOAP = ΔOBP [SSS Rule]
∴ ∠AOP = ∠BOP [CPCT]
= ∠AOM = ∠BOM ……….(1)
In ΔAOM and ΔBOM,
OA = OB [Radii of a circle]
∠AOM = ∠BOM (From (1))
OM = OM [Common]
∴ ΔAOM = ΔBOM [SAS Rule]
∴ AM = BM ……..(2) [CPCT]
and ∠AMO = ∠BMO ……..(3) ECPCTI
But ∠AMO + ∠BMO = 180° [Linear pair axiomi]
∠AMO = ∠BMO = 90° ……… (4)
∴ OM, i.e., OP is the perpendicular bisector of AB. [From (2) and (4)]
![]()