Gujarat Board GSEB Solutions Class 9 Maths Chapter 11 Constructions Ex 11.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 11 Constructions Ex 11.2
Question 1.
Construct a triangle ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Given: In ΔABC, BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Required: To construct the triangle ABC.
Steps of construction:
(1) Draw the base BC = 7 cm.
(2) At point B make an angle XBC = 75°.
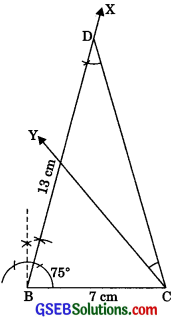
(3) Cut a line segment BD equal to AB + AC = 13 cm from the ray BX.
(4) Join DC.
(5) Make a ∠DCY = ∠BDC.
(6) Let CY intersect BX at A. Then, ABC is the required triangle.
![]()
Question 2.
Construct a triangle ABC in which BC = 8 cm ∠B = 45° and AB – AC = 3.5cm.
Solution:
Given: In ΔABC, BC = 8 cm, ∠B = 45° an AB – AC = 3.5cm.
Required: To construct the triangle ABC.
Steps of construction
(1) Draw the base BC = 8 cm.
(2) At point B, make an angle XBC = 45°.
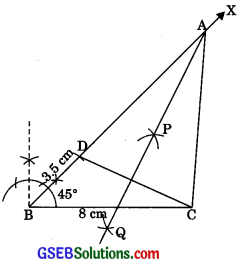
(3) Cut the line segment BD equal’ to AB – AC = 3.5 cm from the ray BX.
(4) Join DC.
(5) Draw the perpendicular bisector, say PQ of DC.
(6) Let it intersect BX at a point A.
(7) Join AC.
Then, ABC is the required triangle.
Question 3.
Construct a triangle PQR in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Given: In ∠PQR, QR = 6 cm, ∠Q = 60° and PR – PQ = 2cm.
Required: To construct the APQR.
Steps of construction:
(1) Draw the base QR = 6 cm.
(2) At the point Q makes an ∠XQR = 60°.
(3) Cut the line segment QS = PR – PQ (= 2 cm) from the line, QX extended on the opposite side of the line segment QR.
(4) Join SR.
(5) Draw the perpendicular bisector LM of SR.
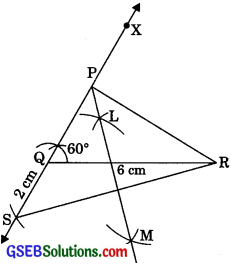
(6) Let LM intersect QX at P.
(7) Join PR.
Then, PQR is the required triangle.
![]()
Question 4.
Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11cm.
Solution:
Given: In triangle XYZ, ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Required: To construct the XYZ.
Steps of construction:
(1) Draw a line segment BC = XY + YZ + ZX = 11 cm.
(2) Make ∠LBC = ∠Y = 30° and ∠MCB = ∠Z = 90°
(3) Bisect ∠LBC and ∠MOB. Let these bisectors meet at a point X.
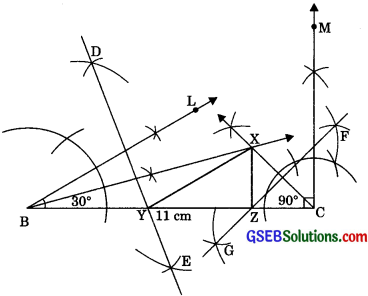
(4) Draw perpendicular bisectors DE of XB and FG of XC.
(5) Let DE intersect BC at Y and FG intersect BC at Z.
(6) Join XY and XZ. Then, XYZ is the required triangle.
![]()
Question 5.
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Given: In right ΔABC, base BC = 12 cm, ∠B = 90° and AB + AC = 18 cm.
Required: To construct the right triangle ABC.
Steps of construction:
(1) Draw the base BC = 12 cm.
(2) At point B, make an ∠XBC = 90°.
(3) Cut a line segment BD = AB + AC = 18 cm from the ray BX.
(4) Join DC.
(5) Draw the perpendicular bisector PQ of CD to intersect BD at a point A.
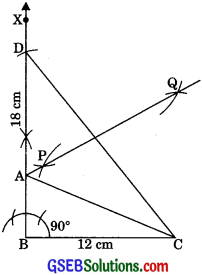
(6) Join AC.
Then, ABC is the required right triangle.