Gujarat Board GSEB Solutions Class 9 Maths Chapter 10 Circles Ex 10.4 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 10 Circles Ex 10.4
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Solution:
Let two circles with centres O and O’ intersect each other at P and Q.
Therefore, OP = OQ = 5cm, O’P = O’Q = 3cm and OO’ = 4 cm
In ΔOOP, OO’2 + OP2 = 42 + 32
= 16 + 9 = 25
= 52 = OP2
∴ AOO’P = 90° (Using converse of Pythagoras Theorem)
But OO’ ⊥ PQ
As if two circles intersect each other at two points, then the line joining their centres is the perpendicular bisector of their common chord.
∴ OO’ coincides 0M i.e., PQ passes through the centre O’.
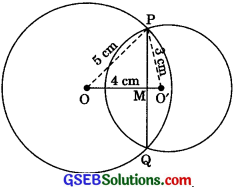
∴ Length of the common chord
PQ = 2O’P = 2 x 3 cm = 6 cm.
![]()
Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Solution:
Given: A circle with centre O. Its two equal
chords AB and CD intersect at E.
To Prove: AE = DE and CE = BE.
Construction: Draw OM ⊥ AB and ON ⊥ CD. Join OE.
Proof: In ΔOME and ΔONE,
OM = ON
[∴ Equal chords of a circle are equidistant from the centre.]
OE = OE [Common]
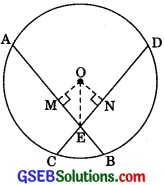
∴ ΔOME = ΔONE [RHSI
∴ ME = NE [CPCT]
⇒ AM + ME = DN + NE
|∴ AM = DN = \(\frac {1}{2}\) AB = \(\frac {1}{2}\) CD|
AE = DE
Now, AB – AE = CD – DE [Given AB = CD]
⇒ BE = CE
![]()
Question 3.
if two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Solution:
Given: Two equal chords AB and CD of a circle with centre O intersect within the circle. Their point of intersection is E.
To Prove: ∠OEA = ∠OED.
Construction: Join OA and OD
Proof: In ΔOEA and ΔOED,
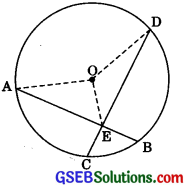
OE = OE [Common]
OA = OD [Radii of a circle]
AE = DE [Proved in 2 above]
∴ ΔOEA. = ΔOED [SSS Rule]
∴ ∠OEA = ∠OED [CPCT]
Note: Also it can be drawn OP⊥ AB, OQ ⊥ CD and shown ΔOPE = ΔOQE to prove ∠OEP = ∠OEQ.
![]()
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD [see figure].
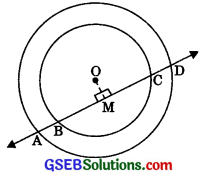
Solution:
Construction: Draw OM ⊥ BC.
Proof: The perpendicular drawn from the centre of a circle to a chord bisects the chord.
∴ AM = DM ……….(1)
and BM = CM ………..(2)
Subtracting (2) from (1), we get
AM – BM = DM – CM
∴ AB = CD.
![]()
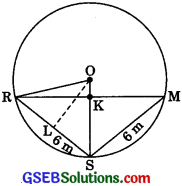
Question 5.
Three girls Reshma, Salina and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salina and between Salina and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Solution:
Let KR = xm
ar(ΔORS) = ar(ΔORK) + ar(ΔSRK)
= \(\frac {(0K) (KR)}{2}\) + \(\frac {(KS) (OS)}{2}\)(KS) (KR)
= \(\frac {(x) (5)}{2}\) ………..(1)
Again, ar(ΔORS)
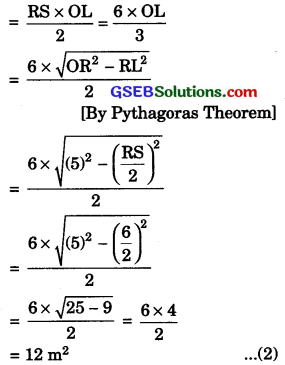
From equations (1) and (2),
\(\frac {(x) (5)}{2}\) = 12
⇒ x = \(\frac {12 x 2}{5}\) = \(\frac {24}{5}\) = 4.8 m
⇒ KR = 4.8m
RM = 2 KR = 2 x (4.8) = 9.6km
∴ Hence, the distance between Reshma and Mandip is 9.6m.
![]()
Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
Solution:
Let BD = xm
Then in right triangle ODB,
OB2 = OD2 + BD2 [By Pythagoras Theorem]
Take AB = BC = AC
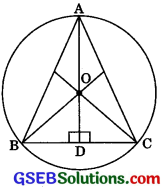
⇒ (20)2 = OD2 + x2
⇒ OD2 = 400 – x2
⇒ OD = \(\sqrt{400-x^{2}}\)
Area of equilateral ΔABC
ABC = \(\frac{\sqrt{3}}{4}\) (side)2 = \(\frac{\sqrt{3}}{4}\)BC2
= \(\frac{\sqrt{3}}{4}\) (2BD)2 = \({\sqrt{3}\)BD2 = \({\sqrt{3}\)x2 ………..(1)
Again, area of equilateral triangle ABC
= Area of ΔOBC + Area of ΔOCA + Area of ΔOAB
= 3 Area of ΔOBC = 3 \(\frac{(BC) (OD)}{2}\)
= \(\frac{3(2BD) (OD)}{2}\) = 3 (BD) IAD)
= 3 x \(\sqrt{400-x^{2}}\) ……….(2)
From equations (1) and (2),
3 x \(\sqrt{400-x^{2}}\) = \(\sqrt{3}\) x2 ………….(2)
⇒ \(\sqrt{3}\)\(\sqrt{400-x^{2}}\) = x
Squaring both sides,
3(400 – x2) = x2
⇒ 1200 – 3x2 = x2
⇒ 4 x 2 = 1200 ⇒ x2 = 300
⇒ x = 10\(\sqrt{3}\) ⇒ BD = 10\(\sqrt{3}\)
2BD = 20\(\sqrt{3}\) ⇒ BC = 20 \(\sqrt{3}\)
Hence, the length of string of each phone is 20\(\sqrt{3}\) m.
![]()
Alternative method: In an equilateral triangle length of altitude = \(\frac{\sqrt{3}}{4}\) (side)
AD = \(\frac{\sqrt{3}}{4}\) BC ………..(1)
Also, centroid of a triangle divides its median in the ratio 2: 1
∴ AO : OD = 2 : 1 or AO : AD = 2 : 3
AD = \(\frac{3}{4}\) AO ………..(2)
From (1) and (2), \(\frac{\sqrt{3}}{2}\)BC = \(\frac{3}{4}\) AO
⇒ BC = \(\sqrt{3}\) AO
= 20 \(\sqrt{3}\) m