Gujarat Board GSEB Solutions Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (See fig.) AC is a diagonal. Show that
1. SR || AC and SR = \(\frac {1}{2}\) AC
2. PQ = SR
3. PQRS is a parallelogram.
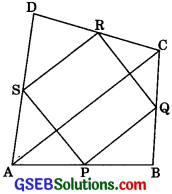
Solution:
1. In ΔADC,
S and R are mid-points of AD and DC.
∴ SR || AC and SR = \(\frac {1}{2}\) AC …….(1)
(Line segment joining the mid-points of two sides of a triangle is parallel and half of the third side.)
2. In ΔABC,
P and Q are mid-points of AB and BC respectively.
PQ || AC and PQ = \(\frac {1}{2}\) AC ……(2)
(A line segment joining the mid-points of two sides of a triangle is parallel and half of the third side)
From eqn. (1) and (2),
PQ = SR
3. From eqn. (1) and (2),
PQ II SR and PQ = SR
∴ PQRS is a parallelogram.
(If one pair of opposite sides of a quadrilateral is equal and parallel, then it is a parallelogram).
![]()
Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: ABCD is a rhombus, P, Q, R, S are mid-points of AB, BC, CD, DA respectively. PQ, QR, RS and SP are joined.
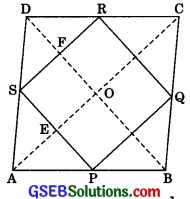
To Prove: PQRS is a rectangle.
Construction: Join AC and BD.
Proof: In ΔADC,
S and R are mid-point of AD and DC
∴ SR || AC and SR = \(\frac {1}{2}\) AC …….(1)
(A line segment joining the mid-points of two sides of a triangle is parallel to third and half of third side.)
Similarly in ΔABC,
PQ = AC and PQ = \(\frac {1}{2}\) AC …(2)
From eqn. (1) and (2),
PQ = SR
and PQ || SR
Hence ABCD is a parallelogram,
∠AOD = 90°
Now, diagonals of a rhombus bisect each other at 90°
∴ ∠EOF = 90°
⇒ ∠DFS = ∠EOF = 90° (Corresponding angles)
Again, SP || BD
∴ ∠ESF = ∠DFS (Alternates interior angles)
∴ ∠ESF = 90°
Hence PQRS is a rectangle.
![]()
Question 3.
ABCD is a rectangle and P, Q, R, and S are midpoints of the sides AB, BC, CD, and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: ABCD is a rectangle. P, Q R, and S are mid-points of AB, BC, CD, and DA respectively.
To Prove: Quadrilateral PQRS is a rhombus.
Construction: Join AC and BD.
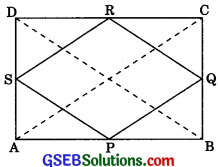
Proof: In ΔADC, S and R are the midpoints of AD and DC.
∴ SR || AC and SR = \(\frac {1}{2}\) AC …….(1)
(A line segment joining the mid-points of two sides of a triangle is parallel to third and half of the third side)
Similarly, in AABC,
PQ || AC
and PQ = \(\frac {1}{2}\) AC …….(2)
From eqn. (1) and (2),
PQ || SR and PQ = SR
∴ PQRS is a parallelogram.
Now, we know that the diagonals of a rectangle are equal.
∴ AC = BD ⇒ \(\frac {1}{2}\) AC = \(\frac {1}{2}\) BD
⇒ PQ = QR [From (1) and (2)]
∴PQRS is a rhombus.
![]()
Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal, and E is the mid-point of AB. A line is drawn through E parallel to AB intersecting BC at F (See figure). Show that F is the mid-point of BC.
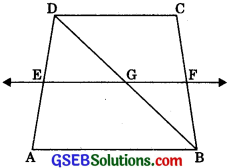
Solution:
To Prove: F is the mid-point of BC.
Proof: Let DB intersect EF at G.
In ΔDAB,
∴ E is the mid-point of DA and EG || AB.
∴ G is the mid-point of DB.
(A line drawn from mid-point of one side and parallel to another side, bisects the third)
Now in ΔDBC,
∴ G is the mid-point of DB. and GF || AB || DC
∴ F is the mid-point of BC.
(A line drawn from mid-point of one side and parallel to another side bisects the third side)
![]()
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. (See figure). Show that the line segments ALF and EC trisect the diagonal BD.
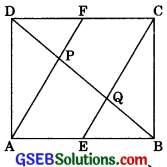
Solution:
To Prove: DP = PQ = BQ
Proof: AB || DC
and AB = DC
(Opposite sides of a parallelogram)
∴ \(\frac {1}{2}\) AB || \(\frac {1}{2}\) DC
and \(\frac {1}{2}\) AB = \(\frac {1}{2}\) DC (Dividing by 2 or both sides)
⇒ AE || FC (∴ E and Fare mid-points of AB and DC) AE = FC
Hence AECF is a parallelogram.
(If one pair of opposite sides of a quadrilateral are equal and parallel, then it is a parallelogram)
∴ AF || CE
(Opposite sides of a parallelogram)
Now in ΔDQC,
F is the mid-point and PF || QC.
∴ DP = PQ …….(1)
(A line drawn from mid-point of one side and parallel to other side bisects the third side of the triangle)
In ΔABP,
E is the mid-point of AB and EQ || AP.
∴ BQ = PQ …….(2)
(A line drawn from mid-point of one side and parallel to the other bisects the third side of the triangle)
Now from eqn. (1) and (2),
DP = PQ = BQ
Hence diagonal BD is trisected by AF and CE.
![]()
Question 6.
Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
Solution:
Given: A quadrilateral ABCD, in which P, Q, R and S are the mid-points of the sides AB, BC, DC and AD respectively.
To Prove: PR and QS bisect each other. Construction: Join PQ, QR, RS, SP, AC and BD.
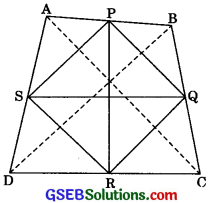
Proof: In AABD,
∴ P and S are mid-points of AB and AD respectively.
∴ PS || BD and PS = \(\frac {1}{2}\) BD ……(1)
2
(A line segment joining the mid-points of two sides parallel to the third side and half of it)
Similarly, we can show
QR || BD and QR = \(\frac {1}{2}\) BD ……(2)
From eqn. (1) and (2), we have
PS || QR
and PS = QR
If one pair of opposite sides of a quadrilateral is equal and parallel then it is a parallelogram Hence PQRS is a parallelogram.
Hence PR and QS are diagonals, therefore PR and Q§ bisect each other. (Diagonals of a parallelogram bisect each other).
![]()
Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallels to BC intersects AC at D. Show that
(i) D is the mid-point of AC.
(ii) MD⊥AC.
(iii) CM = MA = \(\frac {1}{2}\) AB.
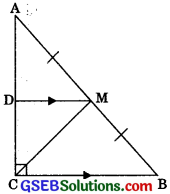
Solution:
(i) In ΔABC
M is the mid-point of AB and MD || BC.
∴ D is the mid-point of AC.
(A line drawn through mid-point of one side and parallel to other side bisects the third side)
(ii) DM || BC
∠MDC + ∠BCD = 180°
(Sum of consecutive interior angles is equal to 180°)
⇒ 90° +∠BCD = 180°
⇒ ∠BCD = 90°
∴ MD ⊥ AC
(iii) In ΔADM and ΔCDM,
AD = CD (Proved above)
∠ADM = ∠CDM (Proved above)
DM = DM (Common)
Hence, ΔADM = ΔCDM
(by SAS congruency)
∴ MA = CM (by CPCT)
M is the mid-point of AB.
∴ MA = CM = – AB
![]()