GSEB Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5 Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5

Question 1.
cos x . cos 2x . cos 3x
Solution:
Let y – cos x . cos 2.x . cos 3x.
Taking log of both sides, we get
log y = log (cos x . cos 2x . cos 3x)
= log cos x + log cos 2x + log cos 3x [Note : log_a mn = log_am + log_a n]
Differentiating both sides w.r.t. x,

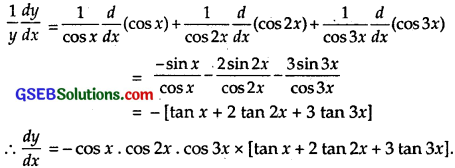
Question 2.
\(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Solution:
Let y = \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)
Taking log of both sides, we get

Question 3.
\((\log x)^{\cos x}\)
Solution:
Let y = \((\log x)^{\cos x}\)
Taking log of both sides, we get
log y = log (log x)^{cos x}
= cos x log (log x) [log mⁿ = n log m]
Differentiating both sides w.r.t. x,

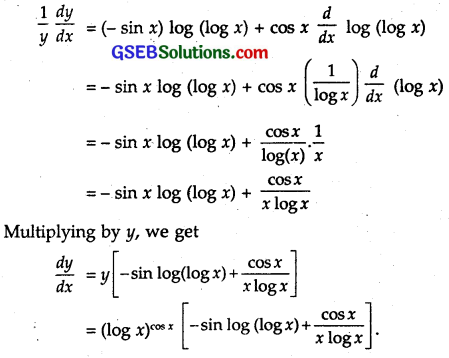
Question 4.
x^x – 2^{sin x}
Solution:
Let y = x^x – 2^{sin x}
= u – v.
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) – \(\frac { dv }{ dx }\).
Now, u = x² or log u = log x^{sin x} = x log x [ ∵ log m^{sin n} = n log m]
Differentiating w.r.t. x, we get
\(\frac { 1 }{ u }\) \(\frac { du }{ dx }\) = 1 . log x + x . \(\frac { 1 }{ x }\) = (1 + log x)
∴ \(\frac { du }{ dx }\) = u (1 + log x) = x^{sin x}(1 + log x).
Taking, v = 2^{sin x}, we get
∴ log v = log 2^{sin x} = sin x log 2
∴ \(\frac { 1 }{ v }\) \(\frac { dv }{ dx }\) = cos x log 2.
∴ \(\frac { dv }{ dx }\) = v cos x log 2 = 2^{sin x} cos x log 2.
∴ \(\frac { dv }{ dx }\) = \(\frac { du }{ dx }\) – \(\frac { dv }{ dx }\) = x^x (1 + log x) – 2^{sin x} cos x log 2.

Question 5.
(x + 3)² . (x + 4)³. (x + 5)⁴
Solution:
Let y = (x + 3)². (x + 4)³. (x + 5)⁴ .
Taking log of both sides, we get .
log y = log [(x + 3)².(x + 4)³.(x + 5)⁴]
= log (x + 3)² + log (x + 4)³ + log (x + 5)⁴ [log mn = log m + log n]
= 2 log (x + 3) + 3 log (x + 4) + 4 log (x + 5) [log mⁿ = n log m]
Differentiating both sides w.r.t. x,
\(\frac { 1 }{ y }\) \(\frac { dy }{ dx }\) = \(\frac { 2 }{ x+3 }\) + \(\frac { 3 }{ x+4 }\) + \(\frac { 4 }{ x+5 }\)
∴ \(\frac { dy }{ dx }\) = y(\(\frac { 2 }{ x+3 }\) + \(\frac { 3 }{ x+4 }\) + \(\frac { 4 }{ x+5 }\))
= (x + 3)² . (x + 4)³. (x + 5)⁴(\(\frac { 2 }{ x+3 }\) + \(\frac { 3 }{ x+4 }\) + \(\frac { 4 }{ x+5 }\))

Question 6.
\(\left(x+\frac{1}{x}\right)^{x}\) + \(x^{\left(1+\frac{1}{x}\right)}\)
Solution:
\(\left(x+\frac{1}{x}\right)^{x}\) + \(x^{\left(1+\frac{1}{x}\right)}\)
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = (x + \(\frac { 1 }{ x }\))^x .
Taking log both sides, we get

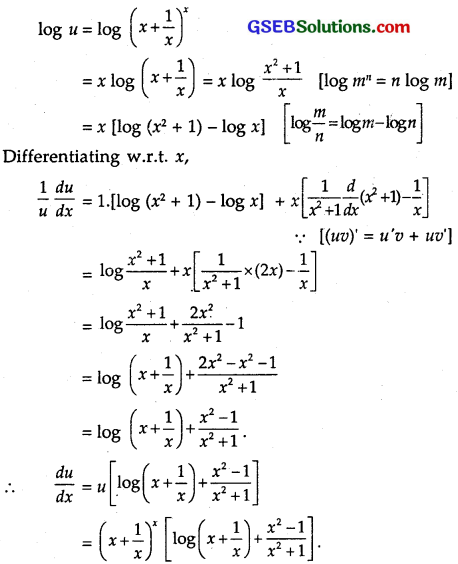
Now v = \(x^{\left(1+\frac{1}{x}\right)}\).
Taking log of both sides, we get
log v = log \(x^{\left(1+\frac{1}{x}\right)}\)
= (1 + \(\frac { 1 }{ x }\)) log x [log mⁿ = n log m]
Differentiating w.r.t. x,

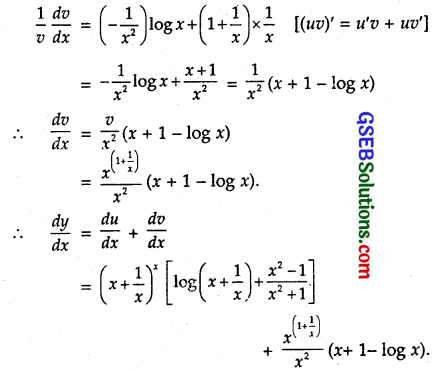
Question 7.
(logx)^x + x^{log x}
Solution:
Let y = (logx)^x + x^{log x}
= u + v
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = (log x)^x.
Taking log both sides, we get
log v = log (log x)^x
= x log (log x) [log mⁿ = n log m]
Differentiating w.r.t. x,

Now, v = x^{log x}.
Taking log of both sides, we get
log v = log x^{log x} [log mⁿ = n log m]
= log x . log x = (log x)²
Differentiating w.r.t. x,

Question 8.
(sin x)^x + sin^-1\(\sqrt{x}\)
Solution:
Let y = (sin x)^x + sin^-1\(\sqrt{x}\)
= u + v
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = (sin x)^x.
Taking log both sides, we get
log u = log (sin x)^x
= x log (sin x) [log mⁿ = n log m]
Differentiating w.r.t. x,

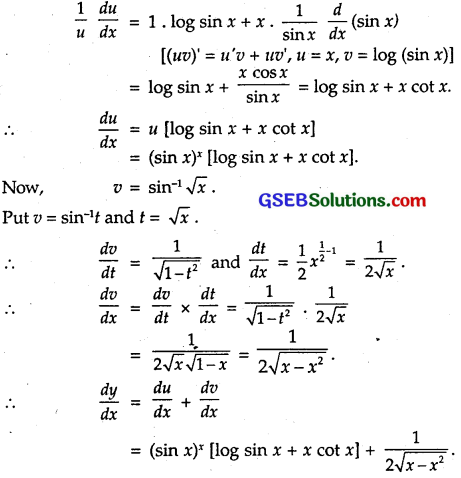
Question 9.
x^{sin x} + (sin x)^{cos x}
Solution:
Let y = x^{sin x} + (sin x)^{cos x}
= u + v
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = x^x.
Taking log both sides, we get
log u = log x^x [log mⁿ = n log m]
= sin x log x
Differentiating w.r.t. x,

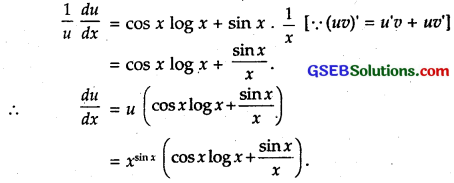
Now, u = (sin x)^{cos x}.
Taking log both sides, we get
log v = log (sin x)^{cos x} [log mⁿ = n log m]
Differentiating w.r.t. x,

Question 10.
x^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\)
Solution:
Let y = x^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\)
= u + v
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = x^{x cos x}.
Taking log both sides, we get
log u = log x^{x cos x}
= x cos x log x [log mⁿ = n log m]
Differentiating w.r.t. x,

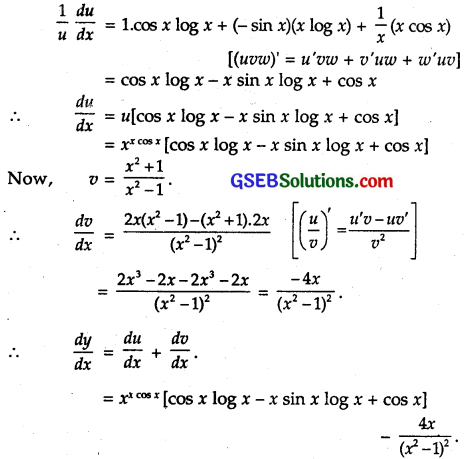
Question 11.
(x cos x)^x + (x sin x)^{\(\frac{1} {x}\)}
Solution:
Let y = (x cos x)^x + (x sin x)[^{\(\frac{1} {x}\)}
= u + v
∴ \(\frac { dy }{ dx }\) = \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\).
Now, u = (x cos x)^x.
Taking log both sides, we get
log u = log (x cos x)^x
= x log (x cos x) [log mⁿ = n log m]
= x (log x + log cos x)
Differentiating w.r.t. x,

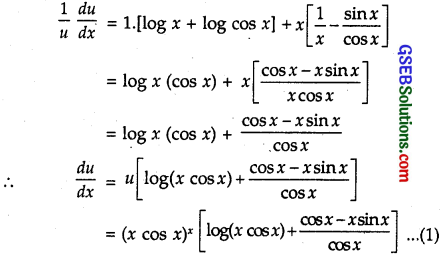
Further, v = (x sinx)^{\(\frac{1} {x}\)}.
Taking log of both sides, we get
log v = log (x sinx)^{\(\frac{1} {x}\)}
= \(\frac{1} {x}\) log (x sin x) [log mⁿ = n log m]
= \(\frac{1} {x}\) (log x + log sin x)
Differentiating both sides,

Question 12.
x^y + y^x = 1
Solution:
Let y = x^y + y^x = 1
Let u = x^y and u = y^x
∴ u + v = 1
or \(\frac { du }{ dx }\) + \(\frac { dv }{ dx }\) = 0. … (1)
Now, u = x^y.
Taking log both sides, we get
log u = log x^y
= y log x [log mⁿ = n log m]
Differentiating w.r.t. x,

Question 13.
y^x = x^y
Solution:
y^x = x^y
Taking log both sides, we get
x log y = y log x [log mⁿ = n log m]
Differentiating w.r.t. x,

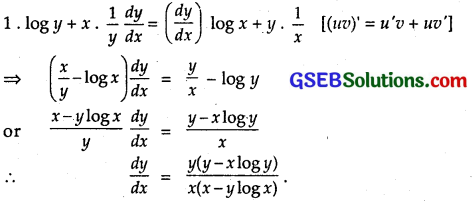
Question 14.
(cos x)^y = (cos y)^x
Solution:
(cos x)^y = (cos y)^x
Taking log both sides, we get
y log (cos x) = x log cos y [log mⁿ = n log m]
Differentiating w.r.t. x,

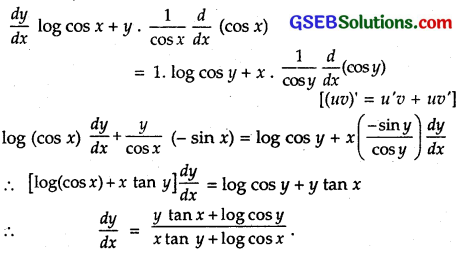
Question 15.
xy = e^x-y
Solution:
xy = e^x-y
Taking log both sides, we get
log x + log y = (x – y) log e [log xy = log x + log y]
= (x – y) [ log_e = 1]
Differentiating w.r.t. x,
\(\frac { 1 }{ x }\) + \(\frac { 1 }{ y }\)\(\frac { dy }{ dx }\) = 1 – \(\frac { dy }{ dx }\)
⇒ (\(\frac { 1 }{ y }\) + 1)\(\frac { dy }{ dx }\) = 1 – \(\frac { 1 }{ x }\) = \(\frac { x-1 }{ x }\)
∴ \(\frac { dy }{ dx }\) = \(\frac { y(x-1) }{ x(y+1) }\)

Question 16.
Find the derivatives of the functions given by
f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸) and hence find f’ (1).
Solution:
Let y = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸)
Taking log of both sides, we get
log y = log(1 + x) (1 + x²) + log(1 + x²) + log(1 + x⁴) + log(1 + x⁸)
Differentiating w.r.t. x,

Question 17.
Differentiate (x² – 5x + 8)(x² + 7x + 9) in three ways mentioned below?
(i) by using product rule.
(ii) by expanding the product to obtain a single polynomial.
(iii) by logarithmic differentiation.
Do they all give the same answer?
Solution:
Method (i) : (uv)’ = u’v + uv’
Let y = (x² -5x + 8)(x³ + 7x + 9)
Differentiating by product rule, we get
\(\frac { dy }{ dx }\) = [ \(\frac { d }{ dx }\)(x² -5x + 8) ] (x³ + 7x + 9) + (x² – 5x + 8) x \(\frac { d }{ dx }\) (x³ + 7x + 9)
= (2x – 5) (x³ + 7x + 9) + (x² – 5x + 8) (3x² + 7)
= 2x(x³ + 7x + 9) – 5(x³ + 7x + 9) + 3x²(x² – 5x + 8) + 7(x² – 5x + 8)
= 5x⁴ – 20x³ + 45x² – 52x + 11.

Method (ii) : y = (x² – 5x + 8) (x³ + 7x + 9)
= x² (x³ + 7x + 9) – 5x (x³ + 7x + 9) + 8 (x³ + 7x + 9)
= x⁵ – 5x⁴ + 15x³ – 26x² + 11 x + 72
\(\frac { dy }{ dx }\) = 5x⁴ – 20x³ + 45x² – 52 x + 11.

Method (iii) : y = (x² – 5x + 8) (x³ + 7x + 9)
Taking log of both sides, we get
log y = log (x² – 5x + 8) + log (x³ + 7x + 9) [log mn = log m + log n]
Differentiating w.r.t. x,

[See part (ii) for simplification] Obviously, the answer is the same in all the three cases.

Question 18.
If u, v and w are functions of x, then show that \(\frac { d }{ dx }\)(u . v . w) = \(\frac { du }{ dx }\) . v . w + u . \(\frac { dv }{ dx }\) . w + u . v . \(\frac { dw }{ dx }\) in two ways : first by repeated application of product rule and secondly by logarithmic differentiation.
Solution:
Let y = u .v . w = u . (vw)
(i) Differentiating both sides we get